Методы моделирования (корреляционно-регрессионный анализ)
По предоставленным исходным данным необходимо:
- На исходном массиве данных построить матрицу парных коэффициентов корреляции;
- Проверить значимость каждого из коэффициентов на уровне значимости a = 0,05;
- Определить признаки, наиболее важные для объяснения вариации исследуемой переменной.
- Построить линейное уравнение регрессии между исследуемой переменной и выбранными признаками, предварительно проверив этот набор признаков на наличие мультиколлинеарности и сделать соответствующие корректировки при необходимости;
- Используя критерий Фишера, проверить на уровне a=0,05 значимость уравнения регрессии.
- В значимом уравнении регрессии определить значимость коэффициентов уравнения. Если в модели есть незначимые коэффициенты, то путем пошагового исключения незначимых факторов построить уравнение со всеми значимыми коэффициентами.
- Выписать итоговое уравнение регрессии и дать экономическую интерпретацию полученного уравнения.
Ход работы
С помощью пакета «Корреляция» надстройки «Анализ данных» MS Excel построим матрицу парных коэффициентов корреляции (Лист «Корреляция»):
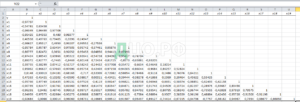
Рис. 1. Общий вид матрицы парных коэффициентов корреляции
Проверим значимость каждого из коэффициентов парной корреляции на уровне значимости . Для этого выдвинем гипотезе о равенстве 0 соответствующего коэффициента корреляции и найдем наблюдаемое соответствующее значение статистики по формуле для каждой пары факторов (Матрица наблюдаемых значений t—критерия). Сравним найденные значения с критическим значением Стьюдента на уровне значимости и для степеней свободы.
Если , то гипотезу отклоняем и можем говорить о значимости соответствующего коэффициента корреляции. Если , то коэффициент корреляции близок к 0, и можно говорить о статистической независимости исследуемых факторов. Если коэффициент значим, то соответствующей ячейке Матрицы значимости присвоим значение 1, иначе 0:
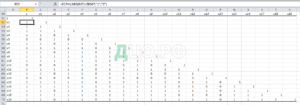
Наиболее важными объясняющими признаками будут те признаки, у которых коэффициент корреляции наибольший.
Построим уравнение регрессии между исследуемой переменной и выбранными признаками. Предварительно проверим этот набор признаков на наличие мультиколлинеарности. Признаки и признаются коллинеарными, если . Группы коллинеарных признаков выделим цветами в корреляционной матрице. Все признаки, указанные в пункте 3 являются попарно коллинеарными.
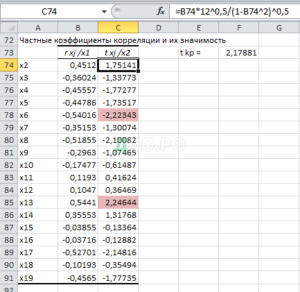
То есть выявлена целесообразность включения в модель регрессии (при условии, что фактор уже включен) только факторов. Следовательно, если в модель присутствует переменная , то переменную включать нецелесообразно.
При неизменном уровне экономической активности населения в среднем за год и увеличении среднемесячных номинальных начислений заработной платы работников организаций на 1 тыс. руб. сбросы загрязнений сточных вод в поверхностные водные объекты уменьшится в среднем на 0,061 тыс. куб. м.
Прикрепленные файлы: |
|
|---|---|

|
Администрация сайта не рекомендует использовать бесплатные работы для сдачи преподавателю. Эти работы могут не пройти проверку на уникальность. Узнайте стоимость уникальной работы, заполните форму ниже: Узнать стоимость |

|
Скачать файлы: |
|
|
|
