Курсовая работа на тему «Математическое моделирование»

Введение
1. Теоретические основы математического моделирования
1.1. Сущность математического моделирования
1.2. Дифференциальные уравнения как основа математической модели
1.3. Основы составления модели путем использования уравнений
1.3.1. Уравнения в дифференциалах
1.3.2. Уравнения в производных
1.3.3. Простейшие интегральные уравнения
2. Анализ областей математического моделирования
2.1.Эффективность рекламы
2.2.Спрос и предложение
2.3. Дифференциальные модели в экологии
2.4.Модели физических процессов
Заключение
Список литературы

Введение

Актуальность темы курсовой работы «Математическое моделирование» заключается в том, что понятия, которые созданы современной математикой, кажутся очень далекими от реального мира. Но следует отметить, что именно благодаря им люди смогли оценить ход космических кораблей, раскрыть загадки структуры атомного ядра, создать технический мир, который стал основанием современного производства. Опыт и эксперимент представляют собой основные методы изучения природы. Проведение экспериментов дало толчок для установления многих законов природы. Но не всегда проведение эксперимента оправдывает цели. За последние годы в самых разнообразных сферах науки и техники роль методов математического моделирования увеличивается.
Изучая явления природы и решая задачи физики и техники, химии и биологии, других наук, не всегда представляется возможным сразу установить прямую связь между величинами, характеризующими различные эволюционные процессы. Но во многих случаях возможно определить связь между величинами (функциями) и скоростями их изменения относительно других (независимых) переменных величин, т.е. составить уравнения, в которых искомые функции находятся под знаком производной. Эти уравнения называются дифференциальными.
Дифференциальное уравнение, которое получили в процессе изучения какого-то реального явления, называют дифференциальной моделью этого явления. Дифференциальные модели — это частный случай того множества математических моделей, построенных в ходе познания внешнего мира.
Цель данной курсовой работы: изучить математические модели, которые основаны на различных процессах, таких как модель рекламной компании, спроса и предложения, моделей в экологии, моделей процессов физики: кривая погони, атмосферное давление.
Задачи:
изучить и проанализировать литературу по данной теме;
выделить основные термины, касающиеся математического моделирования и решения прикладных задач;
изучить влияние математического моделирования на реальные процессы.
Курсовая работа состоит из введения, двух разделов, заключения и списка литературы. В первом разделе освещаются основные определения и понятия математического моделирования и дифференциальных уравнений. Во втором разделе рассматривается прикладное применение математического моделирования к реальным процессам с помощью дифференциальных уравнений на конкретных примерах.

Теоретические основы математического моделирования

1.1. Сущность математического моделирования

Термин математическая модель означает приближенное описание некоторой группы явлений окружающего мира, которое выражается посредством математической символики.
Говоря о математической модели, необходимо подчеркнуть, что объект-заместитель и объект-оригинал – это объекты различной природы, которые отличаются друг от друга как грузик, который колеблется на пружине, от дифференциального уравнения, описывающего эти гармонические колебания.[8] Моделирование – это замена одного объекта (оригинала) другим (моделью) и установление или исследование свойств оригинала в процессе исследования свойств модели. Замещение производится в целях упрощения, удешевления, ускорения фиксации или изучения свойств оригинала.
В общем случае объектом-оригиналом может быть любая естественная или искусственная, реальная или воображаемая система.
Разнородные задачи теоретических и прикладных вариантов, содержащие элементы “движения”, дают построение математических моделей в виде уравнений, в которые, помимо независимых переменных и неизвестных функций, входят ещё и производные (или дифференциалы) от искомых функций. Таким образом, данные уравнения можно называть дифференциальными уравнениями.
Такие модели, показанные в виде дифференциальных уравнений, называют динамическими математическими моделями, которые описывают реальные объекты. В этих моделях имеются и их производные (скорости, ускорения и т.п.). Математические соотношения между независимыми переменными и функциями определяют как кинематические модели.
Продуктивность динамического моделирования реальных процессов реализуется в относительной простоте. Кинематические модели дают возможность наиболее полно изучить рассматриваемые объекты, поэтому и являются завершающим шагом их изучения. Следовательно, можно прийти к выводу, что создание динамической модели (дифференциального уравнения) представляет собой не конкретную цель, а лишь переходное звено от объекта изучения к его кинематической модели. Расшифровка динамической модели, т. е. переход её в кинематическую, называется интегрированием динамической модели или, как точнее выразиться, интегрированием дифференциального уравнения. Углубляясь в этот вопрос, можно рассматривать достаточное множество результативных приемов как точного, так и приближенного интегрирования дифференциальных уравнений. Поэтому продуктивность динамического моделирования заключается в том, что оно позволяет алгоритмизировать процесс организации кинематической модели объекта изучения, а точнее, сконструировать структуру определенных правил (алгоритм) организации кинематической модели исследования. Из этого становится очевидно значение задачи о методах решения дифференциальных уравнений. Т.к. кинематическая модель задачи служит для исследования свойств объекта её изучения, то вместо задачи интегрирования дифференциальных уравнений появляется задача определения свойств уравнений и их решений.
В динамических моделях значение y(t) зависит от всего прошлого (предыстории) входного процесса:
y(t)=F(u(s),s≤t) (1)
Динамические модели позволяют выделить наличие «памяти», инерционности системы. Математический аппарат представления динамических систем есть дифференциальные, разностные уравнения, конечные автоматы, случайные процессы.
Эти две задачи – разработка методов интегрирования дифференциальных уравнений и изучение различных свойств их решений – составная часть теории дифференциальных уравнений как самостоятельный раздел математики. Метод же теории дифференциальных уравнений в общем образует аппарат математического анализа. Интегральное исчисление функции одной переменной, по сути, — теория интегрирования дифференциальных уравнений вида y^’=f(x). В самом деле, y=∫▒〖f(x)dx〗,y=F(x)+C – одно параметрическое семейство кривых (где F^’ (x)=f(x)).

1.2. Дифференциальные уравнения как основа составления модели

Дифференциальным уравнением называется соотношение
F(x,y,y^’,…,y^((n) ) )=C, (2)
связывающее значения независимого переменного x с искомой функцией y=y(x) и ее производных до некоторого порядка n≥1. Порядок n старшей производной, входящей в уравнение, называется порядком уравнения. Подразумевается, что в (2) значения y,y’,…,y^((n)) берутся при одном и том же x.
Решением уравнения (2) называется функция, которая определяется на некотором интервале (или отрезке), имеющая производные до порядка n и удовлетворяющая этому уравнению, то есть при подстановке ее в уравнение обращающая его в тождество на этом интервале [18], т.е.
F(x,y,y^’,…,y^((n) ) )=0,∀x∈(a,b)
Способ определения решений называется интегрированием дифференциальных уравнений. График решений дифференциального уравнения носит название интегральной кривой данного уравнения.
Общим решением дифференциального уравнения n-го порядка называют функцию вида:
y=φ(x,c_1,c_2,…,c_n ) (3)
которая является решением уравнения и содержит столько произвольных постоянных c_1,c_2,…,c_n, каков порядок этого уравнения. Функцию, которая записана в неявном виде,
ψ(x,y,c_1,c_2,…,c_n )=0 (4)
называют общим интегралом дифференциального уравнения.
Частное решение дифференциального уравнения – это решение, получаемое из общего решения (3) при заданном выборе значений произвольных постоянных c_1,c_2,…,c_n.
Задачей Коши для некоторых дифференциальных уравнений называют задачу вычисления частного решения этого уравнения, которое удовлетворяет заданным начальным условиям.
Зависимость, полученная из общего интеграла (4) при определенных значениях произвольных постоянных c_1,c_2,…,c_n, называют частным интегралом дифференциального уравнения (2).
Если в (2) n = 1, то имеем обыкновенное дифференциальное уравнение первого порядка F(x,y,y^’ )=0. В большинстве случаев его можно записать в виде
dy/dx=f(x,y)
Тогда его называют обыкновенным дифференциальным уравнением первого порядка, которое разрешено относительно производной. При n > 1 имеем обыкновенное дифференциальное уравнение высшего порядка.
Например:
а) y^’+xy=3x^2 – обыкновенное дифференциальное уравнение первого порядка первой степени;
б) 〖(y^’)〗^4+2xy^’+8xy=0 – обыкновенное дифференциальное уравнение первого порядка четвертой степени;
в) (d^3 y)/(dx^3 )-dy/dx+5 (d^2 y)/(dx^2 )=0 – обыкновенное дифференциальное уравнение третьего порядка первой степени;
г) — обыкновенное дифференциальное уравнение первого порядка первой степени;
5) xd^2 y-dydx=e^x dx^2 – обыкновенное дифференциальное уравнение второго порядка первой степени;
д) a ∂u/∂x+b ∂u/∂y=1 – дифференциальное уравнение в частных производных первого порядка;
е) (∂^2 u)/∂x∂y=x ∂u/∂y-y ∂u/∂x – дифференциальное уравнение в частных производных второго порядка.

1.2. Основы составления модели путем использования уравнений.

Схема построения дифференциальных уравнений по условию задачи включает в себя нахождение зависимости между переменными величинами и их приращениями. При этом чаще всего самое главную роль имеет понимание законов той сферы науки, с коей связана природа рассматриваемой задачи. Так, например, в механике это могут быть законы Ньютона, в теории электрических цепей – законы Кирхгофа и т.д. Всеобщего метода образования дифференциальных уравнений, подходящего для всех случаев, назвать нельзя. Можно дать лишь некоторые общие рекомендации. Во многих случаях методика решения прикладных задач на составление дифференциальных уравнений заключается в следующем:
а) крайне внимательно разобрать условия задачи и правильно составить чертеж;
б) верно получить дифференциальное уравнение рассматриваемого процесса;
в) выполнить интегрирование составленного дифференциального уравнения, определить общий род его решения;
г) установить частное решение задачи на основании обозначенных начальных условий;
д) прийти к нахождению вспомогательных параметров (для этого используются дополнительные условия задачи);
е) сделать вывод общего закона изучаемого процесса и нахождению числовых значений величин, которые необходимо найти;
ж) дать анализ ответу и правильно выполнить проверку исходного положения задачи.
При формировании дифференциальных уравнений 1-го порядка из условия геометрической или физической задачи как правило приходят к одному из обозначенных трёх видов уравнений:
1) дифференциальному уравнению в дифференциалах;
2) дифференциальному уравнению в производных;
3) простейшему интегральному уравнению с последующим преобразованием его в дифференциальное уравнение.
Рассмотрим составление уравнения каждого из приведенных форм по отдельности.

1.2.1. Уравнения в дифференциалах

При образовании дифференциальных уравнений 1-го порядка во многих случаях бывает целесообразно использовать так называемый метод дифференциалов. Его суть заключается в том, что из условия задачи приближенным путём составляются зависимости между дифференциалами (приращениями). При этом используются допущения, которые упрощают задачу, и, вместе с этим, не отражаются на результатах: малые приращения величин замещаются их дифференциалами; непостоянно текущие физические процессы (неравномерное движение точки, нагревание или охлаждение тела, истечение жидкости из сосуда и т. д.) на протяжении небольшого промежутка времени dt считаются как равномерные и протекающие с постоянной скоростью. Эти предположения не отображаются на справедливости конечных результатов вследствие того, что изменение приращений дифференциалами заключается в отбрасывании бесконечно малых высших порядков малости. Так как отношение дифференциалов функции и аргумента – это предел отношения их приращений, то сообразно тому, как приращения стремятся к нулю, допущения выполняются с большей точностью. Полученные при этом дифференциальные уравнения являются точными, если они однородны и линейны в отношении дифференциалов.

1.2.2. Уравнения в производных

В некоторых случаях можно получить дифференциальные уравнения, содержащие вместо дифференциалов производные, которые рассматриваются как скорости изменения величин. В этом случае, судя по всему, мы не рассматриваем приращения, но они приняты предварительно. А именно, полагая скорость как v=ds/dt, не пишем Δs и Δt, хотя эти приращения в сущности учтены, т. к.
v=ds/dt=lim┬(Δt→0)⁡〖Δs/Δt〗
Таким же образом ускорение в момент времени t выражается зависимостью:
a=(d^2 s)/(dt^2 )=dv/dt=dv/ds∙ds/dt=dv/dt∙v

1.2.3. Простейшие интегральные уравнения

Решение некоторых задач приводит к уравнениям, которые содержат неизвестные функции под знаком интеграла. Такие уравнения называют интегральными. Они, в частности, проявляются в составлении уравнения с использованием геометрического смысла определённого интеграла как площади криволинейной трапеции и другие интегральные формулы (длина дуги, площадь поверхности, объем тела, работа силы и т. д.). В простейших случаях путём дифференцирования удается преобразовать интегральные уравнения в дифференциальные, которые интегрируются обычными методами.

2. Анализ областей математического моделирования

2.1.Эффективность рекламы

В начале рекламы фирмой нового продукта или услуги прибыль от будущих продаж будет более чем покрывать расходы на дорогую кампанию или затраты могут превысить прибыль, поскольку только небольшая часть возможных покупателей будет проинформирована о новом продукте. Затем, когда количество продаж заметно возрастет, можно будет рассчитать прибыль, и, наконец, когда рынок заполнится, будет бессмысленно рекламировать продукт.
Предположим, что торговая организация продает продукт B, о котором в момент времени t знает x покупателей из определенного числа потенциальных покупателей N. Мы также предполагаем, что для увеличения продаж товаров B рекламные объявления были размещены на радио и телевидении. Следующая информация распространяется среди клиентов через общение друг с другом. Можно отметить, что после рекламы скорость изменения числа тех, кто знает о продукте B, пропорциональна как количеству потребителей, которые знают о продукте, так и количеству потребителей, которые не знают о нем.
Если вести отсчет времени после рекламных объявлений, когда о товаре узнало N⁄γ человек, то приходим к дифференциальному уравнению
dx/dt=kx(N-x)(5)
с начальными условиями (x=N)⁄γ при t=0. В уравнении (5) коэффициент k – это положительный коэффициент пропорциональности. Интегрируя уравнение (5), находим, что
1/N ln⁡〖x/(N-x)=kt+C〗.
Полагая NC=C_1, приходим к равенству
x/(N-x)=Ae^Nkt,где A=e^(C_1 ).
Если последнее уравнение разрешить относительно x, то получим соотношение
x=N (Ae^Nkt)/(Ae^Nkt+1)=N/(1+Pe^(-Nkt) ) (6)
где P=1⁄A.
В экономической литературе уравнение (6) обычно называют логистической кривой.
Учитывая начальные условия, переписываем уравнение (6) в виде
x=N/(1+(γ-1)e^(-Nkt) ).[2]

2.2.Спрос и предложение

Спрос и предложение – экономические категории товарного производства, которые возникают и функционируют на рынке, в сфере товарного обмена. При этом спрос – представленная на рынке потребность в товарах, а предложение – продукт, имеющийся на рынке или доставленный на него. Одним из экономических законов товарного производства является закон спроса и предложения, заключающийся в единстве спроса и предложения и их объективном стремлении к соответствию.
Рассмотрим следующую задачу. Пусть дана модель рынка с прогнозируемыми ценами. В простых моделях рынка зависимость спроса и предложения обозначают от текущей цены на товар. Однако спрос и предложение в реальных ситуациях зависят еще и от характера ценообразования и скорости изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и второй производными функции цены P(t).
Пусть функции спроса D и предложения S зависят от цены Р и ее производных:
D(t)=3P^»-P^’-2P+18,
S(t)=4P^»+P^’-3P+3 (7)
Принятые зависимости довольно реалистичны: покажем это на слагаемых с производными функции цены.
1. Спрос «подогревается» скоростью изменения цены: если цена увеличивается (P^»>0), тогда рынок поднимает интерес к продукту, и наоборот. Наращивание темпов роста цены отпугивает покупателя, следовательно, слагаемое с первой производной функции цены входит со знаком минус.
2. Предложение в еще большей мере усиливается ростом цен, поэтому коэффициент при P^» в функции S(t) больше, чем в D(t). Увеличение цены также наращивает предложе¬ние, потому слагаемое, содержащее P’, входит в выражение для S(t) со знаком плюс.
Необходимо выяснить зависимость цены от времени. Так как равновесие рынка характеризуется равен¬ством D=S, приравняем правые части уравнений (7). После приведения подобных, получаем
P^»+2P^’+5P=15 (8)
Соотношение (8) представляет линейное неоднородное дифференциальное уравнение второго порядка относительно функции P(t). Общее решение такого уравнения состоит из суммы какого-либо его частного решения и общего решения соответствующего однородного уравнения
P^»+2P^’+5P=0 (9)
Характеристическое уравнение имеет вид
k^2+2k+5=0
Его корни — комплексно-сопряженные числа: k_1,2=-1±2i, значит, общее решение уравнения (9) дается фор¬мулой
¯P (t)=e^(-t) (C_1 cos⁡2t+C_2 sin⁡2t)
где C_1 и C_2 — произвольные постоянные. Пусть частное решение неоднородного уравнения (8) Р = P_st – постоянная величину в качестве установившейся цену. Подстановка в уравнение дает значение P_st:
P_st=3
Таким образом, общее решение уравнения (8) имеет вид
P(t)=3+e^(-t) (C_1 cos⁡2t+C_2 sin⁡2t ) (10)
Замечаем, что P(t)→P_st=3 при t→∞, т.е. все интегральные кривые имеют горизонтальную асимптоту Р = 3 и колеблются около нее. Следовательно, все цены стремятся к установившейся цене P_st с колебаниями около нее, при этом амплитуда этих колебаний затухает со временем.
Приведем частные решения этой задачи в двух вариантах: задача Коши и смешанная задача.
1. Задача Коши. Пусть в начальный момент времени известна цена, а также тенденция ее изменения:
t=0;P=4,P^’=1
Подставляя первое условие в формулу (10), получаем P(0) = C_1 + 3 = 4, откуда C_1=1, т.е. имеем
P(t)=3+e^(-t) (cos⁡2t+C_2 sin⁡2t ) (11)
Дифференцируя, имеем отсюда
P^’ (t)=e^(-t) [(2C_2-1) cos⁡2t-(C_2+2) sin⁡2t] Теперь реализуем второе условие задачи Коши: P^’ (0)=2C_2-1=1, откуда C_2=1. Окончательно получаем, что решение задачи Коши имеет вид
P(t)=3+e^(-t) (cos⁡2t+sin⁡2t )
или, в более удобной форме:
P(t)=3+√2 e^(-t) cos⁡〖(2t-π⁄4)〗

Рис.1

2. Смешанная задача. Пусть в начальный момент времени известны цена и спрос: t=0;P=4,D=16.
Так как первое начальное условие такое же, как и в преды¬дущем пункте, то имеем и здесь решение (11). Так как производные функции Р(t) выражаются формулами
P^’ (t)=e^(-t) [(2C_2-1) cos⁡2t-(C_2+2) sin⁡2t ],
P^» (t)=e^(-t) [(4C_2+3) cos⁡2t-(3C_2-5) sin⁡2t] Отсюда P^’ (0)=2C_2-1 и P^» (0)=-4C_2-3. Подставим эти равенства во второе условие задачи, т.е. D(0) = 16, получим с учетом вида D(t) из первой формулы (7): C_2=-1. Итак, решение данной задачи имеет вид
P(t)=3+e^(-t) (cos⁡2t+sin⁡2t )
или в более удобной форме:
P(t)=3-√2 e^(-t) sin⁡(2t-π⁄4) (12)
Интегральные кривые, соответствующие задачам 1 и 2, изоб-ражены на рис. 1.

2.3.Дифференциальные модели в экологии

Рассмотрим дифференциальные модели популяций, которые характеризуются размножением или вымиранием последних, а также сосуществованием различных видов животных в ситуации «хищник – жертва».
Пусть x(t) – число особей в популяции в момент времени t. Тогда если A – число особей в популяции, рождающихся в единицу времени, а B – число особей, умирающих в единицу времени, то с достаточным основанием можно утверждать, что скорость изменения x со временем задается формулой
dx/dt=A-B (13)
Задача теперь состоит в том, чтобы описать зависимость A и B от x. Простейшим случаем является ситуация, когда
A=ax,B=bx,(14)
где a и b – коэффициенты рождения и смерти особей в единицу времени соответственно. С учетом равенств (14) дифференциальное уравнение (13) перепишется в виде
dx/dt=(a-b)x (15)
Полагая, что в момент времени t=t_0 число особей в популяции есть x=x_0, из уравнения (15) находим
x(t)=x_0 e^((a-b)(t-t_0)).
Из полученного равенства следует, что a>b, то при t→∞ число особей x→∞. С другой стороны, если a<b, то x→0 при t→∞ и популяция становится вымирающей.
Хотя приведенная модель является упрощенной, она в ряде случаев соответствует действительности. Практически же все модели, которые описывают реальные процессы и явления, нелинейны, и вместо дифференциального уравнения (5) следует рассматривать уравнение вида
dx/dt=f(x),
где f(x) – нелинейная функция, например, уравнение вида
dx/dt=f(x)=ax-bx^2,
где a>0,b>0.
Полагая, что x=x_0 при t=t_0 из последнего уравнения находим, что
x(t)=(x_0 a/b)/(x_0+[a⁄b-x_0]e^(-a(t-t_0)) ) (16)
Отсюда видно, что при t→∞ число особей в популяции x(t)→a/b. При этом возможны два случая: a⁄b>x_0 и a⁄b<x_0.
Соотношение (16) описывает, в частности, популяции фруктовых вредителей и некоторых видов бактерий.
Решим следующую задачу.
В подходящей для размножения среде находится некоторое количество N_0 бактерий. Необходимо выявить соотношение роста числа бактерий с течением времени.
Пусть N(t) – количество размножающихся бактерий в момент времени t: N(0)=N_0. Полагаем, что N(t) меняется во времени непрерывно дифференцируемо. Тогда скорость размножения есть производная от функции N(t); следовательно, отмеченный в условии задачи биологический экспериментальный закон способствует составлению дифференциального уравнения размножения бактерий:
(dN(t))/dt=kN(t),k>0 (17)
Коэффициент k обусловливается видом бактерий и средой, в которой они находятся, и определяется экспериментально.
Таким образом, задача представлена чисто математической задачей: найти решение N=N(t) уравнения (17), для которого N(0)=N_0.
Так как N(t)>0, то разделив обе части уравнения (17) на N(t), получим
d/dt (ln⁡N(t) )=k
Отсюда
ln⁡〖N(t)〗=kt+C_1 (18)
где C_1 – произвольная постоянная; обозначим ее так: C_1=ln⁡C,C>0. Из (18) имеем
N(t)=Ce^kt (19)
Чтобы из множества функций (19) выделить функцию, описывающую процесс размножения бактерий, используем условие N(0)=N_0, откуда N_0=C. Окончательно получим
N(t)=N_0 e^kt (20)
Т.е. численность бактерий возрастает по показательному закону.[15] Рассмотрим модель взаимосвязи по принципу «хищник—жертва», которая была В. Вольтерром. Предположим существование системы, которая состоит из двух видов, и один вид поедает другой.
Рассмотрим случай, когда один из видов является хищником численностью y, а другой – жертвой, число которых x, и будем считать, что хищник питается только жертвой.
Если рождаемость жертв превышает их смертность, e>0, то их убыль пропорциональна вероятности встречи жертвы с хищником, т.е. пропорциональна произведению численностей x∙y.
Помимо этого, присутствует процесс естественной смертности хищников, причем скорость смертности пропорциональна их количеству.
Тогда динамика численности популяций в системе хищник – жертва будет представляться системой дифференциальных уравнений:
{█(dx/dt=x(ε_x-γ_xy y)@dy/dt=-y(ε_x-γ_xy x) ) (21)┤
Система имеет равновесное решение:
¯x=ε_y/γ_x ,¯y=ε_x/γ_y
Так как все коэффициенты ε_x,ε_y,γ_x,γ_y положительны и постоянны, точка (¯x,¯y) расположена в положительном квадранте фазовой плоскости. Линеаризация системы вблизи этой точки дает:
{█(dξ/dt=-(ε_y γ_y)/γ_x @dη/dt=-(ε_x γ_x)/γ_y ) (22)┤

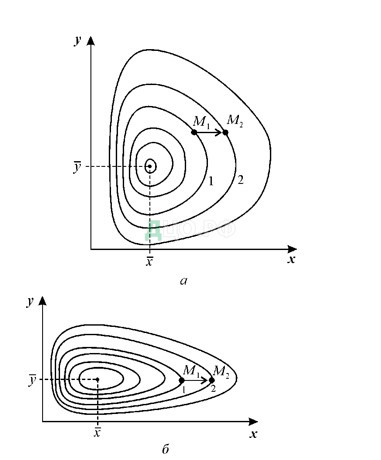
Рис. 2. Фазовый портрет системы 17. Особая точка типа «центр».
а – параметры системы: e_x = 4,g_xy= 0,3,e_y = g_yx= 0,4
б – параметры системы: e_x = 2,g_xy= 0,3,e_y = g_yx= 0,4
Здесь x, h — отклонения ¯x,¯y численностей от их стационарных значений:
ξ(t)=x(t)-¯x
η(t)=y(t)-¯y
Характеристическое уравнение системы (18):
|■(-λ&-(ε_y γ_y)/γ_x @-(ε_x γ_x)/γ_y &-λ)|=0; λ^2+ε_x ε_y=0
Корни этого уравнения чисто мнимые:
λ_1,2=±√(ε_x ε_y )
Таким образом, оценка устойчивости состояния равновесия по отношению к малым возмущениям показала, что особая точка представляется «нейтрально» устойчивой (типа «центр»), т. е. всякие отклонения от равновесия не затухают, но приводят систему в колебательный режим с амплитудой, которая зависит от величины возмущения. Траектории системы на фазовой плоскости представляют собой замкнутые кривые, которые расположены на разных расстояниях от точки равновесия (рис. 2).
Изменения численности жертвы и хищника во времени представляют собой колебания, при этом колебания численности хищника отстают по фазе от колебаний жертв.
Особая точка типа центр устойчива по Ляпунову, но не асимптотически. Представим на примере, как это проявляется. Пусть колебания x(t) и y(t) возникают таким образом, что изображающая точка движется по фазовой траектории 1 (рис 2).
В момент нахождения точки в положении M_1, к системе присоединяется извне некоторое количество особей такое, что изображающая точка переходит скачком из точки M_1 в точку M_2 . Если после этого систему предоставить самой себе, колебания x(t) и y(t) уже будут возникать с еще большими амплитудами, чем прежде, и изображающая точка будет следовать по траектории 2. Это и значит, что колебания в системе неустойчивы: они навсегда изменяют свои свойства при внешнем воздействии.

2.4. Модели физических процессов (кривая погони, атмосферное давление)

2.4.1.Кривая погони

Пусть задано равномерное движение точки A по некоторой кривой. Необходимо определить траекторию равномерного движения точки P, причем такую, что в любой момент движения можно провести касательную, которая проходила бы через соответствующее этому моменту положение точки A.
Чтобы найти уравнение линии, необходимо выбрать систему координат, в которой ось абсцисс проходит через начальное положение точек P и A, и точка A расположена в начале системы координат xAy. Коэффициент отношения постоянных скоростей точек обозначим через k.
Если предположить, что за бесконечно малый промежуток времени точка A преодолела расстояние dS, а точка A – расстояние dS_1 , то, в соответствии с поставленным выше условием, получим соотношение dS=kdS_1 , или
√(dx^2+dy^2 )=k√(dξ^2+dη^2 ) (23)
Далее следует выразить dξ и dη через x, y и их дифференциалы. По условию, координаты точки P удовлетворяют уравнению касательной к искомой кривой, то есть
η-y=dy/dx(ξ-x)
Добавив к полученному уравнению заданное условием уравнение траектории F(ξ,η) движения «убегающего», могут быть определены из полученной системы уравнения ξ и η. После подстановки этих значений в дифференциальное уравнение (23) оно запишется в виде
Φ(x,y,dy/dx,(d^2 y)/(dx^2 ))=0
Постоянные интегрирования можем найти из начальных условий (y=0,y^’=0 при x=0 ).
В общем случае для произвольно заданной кривой F(ξ,η) получить решение уравнения достаточно сложно. Задача значительно упрощается, если разобрать простейший случай, когда траектория «убегающего» является прямой.
Приведем пример. Пусть миноносец преследует подводную лодку в густом тумане. В некоторый момент времени туман рассеивается и подводная лодка обнаруживается над поверхностью воды на расстоянии 3 миль от миноносца. Скорость миноносца в два раза больше скорости подлодки. Необходимо определить траекторию движения миноносца такую, чтобы он прошел точно над подводной лодкой, если она сразу же после обнаружения погрузилась под воду и ушла на полной скорости прямым курсом в неизвестном направлении.
Чтобы решить данную задачу, необходимо ввести полярные координаты r,θ следующим образом: пусть полюс O находится в точке обнаружения субмарины, а полярная ось r проходит через точку, в которой был миноносец на момент обнаружения подводной лодки (рис.3).

Прежде всего миноносцу необходимо расположиться так, чтобы он и подводная лодка были на одном расстоянии от полюса O. Условие траектории движения миноносца должно быть таким, чтобы оба движущихся объекта всё время были на равном расстоянии от точки O. Тогда миноносец, обходя вокруг полюса O, пройдёт над подводной лодкой. Делаем вывод, что сначала миноносец должен пройти прямым курсом к точке O, пока он не окажется на таком же расстоянии x от полюса O, что и субмарина.
Найдем расстояние x либо из уравнения
x/v=(3-x)/2v
либо из уравнения
x/v=(3+x)/2v
где v – скорость подводной лодки, а 2v – скорость миноносца. Решив последние уравнения, найдем, что либо расстояние x равно одной, либо трём милям.
Если «встреча» не состоялась, то миноносцу необходимо далее продвигаться вокруг полюса O, удаляясь от него со скоростью подводной лодки v. Представим скорость миноносца 2v в виде двух составляющих: радиальной v_r и тангенциальной v_τ (рис. 3).
Радиальная составляющая – это линейная скорость вращения миноносца по отношению к полюсу O, т.е.
v_r=dr/dt
Тангенциальная составляющая – это линейная скорость вращения миноносца по отношению к полюсу. Тангенциальная скорость равна произведению угловой скорости dθ/dt на радиус r, т.е.
v_T=r dθ/dt
Но так как v_r=v, то
v_T=√(〖(2v)〗^2-v^2 )=√3 v
Таким образом, решение исходной задачи можно найти из решения следующей системы двух дифференциальных уравнений
dr/dt=v,r dθ/dt=√3 v,
которая в свою очередь сводится к одному уравнению
dr/r=dθ/√3
исключением переменной t.
Решая полученное дифференциальное уравнение, получаем, что
r=Ce^(θ⁄√3)
где C – произвольная постоянная.
Принимая во внимание движение миноносца вокруг полюса O с полярной оси r на расстоянии x миль от точки O , т.е. учитывая, что r=1 при θ=0 и k=3 при θ=-π, делаем вывод, что в первом случае C=1, а во втором C=3e^(π⁄√3). Таким образом, для выполнения своей задачи, миноносцу необходимо пройти две или шесть миль прямым курсом в направлении места обнаружения подлодки, а затем продолжать движение либо по спирали
r=e^(θ⁄√3),
либо по спирали
r=e^(((θ+π))⁄√3).

2.4.2 Атмосферное давление

Чем выше над уровнем моря, тем воздух разреженнее – атмосферное давление с высотой уменьшается. Определить зависимость p=p(h) давления p от высоты h.
За величину атмосферного давления принимаем вес вертикального столба воздуха с площадью сечения s=1 〖см〗^2. Представим два горизонтальных сечения этого столба воздуха на высотах h и h+∆h. Разность давления на указанных высотах p(h)-p(h+∆h)=-∆p(h) численно представлена весом столбика воздуха между двумя сечениями: -∆p(h)=∆mg, где ∆m – масса этого воздуха, g – ускорение свободного падения. Объем ∆v столбика равен ∆v=s∙∆h=∆h, поэтому если средняя плотность воздуха в столбике равна ρ_ср, то ∆m=ρ_ср ∆h, откуда -∆p(h)=gρ_ср ∆h и ∆p(h)/∆h=-gρ_ср.
Обозначим плотность воздуха на высоте h через p(h). Тогда при ∆h→0 ρ_ср→p(h). Имеем дифференциальное уравнение
dp/dh=-gρ(h) (24)
в котором функция ρ(h) также неизвестна.
Сделаем предположение, что температура воздуха одинакова во всех слоях атмосферы. Тогда
p(h)=bρ(h) (25)
Имеем pV=RT, откуда
p=RT/V=RT/M∙M/V,
где b=RT/M; ρ(h)=M/V;R – универсальная газовая постоянная; M – молярная масса газа.
Из равенств (24) и (25) получаем дифференциальное уравнение
dp/dh=-g/b p (26)
решениями которого являются функции
p=Ce^(-g/b h) (C∈R)
Если над уровнем моря (при h=0) атмосферное давление равно p_0, то C=p_0; закон изменения атмосферного давления в зависимости от высоты над уровнем моря имеет вид
p(h)=p_0 e^(-g/b h) (27)
Итак, давление убывает с высотой по показательному закону в соответствии с полученной так называемой барометрической формулой.[15]

Заключение

В настоящей курсовой работе было рассмотрено математическое моделирование. Создание математических моделей многих физических процессов требует использования дифференциальных уравнений. На сегодняшний день разработано множество методов математического моделирования, в которых используются дифференциальные уравнения. Хотя эти методы обладают тем недостатком, что всегда дают лишь какое-то конкретное решение, что сужает возможности их использования, они, тем не менее, широко используются на практике в процессе познания окружающей нас действительности.
Например, система «хищник-жертва» получила широкое применение в экологии. С помощью этой модели объясняют такие процессы, как колебания численности хищных и мирных животных в промысловых районах, колебания в популяциях рыб, насекомых и т. д.
Впервые перед людьми встала задача построения кривой погони при выборе курса судна, учитывая внешние факторы, такие, как боковые ветра, течения, для оптимального достижения цели путешествия. Затем эта же задача использовалась и в военных целях: достижение и поражение движущихся целей. Также кривая погони нашла применение и в космической навигации.
Главная задача системы самонаведения ракеты – обеспечение попадания её в цель или перехват цели с наименьшим промахом. Так как управляемые ракеты могут менять траекторию своего полёта сразу же после пуска, то существует много траекторий, двигаясь по которым, самонаводящаяся ракета сможет поразить цель. Но на практике выбирают траекторию, обеспечивающую при данных условиях стрельбы наибольшую вероятность поражения цели.
В основу работы системы наведения ракеты положен метод наведения. Он обеспечивает теоретическую траекторию движения ракеты, которая обеспечивается посредством вычислительного устройства с учетом информации об относительном положении ракеты и цели, о скоростях и направлениях их движения. Затем определяется оптимальная траектория движения ракеты и вычисляется наиболее выгодная точка встречи её с целью. По этим вычислениям создаются команды управления, которые поступают на рули управления. Рули управляют ракетой по заданному закону. Одним из методов наведения ракет является использование математических зависимостей, которыми описывается кривая погони.
Барометрический метод измерения высоты полета самолета базируется на зависимости абсолютного давления в атмосфере от высоты. Значение абсолютной высоты необходимо для установления коридоров на маршрутах полета, а также при испытании самолетов, двигателей.
Математическое моделирование имеет огромное значение в нашей жизни: точность полетов обеспечивает нашу безопасность в небе, когда мы путешествуем; при строительстве зданий используется модель прогиба балок и т.д. Можно говорить о многих моделях и процессах и в биологии, и в экологии, и экономике, математическое моделирование проникло во все сферы нашей жизни и приносит огромную пользу.

Список литературы

Агафонов С.А. Дифференциальные уравнения / С.А. Агафонов, А.Д. Герман, Т.В. Муратова. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.-348 с.
Амелькин В.В. Дифференциальные уравнения в приложениях. – М.: Наука. Главная редакция физико-математической литературы, 1987. – 160 с.
Арнольд В.И. Обыкновенные дифференциальные уравнения. — Ижевск 2000.
Боярчук А.К., Головач Г.П. Дифференциальные уравнения в примерах и задачах. — М.: Эдиториал, 2001.
Берестова С.А. Математическое моделирование в инженерии: учебник/С.А. Берестова, Н.Е. Мисюра, Е.А. Митюшов. – Екатеринбург: Изд-во Урал. ун-та, 2018. – 244 с.
Зарубин В.С. Математическое моделирование в технике: Учеб. для вузов/ Под ред. В.С. Зарубина, А.П. Крищенко. – 2-е изд., стереотип. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. – 496 с.
Калинин В.В. Обыкновенные дифференциальные уравнения. — М.: Нефть и газ, 2005.
Кузнецов В.Л. Математическое моделирование: Учебное пособие.- М.: МГТУГА, 2003.
Курант Р. Курс дифференциального и интегрального исчисления. — М.: Наука, 1967.
Осипова Н.В. Математическое моделирование объектов и систем управления: учеб. пособие/Н.В. Осипова. – М.: Изд-во Дом НИТУ «МИСиС», 2019. – 67 с.
Останина А.М. Применение математических методов и ВМ.Мн.:1985
Пискунов Н.С. Дифференциальные и интегральные исчисления / Н.С. Пискунов.- М.: Наука, 2001.Т.2.- 576 с.
Ризниченко Г.Ю. Математическое моделирование биологических процессов. Модели в биофизике и экологии: учеб. пособие для бакалавриата и магистратуры/Г.Ю. Ризниченко. – М.: издательство Юрайт, 2019. – 181 с.
Самаров К.Л. Математика: Учебно-методическое пособие по разделу «Дифференциальные уравнения» — ООО «Резольвента», 2009.
Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения: примеры и задачи. Учеб.пособие. – 2-е изд., перераб. – М.: Высш. шк., 1989. – 383 с.
Тарасик В. П. Математическое моделирование технических систем: Учебник для вузов. — Мн.: ДизайнПРО, 1997. — 640с.
Федорук М.В. Обыкновенные дифференциальные уравнения. — М.: Наука, 1985.
Филиппов А.Ф. Введение в теорию дифференциальных уравнений: Учебник. Изд.2-е, испр. М.:КомКнига, 2007. – 249 с.