Введение
1. Постановка задачи
2. Теория случайных процессов
2.1. Марковские цепи
2.2. Непрерывные Марковские цепи
2.3. Уравнения Колмогорова
3. Теория массового обслуживания
3.1. Система массового обслуживания
3.2. Простейший поток
3.3. Свойства пуассоновского потока
3.4. Механизм обслуживания
3.5. Образование очереди заявок
3.6. Схема СМО
3.7. Граф состояний СМО
4. Описание математической модели
4.1. Вычисление финальных вероятностей
4.2. Конечный результат работы
Список использованной литературы
Введение
Практические требования телефонного дела, физики и рациональной организации массового обслуживания (билетные кассы, магазины, автоматы, рабочие станки и т.п.) выдвинули в начале прошлого столетия ряд интересных математических задач нового типа. Первоначально эти задачи касались преимущественно вопросов обслуживания абонентов телефонной станции, расчета запасов магазинов для бесперебойного снабжения покупателей, а также установления наиболее рационального числа продавцов и касс в торговых предприятиях. На первичное развитие этой теории особое влияние оказали работы известного датского ученого А.К. Эрланга (1879-1929) – многолетнего сотрудника Копенгагенской телефонной компании.
С того времени интерес к проблемам, выдвинутым Эрлангом, необычайно возрос. Оказалось, что задачи типа телефонных возникают в самых разнообразных направлениях исследований: в естествознании, в технике, экономике, транспорте, военном деле, организации производства. Особую роль в постановке задач играют случайные процессы, в особенности процессы Маркова и различные их обобщения.
В тридцатые годы в связи с автоматизацией станков в промышленности наметился переход на обслуживание одним рабочим нескольких станков. Станки в случайные моменты времени в силу тех или иных причин выходят из строя и требуют к себе внимания рабочего. Время приведения станка в рабочее состояние непостоянно, а скорее является случайной величиной. Встают некоторые вопросы: сколько станков будет исправно функционировать, а сколько будет в нерабочем состоянии и будут ожидать ремонта в заданный момент времени? Каково среднее время восстановления одного станка? Можно перечислять дальше, но суть ясна.
Можно указать множество других постановок задач реального содержания, которые в своей математической части сводятся к вопросам теории массового обслуживания.
Однако, математическая теория не может претендовать на перечисление всех частных и даже только важнейших прикладных проблем, к которым она может применяться. Задача математической теории состоит в первую очередь в выработке общих методов, применимых не только к решению тех частных задач, на базе которых была начата ее разработка, но и множество других, быть может, даже очень далеких по своей формулировке от первоначальных.
Постановка задачи
Имеется предприятие, занимающееся производством одноразовой пластиковой посуды. Производство на заводе состоит из N линий, работающих независимо друг от друга и состоящих из оборудования, которое может выйти из строя. Плотность вероятности поломки приборов для всех линий одинакова. Линии, вышедшие из строя, останавливаются и прекращают выпуск продукции до тех пор, пока работоспособность оборудования не будет восстановлена.
Пока оборудование простаивает из-за поломок, предприятие несет несёт убытки в виде упущенной выгоды (линия ничего не производит) и штрафных санкций, в случае, если кампания не успела вовремя выполнить заказ клиента. Для предотвращения полной остановки производства из-за поломок нанимается ремонтная бригада, состоящая из m рабочих, имеющих степень квалификации ϰ. Чем выше количество ремонтников и чем выше их квалификация, тем выше расходы на содержание ремонтной бригады. Чем выше квалификация работника, тем выше стоимость его услуг, но и работу он выполнит быстрее.
Необходимо максимизировать прибыль производства Q=f(m,ϰ) путем минимизации времени простоя работы линий, за счет увеличения расходов на содержание ремонтной бригады. Это предполагает, что мы будем варьировать такими величинами как: количество рабочих m, степень квалификации рабочих ϰ.
Допущения и приближения при постановке задачи
Перед тем, как начать строить математическую модель необходимо ввести допущения для нашей модели: определить, чем можно пренебречь, что можно упростить, ввести какие-либо ограничения и так далее. Список всех допущений представлен ниже:
Персонал на предприятии идеальный: он никогда не опаздывает, не пропускает ни одной смены, таким образом избавляя предприятие от дополнительных рисков;
Входящий поток сырья постоянен и поставляется большими партиями. Также предполагаем, что поставщик сырья надежен и проблемы, связанные с поставками, не возникают;
Время выпуска одной партии значительно меньше времени восстановления работоспособности линии производства, таким образом после восстановления линии, она тут же начнет выпуск новой продукции;
Вероятность выпуска бракованной продукции равна нулю;
Затраты на поставки готовой продукции не рассматриваются;
Вышедшая из строя линия при наличии свободных ремонтников не ждет ремонта, а сразу же начинает восстановление;
Затраты на аренду помещений, потребление электроэнергии не рассматриваются;
Ремонтная бригада в полном составе одновременно занимается ремонтом только одной линии, то есть при наличии более одной поломки часть рабочих не уходит на их восстановление, пока не закончит с первой.
Время восстановления работоспособности линии непостоянно и является случайной величиной, которая распределена по экспоненциальному закону: ()=e^(-), где – интенсивность восстановления.
Поломка оборудования есть Пуассоновский поток событий с интенсивностью поломки .
Оплаты труда рабочих зависит от их квалификации и имеет вид P=f(ϰm),где ϰ степень квалификации и∈[0,1].
Квалификация у всех нанятых специалистов одинаковая.
Теория случайных процессов
Марковские цепи
Рассмотрим физическую систему, которая может находиться в одном из k состояний. В следствии вмешательства случая система шаг за шагом в заданные моменты времени t_1,t_2,…,t_n может скачкообразно менять свое состояние: S_0→S_1→⋯→S_(n-1)→S_n, где 〖{S_k}〗_(k=1)^n – множество возможных состояний системы S. На рис. 1 приведена схема цепи Маркова.
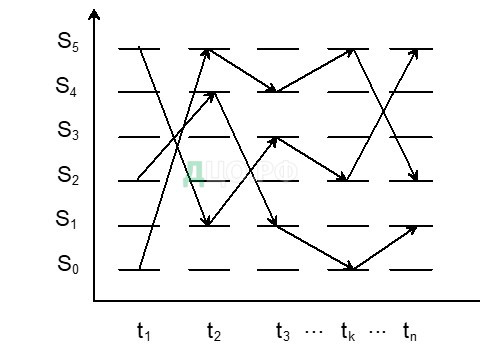
Рисунок 1 Схема цепи Маркова.
Вероятность реализации случайного события s_k^n, состоящего в том, что на n-ом шаге система перейдет в состояние S_k, обозначают как вероятность состояния P_k (n), где на n-ом шаге система находится в k-ом состоянии, то есть P_k (n)=P(s_k^n).
Условную вероятность P(s_k^n |s_p^(n-1)) , дающая вероятность того, что на n¬-ом шаге состояние системы примет значение s_k^n, при условии того, что на предыдущем шаге система была в состоянии s_p^(n-1) принято называть вероятностью перехода (одношагового).
P(s_m^n |s_p^(n+k)) – вероятность перехода за несколько шагов (n-k).
Основная задача для Марковских цепей:
Пусть известно начальное состояние системы и указан вероятностный закон смены состояний (указаны все соответствующие вероятности одношаговых переходов), тогда основная задача заключается в следующем: таким образом можно найти вероятность состояния системы в некоторый момент времени t_n>t_0. В частности при t_n→ ∞.
Для более простой записи вероятности перехода (не одношагового) предлагается использовать следующий формат:
_jk (,n)=P(s_m^n│s_p^(n+k) ); j,k=¯(1,k;) 0≤≤n, (1)
что читается как «вероятность перехода из j-ого состояния на -ом шаге в k-ое состояние на n-ом шаге ».
Так как система на n-ом шаге будет находиться в каком-либо состоянии обязательно, то:
1)∑_(k=1)^k▒〖P_k (n) 〗=1;
2) P_k (n)≥0.
Если система находиться в i-ом состоянии, то она либо останется в этом состоянии, либо перейдет в любое другое, поэтому сумма вероятностей многошагового перехода по всем возможным конечным исходам должна давать единицу:
∑_(k=1)^k▒〖_jk (,n)=1〗; _jk (,n)≥0.
Не трудно убедиться в том, что:
P_k (n)=∑_(j=1)^k▒〖〖P_j ()*〗_jk (,n) 〗, (2)
то есть вероятность на n-ом шаге оказаться в k-ом состоянии есть сумма всех возможных многошаговых переходов из j-ого состояния на -ом шаге в k-ое состояние на n-ом шаге.
Введем квадратную матрицу (n,m)=||_ij (n,m)||.
Вектор вероятностей состояний системы S на n-ом шаге обозначим:
¯P^T (n)=(P_1 (n),P_2 (n),…,P_k (n));
¯P^T (n)=¯P^T () ( ) ̂(,n);
Квадратную матрицу ||a_ij || называют стохастической, если:
∑_(j=1)^k▒a_ij =1; a_ij≥0;
Марковская цепь, для которой матрица вероятности одношаговых переходов не зависит от номера шага, называется однородной. В таком случае матрица двухшагового перехода будет ( ) ̂^2, для n-шагового перехода будет ( ) ̂^n.
Однородная цепь Маркова для которой вероятность P_k (n) не зависит от n называется стационарной.
Если для цепи Маркова с конечным числом состояний выполняется условие _ij (n,m)>0 (отсутствуют запрещенные переходы), то существуют предельные вероятности P_k, то есть вероятность обнаружить систему в состоянии k в заданный момент времени, причем P_k не зависит от P_k (0).
P_k в этом случае находится из системы уравнения:
{█(P_k=∑_(j=1)^k▒〖P_j _jk;〗@∑_(k=1)^k▒P_k =1.)┤ (3)
Однородную цепь Маркова удобно представить в виде графа, вершины которого возможные состояния, а дуги – переходные вероятности (рис. 2).
Рисунок 2 Граф однородной цепи Маркова
Непрерывные Марковские цепи
Процессы в системах с дискретными состояниями и непрерывным временем называются непрерывными Марковскими цепями. Рассмотрим Марковский процесс с дискретными состояниями, описывающий поведение системы S с множеством возможных состояний 〖{S_k}〗_(k=1)^n. Событие s_k^t обозначает, что в момент времени t∈T система S находится в состоянии k, тогда получаем:
p_k (t)≡P[s_k^t ],t∈T .
В этом случае вектор вероятностей состояний
¯P^T (t)=(P_1 (t),P_2 (t),…,P_k (t));
Определяет вероятности состояний системы S в момент времени t∈T.
Пусть S – некоторая система с возможными состояниями 〖{S_k}〗_(k=1)^n. Под плотностью вероятности перехода этой системы из состояния S_i в состояние S_j в момент времени t понимают число
_ij (t)≡lim┬(∆t→0)〖(P_ij (t,∆t))/∆t〗,
Где P_ij (t,∆t) – вероятность того, что система S, находившаяся в момент времени t в состоянии S_i, за время ∆t>0 перейдет в состояние S_j.
Скалярный Марковский процесс с дискретными состояниями называется однородным, если для любых i,j _ij (t) не зависит от времени, то есть является константой:
_ij (t)=const,t∈T.
В противном случае процесс называется неоднородным.
Если для всех пар состояний S_i и S_j из множества возможных состояний системы S известны плотности вероятностей перехода {_ij (t)}, то граф состояний системы S можно превратить в размеченный граф состояний, проставив у стрелок не переходные вероятности, а плотности вероятностей перехода (рис. 3).
Рисунок 3 Размеченный граф состояний
Уравнения Колмогорова
Пусть система S имеет множество возможных состояний 〖{S_k}〗_(k=1)^n, а процесс изменения состояний этой системы представляет собой случайный процесс, причем для все пар возможных состояний S_i и S_j определены плотности вероятностей переходов _ij (t) и _ji (t). Тогда вероятности состояний системы p_k (t) удовлетворяют системе уравнений Колмогорова:
〖p^’〗_k (t)=∑_█(i=1@i≠k)^n▒〖_ik (t) p_i (t) 〗-∑_█(i=1@i≠k)^n▒〖_ki (t) p_k (t) 〗,k=¯(1,n),t∈T. (4)
Получается, что 〖p^’〗_k (t) есть сумма входящих и выходящих потоков. Входящие потоки ∑_█(i=1@i≠k)^n▒〖_ik (t) p_i (t) 〗берутся со знаком плюс, а выходящие ∑_█(i=1@i≠k)^n▒〖_ki (t) p_k (t) 〗 со знаком минус.
Теория массового обслуживания
Система массового обслуживания
Система массового обслуживания (СМО) состоит из следующих элементов:
Входящий поток заявок, требований;
Приборы, обслуживающие заявки;
Очередь заявок.
Простейший поток
В большинстве задач по теории массового обслуживания рассматривается простейший случай потоков, когда вероятность поступления в промежуток времени t ровно k требований задается формулой:
P_k (t)=(t)^k/k! e^(-t), (5)
где k – случайная величина, распределённая по пуассоновскому закону, а данный поток называется пуассоновским. >0- постоянное число, поток заявок: =1/¯t, где ¯t среднее время между поступлением заявок. Поток заявок является дискретным и одновременно не может поступить более одной заявки.
Свойства пуассоновского потока
Поток называется стационарным пуассоновским или простейшим потоком, если он обладает следующими свойствами: стационарностью, отсутствием последействия, ординарностью.
Стационарность потока означает, что для любых групп, состоящих из счетного числа непересекающихся отрезков времени, k1, k2, …, kn, будут зависеть только от ,t и длин указанных промежутков времени, но не будут зависеть от их расположения на оси времени. То есть, вероятность появления k требований P_k (t) в промежутке времени (T;T+) не зависит от T.
Отсутствие последействия состоит в том, что для любых непересекающихся участков времени, вероятность попадания на один из них не влияет на вероятность попадания на другой участок. Иными словами, будущее не зависит от прошлого, а прошлое не зависит от будущего.
Ординарность потока требований пресекает возможность появления более одной заявки за один момент времени.
Механизм обслуживания
По числу каналов обслуживания СМО делятся на две группы:
Одноканальные – когда в системе ровно один обслуживающий прибор;
Многоканальные – когда в системе имеется более одного обслуживающего прибора.
В зависимости от взаимного расположения каналов СМО делятся также на два типа:
Параллельное расположением приборов – когда обслуживание заявок происходит параллельно и не зависит друг от друга;
Последовательное расположение приборов – в таком случае заявка проходит последовательную обработку всех приборов, находящихся в данной СМО.
Обслуживающие приборы характеризуются интенсивностью обслуживания и принципом обслуживания. Интенсивность обслуживания определяется как =1/¯t_обс , где ¯t_обс – среднее время обслуживания заявки прибором. Выделяются следующие принципы обработки заявок:
На одно требование – один прибор;
Если свободно несколько приборов, то они параллельно могут обслуживать одну заявку – это групповое обслуживание;
Многофазовое обслуживание – когда заявка проходит поэтапное обслуживание несколькими приборами.
Время обслуживания прибора не постоянная величина, а случайная и подчиняется какому-то закону распределения, какому именно – это зависит от условия поставленной задачи.
Образование очереди заявок
В зависимости от возможности образования очереди СМО делятся на три группы:
Системы с отказами в обслуживании – в таких системах образование очереди невозможно, все заявки, поступившие в момент времени, когда все приборы заняты, получают отказ и теряются;
Системы с ограничением на длину очереди – в таких системах очередь имеет ограниченное число возможных заявок.
Системы без ограничений – в таких системах длина очереди бесконечно, таким образом количество заявок, которые могут находится в очереди, может расти до бесконечности.
По дисциплине очереди СМО делятся на две группы:
Обслуживание в порядке очереди – обработка запроса в таком случае руководствуется простым принципом: «первым пришел – первым ушел».
Обслуживание по приоритету – заявки, имеющие высокий приоритет, будут обработаны раньше остальных, не обращая внимание на то, каким по счету они прибыли в систему;
Схема СМО
Таким образом, основные элементы системы массового обслуживания укладываются в следующую схему (рис. 4):
Рисунок 4 Схема СМО
Граф состояний СМО
При анализе случайных процессов удобно пользоваться вариантом схематического изображения возможных состояний систем массового обслуживания на рисунке в виде графа с разметкой его возможных состояний (рис. 5).
Рисунок 5 Граф состояний СМО
Система может находиться в одном из Sn состояний.
Описание математической модели
Рассмотрим прибыль предприятия Q, которая зависит от множества факторов, в том числе и от простоев линий производства, которые ломаются с интенсивностью – чем больше простоев, тем меньше прибыль. На восстановление оборудования кампания выделяет средства на содержание ремонтной бригады, занимающейся восстановлением линий. Интенсивность восстановления ϰ^’µ,где ϰ^’=mϰ, зависит от квалификации рабочих ϰ и от количества рабочих в ремонтной бригаде m.
Рассмотрим R- среднее число произведенной продукции, которая зависит от простоев линии, R=R(ϰ^’ ):
R(ϰ^’ )=∑_(k=0)^N▒〖P_(n-k) (ϰ^’)k〗 V, (6)
где P_(n-k) (ϰ^’)– предельная вероятность обнаружить систему в (n-k)-ом состоянии в любой момент времени после перехода системы в стационарный режим. V- объем выпускаемой продукции на одной линии за период времени T, k – количество рабочих линий. Тенденция такова: при k=0, когда все линии простаивают, ничего не производится; при k=1, когда работает только одна линия, а все остальные простаивают из-за поломок, производство идет только на одной линии, соответственно в таком случае будет выпущено kV=1*V=V товаров, но за период времени T не всегда будет так, что будет работать только одна линия, есть лишь некая предельная вероятность P_(n-k) обнаружить систему в состоянии G_(n-k), когда в рабочем состоянии находится только одна линия, поэтому kV умножаем на предельную вероятность P_(n-k) (ϰ^’). Тоже самое и для остальных k.
Рассмотрим E(ϰ^’ )- затраты на содержание ремонтной бригады, которые зависят от количества ремонтников и их квалификации. Эта зависимость в разных ситуациях может сильно различаться. Например, если скорость роста заработной платы увеличивается при увеличении степени квалификации, как на графике (рис. 6):
Рисунок 6 График зависимости скорости роста заработной платы от степени квалификации
то наем специалистов с высокой квалификацией будет намного дороже, чем наем менее квалифицированных рабочих. Поэтому в таком случае лучше нанять низко или средне квалифицированных рабочих, но в большем количестве, чем нанять рабочих высокой квалификации, но меньше. Это при условии, что плотность восстановления ϰ’ будет одинакова в обоих вариантах. Затраты на содержание ремонтной бригады в первом варианте выглядят так:
E(ϰ^’ )=mE(ϰ),(7)
таким образом количество рабочих m выносится за скобку.
В другом случае, если скорость роста заработной платы уменьшается при увеличении степени квалификации, как показано на графике (рис. 7):
Рисунок 7 Скорость роста заработной платы уменьшается при увеличении степени квалификации
то ситуация ровно наоборот: лучше нанять одного очень хорошего специалиста, чем несколько, не имеющих хорошей подготовки. Тогда затраты на содержание ремонтной бригады будут рассчитываться следующим образом:
E(ϰ^’ )=E(mϰ). (8)
Для более наглядно примера описания математической модели было решено остановиться на следующей зависимости:
E(ϰ^’ )=ϰ^’ e^(ϰ^’ ). (9)
В конечном итоге прибыль производства Q(ϰ^’ ) примет следующий вид:
Q=qVR(ϰ^’ )-E(ϰ^’ ); (10)
Q=q∑_(k=0)^N▒〖P_(n-k) (ϰ^’)k〗-ϰ^’ e^(ϰ^’ ); (11)
q- цена продажи одной партии.
4.1. Вычисление финальных вероятностей
Представим наш процесс в виде графической схемы (рис. 8):
Рисунок 8 Графическая схема
Так как время восстановления работоспособности линии непостоянно и является случайной величиной, которая распределена по экспоненциальному закону: ()=e^ϰ’, где – интенсивность восстановления, ϰ^’=mϰ, m – число рабочих, ϰ – степень квалификации рабочих, ϰ ϵ [0,1], то плотность перехода из состояния G_k в G_(k-1) будет ϰ’, k=¯(1,n).
Дифференциальные уравнения Колмогорова (12):
{█((P_0 ) ̇(t)=ϰ’P_1-nP_0;@(P_1 ) ̇(t)=nP_0+ϰ’P_2-((n-1)+ϰ’) P_1;@(P_2 ) ̇(t)=(n-1)P_1+ϰ’P_3-((n-2)+ϰ’) P_2;@…@(P_i ) ̇(t)=(n-i+1)P_(i-1)+ϰ’P_(i+1)-((n-i)+ϰ’) P_i;@…@(P_n ) ̇(t)=P_(n-1)-ϰ’P_n.) (12)┤
Рассмотрим стационарный случай, то есть когда вероятность обнаружить систему в i-ом состоянии не меняется:
(dP_i)/dt=0,i=¯(0,n);
Получаем систему уравнений (13):
{█(█(0=ϰ^’ P_1-nP_0;@0=nP_0+ϰ^’ P_2-((n-1)+ϰ^’ ) P_1;@0=(n-1)P_1+ϰ^’ P_3-((n-2)+ϰ^’ ) P_2;@…@0=(n-i+1)P_(i-1)+ϰ^’ P_(i+1)-((n-i)+ϰ^’ ) P_i;@…@0=P_(n-1)-ϰ^’ P_n.) (13) @ )┤
Решаем её:
{█(█(nP_0=ϰ^’ P_1;@((n-1)+ϰ^’ ) P_1=nP_0+ϰ^’ P_2;@((n-2)+ϰ^’ ) P_2=(n-1)P_1+ϰ^’ P_3;@…@((n-i)+ϰ^’ ) P_i=(n-i+1)P_(i-1)+ϰ^’ P_(i+1);@…@ϰ^’ P_n=P_(n-1).) (14) @ )┤
Находим:
nP_0=ϰ^’ P_1
(n-1)P_1+ϰ^’ P_1=ϰ^’ P_1+ϰ^’ P_2=> (n-1)P_1=ϰ^’ P_2;
(n-2)P_2+ϰ^’ P_2=(n-1)P_1+ϰ^’ P_3=> (n-2)P_2=ϰ^’ P_3;
(n-i)P_i+ϰ^’ P_i=(n-i+1)P_(i-1)+ϰ^’ P_(i+1)=>(n-i)P_i=ϰ^’ P_(i+1);
ϰ^’ P_n=P_(n-1).
Отсюда нетрудно заметить, что в стационарном режиме вероятности обнаружения системы в любых двух соседних допустимых состояниях связаны простыми соотношениями (15):
{█(P_0=(ϰ^’ )/n P_1;@P_1=(ϰ^’ )/((n-1)) P_2;@P_2=(ϰ^’ )/((n-2)) P_3;@P_i=(ϰ^’ )/(n-i) P_(i+1);@P_n=(ϰ^’ )/ P_(n-1);)┤ (15)
Перемножив предыдущие равенства (15), получим:
P_0=(ϰ^’ *ϰ^’ *ϰ^’ *…*ϰ^’ )/(n*(n-1)*(n-2)*…*(n-i)) P_i,i≥3;
P_i=(n!/(n-i)! )/(ϰ^’ 〖^〗) P_0,i≥3;
Суммируя по i и учитывая, что ∑_(i=0)^(N-1)▒〖P_i=1〗, находим:
Рисунок 9 Графики состояний
На рис. 9 изображены графики состояния СМО в заданный момент времени. Рисунок не является результатом какой-то работы, он лишь демонстрирует то, как система переходит в стационарный режим. График P0 исходит из единицы, так как в начальный момент времени все каналы СМО свободны, соответственно именно поэтому графики остальных состояний каналов исходят из нуля. В какой-то момент графики состояний переходят в стационарный режим, когда вероятность нахождения системы в состоянии k больше не меняется – это и есть предельная вероятность.
Чтобы решить систему дифференциальных уравнений Колмогорова (1), нужно прировнять левую часть системы уравнений нулю и решить систему относительно P_1,P_2,…,P_n. Однако при большом количестве уравнений разрешить такую систему вручную будет тяжело, даже используя метод простых итераций или метод Гаусса. Поэтому необходимо воспользоваться дополнительным программным обеспечением.
Это не единственный метод: можно провести численное интегрирование дифференциальных уравнений с помощью метода Эйлера.
4.2. Конечный результат работы
В конечном результате получаем функцию, которая описывает зависимость прибыли предприятия от состава ремонтной бригады: от количества ремонтников и их квалификации:
Q=qV∑_(k=1)^N▒〖P_k (N-K)〗-E(ϰ^’ );
P_k – предельная вероятность обнаружить систему в k-ом состоянии;
q- цена продажи одной партии;
V- объем выпускаемой продукции на одной линии за период времени.
Полученная модель имеет ряд приближений и допущений: что-то мы упростили, что-то не учитывали вовсе. При дальнейшей разработке и развитии данной модели можно отказаться от некоторых приближений, чтобы получить более полную картину происходящего.
Математическая модель есть отображение реальности, которая позволяет изучить процессы, протекающие в этой реальности. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования.
Список использованной литературы
Вентцель Е.С. Исследование операций : задачи, принципы, методология : учеб. пособие / Е.С. Вентцель.— 5-е изд., стер. — М. : Высш. шк., 2010 .— 191 с.
Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. — М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. — 448 с.
Гнеденко Б. В., Коваленко И.Н., Введение в теорию массового обслуживания. Издательство «Наука», главная редакция физико-математической литературы. Москва 1966.
Солодовников А.С. Математика в экономике : учебник для вузов. Ч.1 / А.С. Солодовников [и др.] .— 2-е изд., перераб. и доп. — М. : Финансы и статистика, 2007 .— 384с.
Экономико-математические методы и модели : учеб. пособие / В.М. Тихобаев [и др.] ; ТулГУ. – Тула: Изд-во ТулГУ, 2007. – 151 с.
Васин А.А. Исследование операций : учеб. пособие для вузов / А.А. Васин, П.С. Краснощеков, В. В. Морозов.— М. : Академия, 2008.— 464 с.
Горбунова Р.И. Экономико-математические методы и модели : учеб. пособие / Р.И. Горбунова [и др.]; под ред. С.И. Макарова.— М. : КНОРУС, 2007.— 232с.
Исследование операций в экономике : учеб. пособие для вузов / Н.Ш. Кремер [и др.] ; под ред. Н. Ш. Кремера.— 2-е изд., перераб. и доп.— М. : Юрайт, 2010.— 431 с.
Административно-управленческий портал www.aup.ru
Портал Статосфера http://statosphere.ru
