ВВЕДЕНИЕ
Глава 1. Теоретические основы теории игр и модели линейного программирования
1.1. Линейные модели. Задачи линейного программирования
1.2. Основы теории игр
1.3. Метод линейного программирования в теории игр
Глава 2. Построение экономико-математических задач линейного программирования как частного случая теории игр
2.1. Графический метод решения задачи линейного программирования
2.1.1 Методика решения задач ЛП графическим методом.
2.2. Применение графического метода решения задачи линейного программирования на практике
2.2.1. Нахождение оптимального решения задачи с помощью линейного метода.
2.3. Анализ чувствительности оптимального решения задач линейного программирования
2.3.1. Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)
2.3.3. Третья задача анализа на чувствительность (в каких пределах допустимо изменение коэффициентов целевой функции)
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Основой для решения экономических задач являются математические модели. Линейное программирование — один из важнейших разделов ма-тематики, изучающий теории и методы решения определенных задач. Эта математическая дисциплина стала в последние годы широко применяться в различных областях экономики, техники и военного дела, где в их разви-тии не последнюю роль играет математическое планирование и использо-вание компьютеров. Данный раздел науки изучает линейные оптимизаци-онные модели.
Иначе говоря, линейное программирование посвящено численному анализу и решению задач, требующих нахождения оптимального значе-ния, т.е. максимума или минимума, некоторой системы показателей в про-цессе, а состояние его описывает система линейных неравенств. [10]
Впервые термин «линейное программирование» предложил амери-канский экономист Купманс Т. в 1951 году. В 1975 году русский матема-тик Канторович Л.В. и Купманс Т. были удостоены Нобелевской премии по экономическим наукам за свой вклад в теорию оптимального распреде-ления ресурсов. Купманс Т. пропагандировал методы линейного про-граммирования и защищал приоритеты Канторовича Л.В., открывшего эти методы. Канторович Л.В. изучал возможность применения математики к вопросам планирования, на основе чего в 1939 году была опубликована его монография «Математические методы организации и планирования производства».
Важнейшей находкой Канторовича Л.В. явилась возможность четко математически сформулировать важнейшие производственные задачи, что позволяет найти количественный подход к данным задачам, а также их решение численными методами. Если бы его первые работы получили в свое время должную оценку, то была бы велика вероятность еще большего продвижения линейного программирования в настоящее время.
К сожалению, его работа оставалась в тени как в Советском Союзе, так и за его пределами, и, как отмечает Данциг: » …и за это время линейное программирование стало настоящим искусством». Начало широкого ис-пользования линейных зависимостей для описания экономических явле-ний, многие из которых вовсе не обладают свойством линейности, было в середине ХХ в. подлинной научной революцией. Ее даже так и называли — “линейная революция в экономике”. Она дала мощный толчок развитию экономико-математических методов, способствовала всестороннему фор-мированию практически применимого математического аппарата для ис-следования разнообразных областей экономики.
Но необходимо учитывать, что многие экономические процессы в действительности носят нелинейный и стохастический характер и их ап-проксимация линейными зависимостями (линеаризация), упрощая расче-ты, существенно огрубляет и искажает их. Поэтому линейные модели страдают известной ограниченностью в том, что касается отображения с их помощью реальных экономических процессов. [8]
Но во многих случаях созданный на этой основе математический ап-парат в сочетании с компьютерной техникой, производящей сложные и трудоемкие расчеты, позволяет с успехом использовать такие модели в хо-зяйственной практике и в экономической науке.
Так, на сегодняшний день, линейное программирование объединяет в себе методы оптимизации моделей, в которых целевые функции строго ли-нейны, а область допустимых решений – выпуклый многогранник. Благо-даря своей простоте и компьютерной эффективности алгоритмы линейного программирования нашли свое применение как самостоятельно, так и в со-ставе более сложных типов моделей и задач.
Целью курсовой работы является систематизация теоретических зна-ний и практических навыков в области применения математических мето-дов и моделей исследования операций в экономике.
Актуальность темы исследования обусловлена тем, что если при изу-чении задач линейного программирования основное внимание уделяется способу эффективного использования ограниченных ресурсов, то в теории игр основное внимание уделяется стратегиям, при помощи которых дости-гаются интересующие нас цели. Однако между задачами теории игр и ли-нейного программирования существует связь, позволяющая применять из-вестные нам методы.
Объект исследования – модели линейного программирования.
Предмет исследования – рассмотрение модели линейного програм-мирования как частного случая теории игр.
В рамках выполнения работы предстоит решить ряд следующих за-дач:
1. Изучить теоретические основы модели линейного программи-рования и их задачи.
2. Изучить теоретические основы теории игр.
3. Изучить модели линейного программирования как частный случай теории игр.
4. Построить экономико-математическую задачу линейного про-граммирования.
5. Найти оптимальное решение задачи линейного программиро-вания на практике.
6. Провести анализ чувствительности оптимального решения за-дачи Данная курсовая работа состоит из введения, двух глав, заключения и списка использованной литературы.
Для написания курсовой работы использовались работы наикруп-нейших мыслителей, учебная и справочная литература, и также итоги фак-тических изучений представительных российских и иностранных писате-лей.
Основными авторы, в научных произведениях которых рассматри-валась проблема исследования являются Алексеева Е.В., Колодникова Н.Б, Вентцель Е.С., Конюховский П.В. и другие.
Глава 1. Теоретические основы теории игр и модели линейного программирования
1.1. Линейные модели. Задачи линейного программирования
Математической моделью задачи называется совокупность матема-тических соотношений, описывающих суть задачи.
Линейное программирование — это область математического про-граммирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными.
Составление математической модели включает:
— выбор переменных задачи;
— составление системы ограничений;
— выбор целевой функции.
Переменными задачи называются величины Х1, Х2, Хn, которые полностью характеризуют экономический процесс. Обычно их записывают в виде вектора: X= (X1, X2,…,Xn).
Системой ограничений задачи называют совокупность уравнений и неравенств, описывающих ограниченность ресурсов в рассматриваемой задаче.
Целевой функцией задачи называют функцию переменных задачи, которая характеризует качество выполнения задачи, экстремум которой требуется найти.
Слово “программирование” объясняется здесь тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно в совокупности определяют программу работы некоторого экономического объекта. Слово “линейное” отражает факт линейной зависимости между переменными. При этом задача обязательно имеет экстремальный харак-тер, т. е. состоит в отыскании экстремума (максимума или минимума) целе-вой функции. [11]
Основная задача линейного программирования (ОЗЛП) ставится следующим образом: Имеется ряд переменных . Требуется найти такие их неотрицательные значения, которые удовлетворяли бы системе линейных уравнений:
{1.1}
и, кроме того, обращали бы в минимум линейную целевую функцию (ЦФ)
Очевидно, случай, когда ЦФ нужно обратить не в минимум, а в мак-симум, легко сводится к предыдущему, если изменить знак функции и рас-смотреть вместо нее функцию
Допустимым решением ОЗЛП называют любую совокупность пере-менных , удовлетворяющую уравнениям (1.1).
Оптимальным решением называют то из допустимых решений, при котором ЦФ обращается в минимум.
На практике ограничения в задаче линейного программирования ча-сто заданы не уравнениями, а неравенствами. В этом случае можно перей-ти к основной задаче линейного программирования.
Рассмотрим задачу линейного программирования с ограничениями-неравенствами, которые имеют вид
{1.2}
и являются линейно-независимыми. Последнее означает, никакое из них нельзя представить в виде линейной комбинации других. Требуется найти , которые удовлетворяют неравенствам и обращают в минимум
Введём уравнения:
{1.3}
где — добавочные переменные, которые также как и явля-ются неотрицательными.
Таким образом, имеем общую задачу линейного программирования — найти неотрицательные , чтобы они удовлетворяли системе уравнений (1.3) и обращали в минимум .
Коэффициенты в формуле (1.3) перед равны нулю.
Так, линейное программирование – метод решения задач оптимиза-ции.
В первых оптимизационных задачах требовалось выяснить, сколько различных изделий нужно произвести, чтобы получить максимальный до-ход, если известно количество ресурсов (сырья, рабочего времени, обору-дования) и цены, по которым можно реализовать готовые изделия. Другой вид задач – выяснить, при каких условиях свести расходы к минимуму.
Таким образом, общая задача линейного программирования – это задача, в которой требуется найти максимум или минимум (оптимум) функции, называемой функцией цели, при ограничениях, заданных систе-мой линейных неравенств или уравнений. [1]
При этом переменные чаще всего по условиям задачи должны при-нимать неотрицательные значения, то есть положительные либо нулевые, но бывают и исключения. И система ограничений, и целевая функция име-ют линейный характер, то есть содержат переменные только в первой сте-пени.
Канонической задачей линейного программирования называется за-дача, в которой, как было показано выше, требуется найти максимум целе-вой функции при ограничениях, заданных системой линейных уравнений.
Задачей линейного программирования в стандартной, или, как гово-рят иначе, нормальной форме, называется задача, в которой требуется найти максимум целевой функции при ограничениях, заданных системой неравенств одного смысла, то есть с одинаковым знаком, и этот знак — «меньше или равно», причём действует также условие неотрицательности переменных.
Если в задаче линейного программирования, заданной в стандарт-ной форме, требуется найти минимум целевой функции, то система огра-ничений состоит из системы неравенств со знаком «больше или равно».
Задачей линейного программирования в общей форме, или, как го-ворят иначе, в смешанной форме, называется задача, в которой требуется найти максимум или минимум целевой функции, а система ограничений может включать в себя неравенства с различными знаками, а также урав-нения, то есть равенства.
При этом в задаче, заданной в общей форме, условие неотрицатель-ности переменных не обязательно соблюдается, то есть некоторые пере-менные могут быть без ограничения знака, а для некоторых, как, впрочем, иногда и всех, переменных может быть задано условие неположительно-сти. [8]
Если все или некоторые ограничения в системе заданы неравенства-ми, то задачу можно свести к канонической путём преобразования нера-венств в уравнения.
Множество чисел, запись последовательности иксов, удовлетворяю-щих системе ограничений, называется решением этой системы. Решение системы также часто называется планом, и немного реже – программой, но именно отсюда и пошло название «линейное программирование».
Оптимальным решением задачи линейного программирования назы-вается решение системы, при которых функция цели обращается в макси-мум или минимум, в зависимости от условия задачи, или в общем смысле – в оптимум.
Решение задачи линейного программирования называется вырож-денным, если в нём некоторые переменные равны нулю. В противном слу-чае решение является невырожденным.
Как было отмечено выше, переменные в задаче линейного програм-мирования чаще всего должны быть неотрицательными, но, как мы уже усвоили, общая форма записи задачи допускает и отрицательные значения переменных. Если переменные, икс с индексом, означают наличность фир-мы, которую требуется направить на различные нужды, но по некоторым статьям фирма должна денег больше, чем имеет, то тогда можно допу-стить, что соответствующие переменные – отрицательные.
К приведённым определениям следует добавить следующее правило, имеющее практическое значение. Для того чтобы решение задачи имело смысл, ограничения задачи линейного программирования должны быть заданы в одних и тех же единицах. [4]
Например, если фигурантами задачи линейного программирования являются трудодни, то необходимо определить, идёт ли речь о трудоднях в неделю или в месяц и определённого уточнения придерживаться на всём протяжении решения задачи.
Задачи линейного программирования в случае двух переменных можно решить и графическим методом, в случаях, когда переменных больше, применяется симплекс-метод.
Теперь перейдем к рассмотрению вопроса основ теории игр, и сфор-мулируем выводы первой главы о моделях линейного программирования как частного случая теории игр.
1.2. Основы теории игр
На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в условиях неопределенности, т.е. возни-кают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от меро-приятий партнера. Такие ситуации, возникающие при игре в шахматы, шашки, домино и т.д., относятся к конфликтным: результат каждого хода игрока зависит от ответного хода противника, цель игры —выигрыш од-ного из партнеров.
В экономике к конфликтным ситуациям относятся, например, взаи-моотношения между поставщиком и потребителем, покупателем и продав-цом, банком и клиентом. Во всех этих примерах конфликтная ситуация порождается различием интересов партнеров и стремлением каждого из них принимать оптимальные решения, которые реализуют поставленные цели в наибольшей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнера, и учитывать неизвест-ные заранее решения, которые эти партнеры будут принимать. [6]
Для грамотного решения задач с конфликтными ситуациями необхо-димы научно обоснованные методы. Такие методы разработаны матема-тической теорией конфликтных ситуаций, которая носит название теория игр.
Математическая модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте, —игроками, а исход конфликта — выигрышем. Для каждой формализованной игры вводятся правила, т.е. система условий, определяющая:
— варианты действий игроков;
— объем информации каждого игрока о поведении партнеров;
— выигрыш, к которому приводит каждая совокупность действий.
Как правило, выигрыш (или проигрыш) может быть задан количе-ственно; например, можно оценить проигрыш нулем, выигрыш —единицей, а ничью — 1/2.
Игра называется парной, если в ней участвуют два игрока, и множе-ственной, если число игроков больше двух. Мы будем рассматривать только парные игры. В них участвуют два игрока А и В, интересы кото-рых противоположны, а под игрой будем понимать ряд действий со сто-роны А и В.
Игра называется игрой с нулевой суммой, или антагонистической, если выигрыш одного из игроков равен проигрышу другого, т.е. для пол-ного задания игры достаточно указать величину одного из них. Если обо-значить а —выигрыш одного из игроков, b — выигрыш другого, то для игры с нулевой суммой b = —а, поэтому достаточно рассматривать, например а.
Выбор и осуществление одного из предусмотренных правилами дей-ствий называется ходом игрока. Ходы могут быть личными и случайными. Личный ход —это сознательный выбор игроком одного из возможных действий (например, ход в шахматной игре). Случайный ход —это слу-чайно выбранное действие (например, выбор карты из перетасованной ко-лоды). В дальнейшем мы будем рассматривать только личные ходы игро-ков. [9]
Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложив-шейся ситуации. Обычно в процессе игры при каждом личном ходе игрок делает выбор в зависимости от конкретной ситуации.
Однако в принципе возможно, что все решения приняты игроком за-ранее, в ответ на любую сложившуюся ситуацию. Это означает, что игрок выбрал определенную стратегию, которая может быть задана в виде спис-ка правил или программы. Так можно осуществить игру с помощью ЭВМ. Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной —в противном случае.
Для того чтобы решить игру, или найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оп-тимальности, т.е. один из игроков должен получать максимальный выиг-рыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый придерживает-ся своей стратегии. Такие стратегии называются оптимальными. Опти-мальные стратегии должны также удовлетворять условию устойчивости, т.е. любому из игроков должно быть невыгодно отказаться от своей стра-тегии в этой игре.
Если игра повторяется достаточно много раз, то игроков может ин-тересовать не выигрыш и проигрыш в каждой конкретной партии, а сред-ний выигрыш (проигрыш) во всех партиях.
Целью теории игр является определение оптимальной стратегии для каждого игрока. При выборе оптимальной стратегии естественно предпо-лагать, что оба игрока ведут себя разумно с точки зрения своих интересов.
Важнейшее ограничение теории игр — единственность выигрыша как показателя эффективности, в то время как в большинстве реальных экономических задач имеется более одного показателя эффективности.
Более общим понятием, чем чистые (максиминные, минимаксные) стратегии в теории игр являются смешанные стратегии, использующие ве-роятностные распределения. Такой подход позволяет строить более гибкие стратегии и разрешать ситуации с возникшей неустойчивостью в чистых стратегиях. Решение матричной игры возможно осуществить аналитиче-ским и графическим методом. [7]
Но в случае большого количество стратегий у игроков и отсутствия седловой точки и цены игры в чистых стратегиях, к сожалению, аналити-ческий и графический методы не применимы. В таких ситуациях оправды-вает себя применение теории линейного программирования.
Рассмотрим более подробно решение матричной игры сведением ее к задаче линейного программирования.
1.3. Метод линейного программирования в теории игр
Пусть имеем игру размерности m×n с матрицей (1.4):
{1.4}
Обозначим через Р* = (р1*, р2*, …,рm*), Q* = (q1*, q2*,…,qn*) оп-тимальные смешанные стратегии игроков А и В.
Применение оптимальной стратегии Р* = (р1*,р2*,…,рm*) гаранти-рует игроку А выигрыш, не меньший ν, независимо от выбора стратегии Bj игроком В. Математически это запишется в виде (1.5):
{1.5}
где
Аналогично, стратегия Q* = (q1*, q2*,…, qn*) гарантирует игроку В проигрыш, не больший ν, независимо от выбора игроком А стратегии Аi, т. е.
{1.6}
Где
Таким образом, мы получили пару двойственных симметричных за-дач линейного программирования.
Поскольку элементы платежной матрицы всегда можно сделать по-ложительными, то можно считать, что и цена игры ν > 0. Упростим систе-мы (1.5.) и (1.6.), разделив обе части каждого неравенства систем на ν и введя новые обозначения (рис. 1.7). [9]
Решая задачу для игрока А, определяем оптимальный вектор Х* = (х1*;х2*;…;хm*) и f* = fmin, а затем
В результате решения задачи для игрока B получаем оптимальный вектор У* = (у1*;у2*;…;уn*) и ϕ* = ϕmax, а затем
{1.7}
Замечание 1. Поскольку записанные задачи образуют пару двой-ственных задач линейного программирования, то нет необходимости ре-шать обе задачи. Получив оптимальное решение одной из задач, далее до-статочно из последней симплексной таблицы выписать решение двойствен-ной задачи, при этом используется соответствие свободных и базисных пе-ременных прямой и двойственной задач и оценок f-строки (1.8):
{1.8}
Замечание 2. Если решение одной из задач удалось найти графиче-ским методом, то далее для получения оптимального решения двойствен-ной задачи следует воспользоваться условиями дополняющей нежесткости. Из этих условий следует, что если какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом обращается в строгое равен-ство. Если какое-либо неравенство системы ограничений одной из задач своим оптимальным планом обращается в строгое неравенство, то соответ-ствующая компонента оптимального плана двойственной задачи равна ну-лю. [7]
Так, в данной главе настоящей курсовой работы мы рассмотрели теоретические понятия основы теории игр, а также изучили модели линей-ного программирования. Рассмотрели связь линейного программирования и решения матричных игр. Перейдем к вопросу построения экономика-математической задачи линейного программирования.
Глава 2. Построение экономико-математических задач линейно-го программирования как частного случая теории игр
2.1. Графический метод решения задачи линейного программирова-ния
Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на гео-метрическом представлении допустимых решений и ЦФ задачи.
Каждое из неравенств задачи линейного программирования (1.2) определяет на координатной плоскости некоторую полуплоскость (рис.2.1), а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называ-ется областью допустимых решений (ОДР). ОДР всегда представляет со-бой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольни-ком, неограниченной выпуклой многоугольной областью, отрезком, лу-чом, одной точкой. В случае несовместности системы ограничений задачи (1.2) ОДР является пустым множеством. [5]
Все вышесказанное относится и к случаю, когда система ограничений (1.2) включает равенства, поскольку любое равенство
можно представить в виде системы двух неравенств (см. рис.2.1)
ЦФ при фиксированном значении определяет на плоскости прямую линию . Изменяя значения L, мы полу-чим семейство параллельных прямых, называемых линиями уровня.
Это связано с тем, что изменение значения L повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси (начальная ордината), а угловой коэффициент прямой останется постоянным (см.рис.2.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.
Вектор с координатами из коэффициентов ЦФ при и перпендикулярен к каждой из линий уровня (см. рис.2.1). Направление вектора совпадает с направлением возрастания ЦФ, что является важ-ным моментом для решения задач. Направление убывания ЦФ противопо-ложно направлению вектора .
Суть графического метода заключается в следующем. По направле-нию (против направления) вектора в ОДР производится поиск опти-мальной точки . Оптимальной считается точка, через которую проходит линия уровня , соответствующая наибольшему (наименьшему) значению функции . Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоуголь-ника ОДР, через которую пройдет целевая прямая, или на всей его сто-роне. [13]
При поиске оптимального решения задач линейного программиро-вания возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оп-тиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.
Рисунок 2.1 Геометрическая интерпретация ограничений и ЦФ зада-чи.
2.1.1 Методика решения задач ЛП графическим методом.
I. В ограничениях задачи (1.2) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые.
II. Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи (1.2). Для этого нужно подставить в кон-кретное неравенство координаты какой-либо точки, например, (0;0), и проверить истинность полученного неравенства. Если неравенство истин-ное, то надо заштриховать полуплоскость, содержащую данную точку; иначе (неравенство ложное) надо заштриховать полуплоскость, не содер-жащую данную точку.
Поскольку и должны быть неотрицательными, то их допусти-мые значения всегда будут находиться выше оси и правее оси , т.е. в I-м квадранте. Ограничения-равенства разрешают только те точки, кото-рые лежат на соответствующей прямой. Поэтому необходимо выделить на графике такие прямые.
III. Определить ОДР как часть плоскости, принадлежащую одновре-менно всем разрешенным областям, и выделить ее. При отсутствии ОДР задача не имеет решений.
IV. Если ОДР – не пустое множество, то нужно построить целевую прямую, т.е. любую из линий уровня (где L – произвольное число, например, кратное и , т.е. удобное для проведения расчетов). Способ построения аналогичен построению прямых ограничений.
V. Построить вектор , который начинается в точке (0;0) и заканчивается в точке . Если целевая прямая и вектор построены верно, то они будут перпендикулярны.
VI. При поиске максимума ЦФ необходимо передвигать целевую прямую в направлении вектора , при поиске минимума ЦФ – против направления вектора . Последняя по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой точки (точек) не суще-ствует, то можно сделать вывод о неограниченности ЦФ на множестве планов сверху (при поиске максимума) или снизу (при поиске минимум).
VII. Определить координаты точки max (min) ЦФ и вычис-лить значение ЦФ . Для вычисления координат оптимальной точки необходимо решить систему уравнений прямых, на пересечении которых находится . [12]
2.2. Применение графического метода решения задачи линейного программирования на практике
Экономическая постановка задачи линейного программирования
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной тех-нологической линии. Суточный объем первой линии 60 изделий, второй линии 80 изделий. На радиоприемник первой модели расходуется 15 од-нотипных элементов электронных схем, на радиоприемник второй модели 10 таких же элементов. Максимальный суточный запас используемых элементов равен 950 единиц. Прибыли от реализации одного радиоприем-ника первой и второй моделей равны 40$ и 20$ соответственно. Определи-те оптимальные суточные объемы производства первой и второй моделей на основе графического решения задачи.
Построение математической модели
Переменные задачи. В задаче требуется установить, сколько радио-приемников первой и второй модели надо производить. Поэтому искомы-ми величинами, а значит, и переменными задачи являются суточные объе-мы производства каждого типа радиоприемников:
– суточный объем производства радиоприемников первой модели, [шт/сутки];
– суточный объем производства радиоприемников второй модели, [шт/сутки];
Целевая функция. Цель задачи — добиться максимального дохода от реализации продукции. Т.е. критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму. [2] Чтобы рассчитать величину суточного дохода от продажи радиоприемников обоих моделей, необходимо знать:
— их объемы производства, т.е. и радиоприемников в сутки;
— прибыль от их реализации — согласно условию, соответственно 40 и 20 $.
Таким образом, доход от продажи суточного объема производства радиоприемников первой модели равен $ в сутки, а от продажи ра-диоприемников второй модели – $ в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи радиоприемников первой и второй моде-ли:
[$/сутки]
Ограничения. Возможные объемы производства радиоприемников и ограничиваются следующими условиями:
— количество элементов электронных схем, израсходованное в тече-нии суток на производство радиоприемников обоих моделей, не может превышать суточного запаса этих элементов на складе;
— суточный объем первой технологической линии (производство ра-диоприемников первой модели) не может превышать 60 шт в сутки, второй (производство радиоприемников второй модели) – 80 шт;
— объемы производства радиоприемников не могут быть отрицатель-ными.
Таким образом, все ограничения задачи делятся на 3 группы, обу-словленные: расходом элементов электронных схем; суточным объемом технологических линий; неотрицательностью объемов производства.
Запишем эти ограничения в математической форме: 1.Т.к. из условия на радиоприемники первой и второй модели необходимо 15 и 20 элемен-тов соответственно, то данное ограничение имеет вид: [шт/сутки].
2.Ограничения по суточному объему первой и второй технологиче-ских линий имеют вид: [шт/сутки].
3.Неотрицательность объемов производства задается как
.
Таким образом, математическая модель этой задачи имеет вид:
2.2.1. Нахождение оптимального решения задачи с помощью линейно-го метода.
Математическую модель задачи о радиоприёмниках мы нашли на предыдущем шаге:
Построим прямые ограничений, для чего вычислим координаты то-чек пересечения этих прямых с осями координат (рис.2.2).
прямая (1) – точки (0;95) и (63,(3);0), прямая (2) проходит через точ-ку параллельно оси , прямая (3) проходит через точку параллельно оси .
Рис.2.2. Графическое решение задачи о производстве радиоприемни-ков.
Определим ОДР. Например, подставим точку (0;0) в исходное огра-ничение (1), получим , что является истинным неравенством, поэто-му стрелкой обозначим полуплоскость, содержащую точку (0;0), т.е. рас-положенную правее и ниже прямой (1). Аналогично определим допусти-мые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис.2.2). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник ABCDE.
Целевую прямую можно построить по уравнению
Точки пересечения с осями – (0;75) и (37,5;0)
Строим вектор из точки (0;0) в точку (40;20). Точка D – это по-следняя вершина многоугольника допустимых решений ABCDE, через ко-торую проходит целевая прямая, двигаясь по направлению вектора . По-этому D – это точка максимума ЦФ. Определим координаты точки D из системы уравнений прямых ограничений (1) и (2)
Получили точку D(60;5) [шт/сутки].
Максимальное значение ЦФ равно [$/сутки].
Таким образом, наилучшим режимом работы предприятия является ежесуточное производство радиоприемников первой модели в количестве 60 штук и радиоприемников второй модели в количестве 5 штук. Доход от продажи составит 2500 $ в сутки.
2.3. Анализ чувствительности оптимального решения задач ли-нейного программирования
Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. мо-жет привести к неоптимальности или непригодности прежнего режима ра-боты. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП. [3]
Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограниче-ния проходят через оптимальную точку. Несвязывающие ограничения не проходят через оптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представ-ляемый несвязывающим ограничением – недефицитным. Ограничение называют избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.
1. Анализ сокращения или увеличения ресурсов:
— на сколько можно увеличить (ограничения типа ) запас дефицит-ного ресурса для улучшения оптимального значения ЦФ?
— на сколько можно уменьшить (ограничения типа ) запас недефи-цитного ресурса при сохранении оптимального значения ЦФ?
2. Увеличение (ограничения типа ) запаса какого из ресурсов наиболее выгодно?
3. Анализ изменения коэффициентов ЦФ: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение.
2.3.1. Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)
Проанализируем чувствительность оптимального решения задачи о производстве радиоприемников. ОДР задачи (рис.2.2) – многоугольник ABCDE. В оптимальной точке D пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ре-сурсы (суточный объем элементов электронных схем и производитель-ность первой технологической линии) – дефицитными.
Рассмотрим экономический смысл этих понятий. Точка максимума ЦФ D соответствует суточному производству 60 шт радиоприемников первой модели и 5 шт радиоприемников второй модели. В производстве радиоприемников используются однотипные элементы электронных схем. Суточный запас на складе этих элементов – это правая часть связывающе-го ограничения (1) (950 шт/сутки). Согласно этому ограничению, на про-изводство в точке D расходуется [шт элементов/сутки](1).
Аналогично видим, что производительность первой технологической линии — это правая часть связывающего ограничения (2) (60 шт/сутки). Со-гласно этому ограничению в точке D данная линия производит 60 радио-приемников первой модели в сутки.
Таким образом, понятие «связывающие ограничения» (1) и (2) озна-чает, что при производстве радиоприемников в точке D(60;5) запасы эле-ментов электронных схем расходуются полностью, а так же производи-тельность первой технологической линии используется в полном объеме. По этой причине невозможно дальнейшее наращивание производства.
В этом заключается экономический смысл понятия дефицитности ре-сурсов, т.е. если предприятие сможет увеличить суточные запасы элемен-тов электронных схем или производительность первой технологической линии, то это позволит увеличить выпуск радиоприемников. В связи с этим возникает вопрос: до какого уровня целесообразно увеличить данные ре-сурсы, и на сколько при этом увеличится оптимальное производство ра-диоприемников?
Правило №1. Чтобы графически определить максимальное увеличе-ние запаса дефицитного ресурса, вызывающее улучшение оптимального решения, необходимо передвигать соответствующую прямую в направле-нии улучшения ЦФ до тех пор, пока это ограничение не станет избыточ-ным.
При прохождении прямой (1) через точку К (рис.2.3) многоугольник ABKE становится ОДР, а ограничение (1) – избыточным. Действительно, если удалить прямую (1), проходящую через точку К, то ОДР ABKE не изменится. Точка К становится оптимальной, в этой точке ограничения (2) и (3) становятся связывающими.
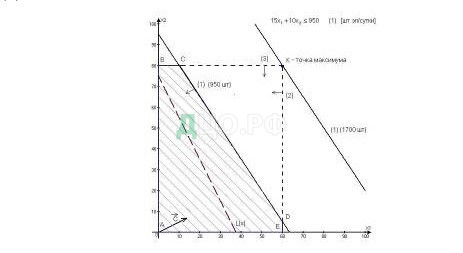
Рис.2.3. Анализ увеличения суточного запаса элементов электронных схем
Правило №2. Чтобы численно определить максимальную величину запаса дефицитного ресурса, вызывающую улучшение оптимального ре-шения, необходимо:
1) определить координаты точки , в которой соответствующее ограничение становится избыточным;
2) подставить координаты в левую часть соответствующего ограничения.
Координаты точки К(60;80) находятся путем решения системы урав-нений прямых (2) и (3). Т.е. в этой точке предприятие будет производить 60 шт радиоприемников первой модели и 80 шт радиоприемников второй модели. Подставим и в левую часть ограничения (1) и полу-чим максимально допустимый запас элементов электронных схем [шт эл/сутки].
Дальнейшее увеличение запаса элементов электронных схем нецеле-сообразно, потому что это не изменит ОДР и не приведет к другому опти-мальному решению (см. рис.2.3). Доход от продажи радиоприемников в объеме, соответствующем точке К, можно рассчитать, подставив ее коор-динаты в выражение ЦФ [$/сутки].
Рассмотрим вопрос о целесообразности увеличения производитель-ности первой технологической линии. Согласно правилу №1, соответству-ющее ограничение (2) становится избыточным в точке J, в которой пересе-каются прямая (1) и ось переменной (рис.2.4). Многоугольник ABCJ становится ОДР, а точка J (63,33;0) (или (63;0)-целочисленное решение) – оптимальным решением.
Рис.2.4. Анализ увеличения производительности первой технологи-ческой линии
В точке J выгодно производить только радиоприемники первой мо-дели (63 шт в сутки). Доход от продажи при этом составит
[$/сутки]
Чтобы обеспечить такой режим работы, согласно правилу №2, про-изводительность первой технологической линии надо увеличить до вели-чины [шт/сутки]. Ограничение (3) является несвязывающим, т.к. не проходит через оптимальную точку D (см. рис.2.5). Соответствующий ему ресурс (производительность второй технологической линии) является не-дефицитным. С экономической точки зрения это означает, что в данный момент уровень производительности второй технологической линии непо-средственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке D.
Например, увеличение (уменьшение) суточного объема второй тех-нологической линии будет соответствовать перемещению прямой ограни-чения (3) вверх (вниз). Перемещение прямой (3) вверх никак не мо-жет изменить точку D максимума ЦФ. Перемещение же прямой (3) вниз не влияет на существующее оптимальное решение только до пересечения с точкой D (см. ниже правило №3). Из рис.2.5 видно, что дальнейшее пере-мещение (3) приведет к тому, что точка D будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное реше-ние для этой новой ОДР будет хуже точки D.
Рис.2.5. Анализ уменьшения производительности второй технологи-ческой линии
Правило №3. Чтобы определить максимальное уменьшение запаса недефицитного ресурса, не меняющее оптимальное решение, необходимо передвигать соответствующую прямую до пересечения с оптимальной точ-кой. [2]
Правило №4. Чтобы численно определить минимальную величину запаса недефицитного ресурса, не меняющую оптимальное решение, необ-ходимо подставить координаты оптимальной точки в левую часть соответ-ствующего ограничения. Чтобы выяснить, до каких пределов уменьшение производительности второй технологической линии не повлияет на произ-водство в точке D, используем правило №4 Подставляем в левую часть ограничения (3) координаты точки D, получаем [шт/сутки].
Делаем вывод: предельный уровень, до которого может уменьшиться объем второй технологической линии, и при котором не изменится опти-мальность полученного ранее решения, равен 5 шт радиоприемников в сутки.
Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в таблице 2.1.
Таблица 2.1 – Результаты решения первой задачи
| № | Тип ресурса | Max
изменение ресурса, , шт/сутки |
Max
изменение дохода, , $/сутки |
Ценность
дополнительной единицы ресурса , $/шт |
| (1) | Дефицитный | 1700-950=+750 | 4000-2500=+1500 | |
| (2) | Дефицитный | 63-60=+3 | 2520-2500=+20 | |
| (3) | Недефицитный | 5-80=-75 | 2500-2500=0 |
2.3.2. Вторая задача анализа на чувствительность (увеличение запаса какого из ресурсов наиболее выгодно)
Анализ табл. 2.1 показывает, что к улучшению оптимального реше-ния, т.е. к увеличению суточного дохода приводит увеличение дефицитных ресурсов. Для определения выгодности увеличения этих ресурсов исполь-зуют понятие ценности дополнительной единицы i-го ресурса
где – максимальное приращение оптимального значения ЦФ; – максимально допустимый прирост объема i-го ресурса.
Например, из табл. 2.1 следует, что увеличение суточного запаса элементов электронных схем (ограничение (1)) на 1 шт позволит получить дополнительный доход, равный 2 $/сутки, в то время как увеличение про-изводительности первой технологической линии (ограничение (2)) на 1 шт принесет 6,7 $/сутки. Недефицитные ресурсы имеют нулевые ценности, по-скольку изменение этих ресурсов не приводит к увеличению дохода.
Вывод: дополнительные вложения в первую очередь необходимо направлять на увеличение суточного объема первой технологической ли-нии, а лишь потом на увеличение суточного запаса элементов электронных схем. Изменять недефицитные ресурсы нет необходимости.
2.3.3. Третья задача анализа на чувствительность (в каких пре-делах допустимо изменение коэффициентов целевой функции)
Изменение цен на продукцию, т.е. изменение коэффициентов ЦФ, представляется на графике вращением целевой прямой вокруг оптималь-ной точки. Так, при увеличении коэффициента ЦФ или уменьшении целевая прямая вращается по часовой стрелке. При уменьшении или же увеличении целевая прямая вращается против часовой стрелки (рис.2.6).
Рис.2.6. Анализ изменения цен
При таких поворотах точка D будет оставаться оптимальной до тех пор, пока наклон целевой прямой не выйдет за пределы, определяемые наклонами прямых ограничений (1) и (2). Так, например, если наклон це-левой прямой совпадет с наклоном прямой (1), то оптимальным решением будут точки отрезка СD. При совпадении c прямой (2) оптимальным ре-шением будут точки отрезка DE.
Наличие альтернативных оптимумов свидетельствует о том, что одно и то же оптимальное значение может достигаться при различных значени-ях переменных. Если целевая прямая выйдет за пределы наклона (1), то оптимальной точкой станет точка C. Допустим, что цена на радиоприем-ники второй модели не меняется, т.е. зафиксируем значение целевого ко-эффициента . Проанализируем графически результаты изменения значе-ния целевого коэффициента , т.е. цены на радиоприемники первой моде-ли. Оптимальное решение в точке D не будет меняться при увеличении до тех пор, пока целевая прямая не совпадет с прямой (2). Аналогично, оп-тимальное решение в точке D не будет меняться при уменьшении до тех пор, пока целевая прямая не совпадет с прямой (1).
Совпадение в процессе вращения целевой прямой с прямой ограни-чения означает, что углы их наклона относительно горизонтальной оси сравнялись, а значит, стали равны тангенсы углов наклона этих прямых.
Правило №5. Чтобы определить границы допустимого диапазона изменения коэффициента ЦФ, например и , необходимо при-равнять тангенс угла наклона целевой прямой поочередно к танген-сам углов наклона прямых связывающих ограничений, например и (рис.2.7 и 2.8).
Определим, насколько максимально может снизиться цена на радио-приемники первой модели, не изменяя оптимальную точку D. Для этого применим правило №5.
Тангенсы угла наклона для прямых L(x) и (1) соответственно равны: и .
Тогда из равенства находим [$/шт].
Рис.2.7. Определение
Рис.2.8. Определение
Теперь попробуем определить, насколько максимально может уве-личиться цена на радиоприемники первой модели, чтобы не изменилась оптимальная точка D. На рис 2.8 видно, что значение c1 можно увеличи-вать беспредельно, так как прямая L(x) при c2 = 20 и никогда не совпадает с прямой (2). Следовательно, точка D при всех значениях коэф-фициента будет единствен¬ной оптимальной.
Из приведенных выше расчетов и графической их иллюстрации сле-дует, что если цена на радиоприемники первой модели станет меньше 30 $/шт, то наиболее выгодным будет производство радиоприемников в точке C (см. рис.2.7). При этом производительность первой технологической ли-нии будет использоваться не в полном объеме, что приведет к недефицит-ности данного ресурса (2), а дефицитными будут ресурсы (1) и (3).
Проведем те же самые исследования для радиоприемников второй модели. Для этого зафиксируем значение . Ищем :
Тогда из равенства находим [$/шт]
На рис 2.8 видно, что значение c2 можно уменьшать до нуля, так как прямая L(x) при c1 = 40 и совпадает с прямой (2). Следовательно, точка D при всех значениях коэффициента будет оптимальной.
Аналогично делаем вывод, что если цена на радиоприемники второй модели станет выше 26,67 $/шт, то наиболее выгодным будет производ-ство радиоприемников в точке C.
С экономической точки зрения производство радиоприемников в точке С означает, что предприятию станет выгоднее изготовлять радио-приемники второй модели, используя на полную мощность производи-тельность второй технологической линии.
Так в данной главе настоящей курсовой работы мы рассмотрели по-строение экономико-математической задач линейного программирования, и, в частности, провели расчет по поставленной задаче с последующим экономическим анализом полученного решения, в нашем случае это ана-лиз на чувствительности.
ЗАКЛЮЧЕНИЕ
С помощью методов линейного программирования решается боль-шое количество экстремальных задач, связанных с экономикой. В этих случаях находят крайние значения (максимум и минимум) некоторых функций переменных величин.
Основой линейного программирования служит решение системы линейных уравнений, которые преобразуются в уравнения и неравенства. Оно характеризуется математическим выражением переменных величин, определенным порядком, последовательностью расчетов, логическим ана-лизом. Оно применимо: [6]
• при наличии математической определенности и количественной ограниченности между изучаемыми переменными величинами;
• при взаимозаменяемости факторов из-за последовательности расче-тов;
• в случае совмещения математической логики с пониманием сущно-сти изучаемых явлений.
В промышленном производстве этот метод помогает исчислению оптимальной общей производительности машин, агрегатов, поточных ли-ний (в случае, если задан ассортимент продукции и соответствующие вели-чины), а также решению задачи рационального использования материалов (с наиболее выгодным количеством заготовок).
В сельском хозяйстве с помощью этого метода определяют мини-мальную стоимость кормовых рационов с учетом заданного количества кормов (исходя из видов и содержащихся в них полезных веществ).
В литейном производстве данный метод помогает решить задачу о смесях, входящих в состав металлургической шихты. Этот же метод поз-воляет решить транспортную задачу, задачу наиболее оптимального при-крепления потребляющих предприятий к предприятиям, производящим продукцию.
Отличительной особенностью всех экономических задач, которые можно решить, применяя методы линейного программирования, является выбор вариантов решения, а также определенные ограничивающие усло-вия. Решение подобной задачи означает выбор наиболее оптимального из всех альтернативных вариантов. [2]
Существенной ценностью применения методов линейного програм-мирования в экономике является выбор наиболее оптимального варианта из огромного количества всех допустимо возможных вариантов. Иными способами почти невозможно решать подобные задачи, чтобы найти сте-пень рациональности использования ресурсов в производстве.
В ходе работы над курсовым проектом была рассмотрена задача ли-нейного программирования о производстве радиоприемников. Для реше-ния задачи использовался графический метод. Получены следующие ре-зультаты:
Оптимальная прибыль от реализации продукции достигается при следующем суточном производстве радиоприемников: 60 шт радиоприем-ников первой модели и 5 шт радиоприемников второй модели. При этом прибыль от реализации составит 2500$ в сутки.
Рассмотрев три задачи анализа полученного решения на чувстви-тельность к принятой модели, мы можем ответить на следующие вопросы:
1. Определите предел увеличения производительности первой ли-нии, превышение которого уже не будет улучшать значения целевой функ-ции. Предел увеличения производительности первой линии равен 63 ра-диоприемника в сутки. Дальнейшее увеличение производительности не имеет смысла, т.к. значение ЦФ не улучшится.
2. Определите предел уменьшения производительности второй линии, при котором полученное оптимальное решение останется неизмен-ным. Предельный уровень, до которого может уменьшиться производи-тельность второй технологической линии, и при котором не изменится оп-тимальность полученного ранее решения, равен 5 радиоприемников в сут-ки.
3. Определите предел увеличения суточного запаса элементов электронных схем, при превышении которого улучшить значение целевой функции оказывается невозможным. Предел увеличения суточного запаса элементов электронных схем равен 1700 шт в сутки. Дальнейшее увеличе-ние нецелесообразно, потому что это не изменит ОДР и не приведет к дру-гому оптимальному решению.
4. Определить дефицитный ресурс, который имеет наибольший приоритет при возможности увеличения запасов ресурсов. Т.к. увеличение производительности первой технологической линии на 1 шт принесет 6,7 $/сутки (в отличии от 2$/сутки от увеличения суточного запаса элементов электронных схем), то именно данный ресурс (2) имеет приоритет.
5. Определите интервал изменения прибыли от продажи радио-приемника первой модели, в котором оптимальное решение остается неиз-менным. Интервал изменения прибыли от продажи радиоприемника пер-вой модели, в котором оптимальное решение остается неизменным, опре-деляется неравенством $/шт.
6. Определите аналогичный интервал для приемника второй мо-дели. Интервал изменения прибыли от продажи радиоприемника второй модели, в котором оптимальное решение остается неизменным, определя-ется неравенством $/шт.
Решение данной задачи помогло более глубоко и основательно изу-чить и укрепить на практике все тонкости и моменты графического метода решения задач линейного программирования, а так же разобраться с ос-новами анализа на чувствительность модели к полученному оптимальному решению.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Алексеева Е.В. Построение математических моделей целочис-ленного линейного программирования. Примеры и задачи: Учеб. пособие / Новосибирский государственный университет., Новосибирск, 2012. 131 с.
2. Алесинская Т.В. Учебное пособие по решению задач по курсу» Экономико-математические методы и модели». Таганрог: Изд-во ТРТУ, 2012, 153 с.
3. Астафуров В.Г., Колодникова Н.Б. Компьютерное учебное по-собие, раздел “Анализ на чувствительность с помощью двойственной за-дачи”, Томск — 2012, 98 с.
4. Гладких Б.А. Методы оптимизации и исследование операций для бакалавров информатики. Ч. III. Теория решений: учебное пособие. — Томск: Изд-во НТЛ, 2012 — 281 с.
5. Вентцель Е.С. Исследование операций. Задачи, принципы, ме-тодология. М.: КноРус, 2012, 182 с.
6. Веремеенко Т. В. Высшая математика: учебно-методическое пособие. В 4 ч. Ч. 4 Математическое программирование / 2-е изд., испр. – Минск: ГИУСТ БГУ, 2012 – 158 с.
7. Демидов К.В., Духанов А.В. Теория игр и исследование опера-ций. Курс лекций. Учебное издание/ Владимирский государственный уни-верситет, 2012. — 59 с.
8. Конюховский П.В. Математические методы исследования опе-раций в экономике — СПб.: Издательство «Питер», 2012. — 208 с.
9. Лемешко Б.Ю. Теория игр и исследование операций: Конспект лекций / – Новосибирск: Изд-во НГТУ, 2013 – 129 с.
10. Мамаева З.М. Линейные экономико-математические модели. Учебно-методическое пособие. / Нижний Новгород: ННГУ, 2012.-72 с.
11. Надеждин Е.Н., Смирнова Е.Е., Варзаков В.С. Математические методы и модели в экономике: учебное пособие для студентов экономиче-ских специальностей. — Тула: Автономная некоммерческая организация ВПО «Институт экономики и управления», 2011 — 249 с.
12. Орлова, И.В. Экономико-математические методы и модели: компьютерное моделирование / Вузовский учебник: ИНФРА-М, 2011 368 с.
13. Черноиванова, Е.А. Исследование операций и методы оптими-зации: курс лекций, учеб. пособие/ Саранский кооперативный институт РУК. – Саранск: Принт-Издательство, 2014 – 132 с.
