Вид работы: Лабораторная работа
Дисциплина: Электротехника
Тема: «Исследование линейной разветвленной цепи постоянного тока»
Вариант 3
- Цель работы. Проверить выполнение законов Кирхгофа, принципов наложения и взаимности, теоремы о линейных соотношениях.
- Схема электрической цепи
- Ответы на вопросы по подготовке к работе
1)Как выбирать контуры, чтобы уравнения Кирхгофа для них оказались взаимно независимыми?
Ответ:Для любой цепи взаимно независимые уравнения для напряжений получаются, если, записав уравнение для любого контура, мысленно разорвать в нем одну ветвь, а следующие уравнения, также с разрывом ветви, записывать для оставшихся целых контуров до их исчерпания.
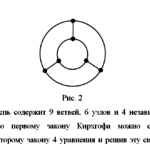
2)На рис. 2 дана структурная схема некоторой цепи (ветви изображены линиями, узлы – точками). Определить для нее число взаимнонезависимых уравнений, которые можно составить по первому и второму законам Кирхгофа.
Рис. 2
Ответ: Данная цепь содержит 9 ветвей, 6 узлов и 4 независимых контура, следовательно, по первому закону Кирхгофа можно составить 6-1=5 уравнения, а по второму закону 4 уравнения и решив эту систему линейных уравнений, можно найти токи в девяти ветвях.
3) На рис. 3 изображена исследуемая цепь без измерительных приборов и ключей. Записать для нее необходимое число взаимно независимых уравнений по законам Кирхгофа.
Рис. 3
Ответ:
Составим уравнения для данной схемы
Решив эту систему линейных уравнений можно найти все неизвестные токи в трех ветвях.
4) Каковы правила знаков при записи уравнений Кирхгофа?
Ответ:По первому закону Кирхгофа сумма приходящих и отходящих от узла токов равна нулю. Приходящие токи берутся с одним, определенным знаком, а отходящие токи – с противоположным.
По второму закону Кирхгофа для контура, сумма падений напряжения на резисторах равна сумме напряжений источников ЭДС. Если направление обхода контура совпадает с направлением тока, то падение напряжения берется со знаком плюс, если не совпадает, то со знаком минус. Если направление действия ЭДС совпадает с направлением обхода контура, то ЭДС берется со знаком плюс, если не совпадает, то со знаком минус.
5)В чем сущность принципа наложения? Как его проверить на примере цепи рис.1
Ответ:Принцип наложения. Ток любой ветви линейной электрической цепи с несколькими источниками может быть представлен в виде алгебраической суммы составляющих от действия каждого источника в отдельности. Для того чтобы определить токи методом наложения на Рис.1, надо рассчитать все токи от действия Е1, закоротив при этом зажимы Е2. Потом рассчитать все токи от действия Е2, закоротив Е1. А затем надо алгебраически сложить одноименные токи.
6) Поясните принцип взаимности применительно к цепи рис. 3 и выведите формулы для аналитической его проверки (доказать тождество выражений для двух токов).
Ответ:
Принцип взаимности. Принцип взаимности. Если в пассивной линейной цепи выделитьдве ветви abи cd, в одну из них включить ЭДС Еab= Е, а в другой измерить ток Icd= I, затем переставить ту же ЭДС во вторую ветвь (Еcd= Е),а ток измерить в первой, то эти два тока окажутся равными (Iab= I).
Таблица 1.1
| Опыт | ЭДС | Показания приборов | Результаты вычислений | |||||
| Е1 | Е2 | I1 | I2 | I3 | ƩIR(1) | ƩIR(2) | ƩI | |
| B | B | мA | мA | мA | B | B | мA | |
| 1 | 6 | 0 | 34,4 | -14,7 | -19,7 | 6 | 0 | 0 |
| 2 | 0 | 6 | -14,7 | 49,2 | -34,4 | 0 | 6 | 0 |
| 3 | 6 | 6 | 19,7 | 34,4 | -54,1 | 6 | 6 | 0 |
| Расчет | 6 | 6 | 19,7 | 34,5 | -54,1 | Проверка принципа наложения | ||
Таблица 1.2
| Номер опыта | U1 | U2 | I2 | I3 | Примечание |
| B | B | мА | мА | ||
| 4 | 6 | 6 | 34,4 | -54,1 | I3=aI2+b a=1,331 b=-99,88 |
| 3 | 6 | 6 | 34,4 | -54,1 | |
| 2 | 0 | 6 | 49,2 | -34,4 |
Опыт № 5. Проверка принципа взаимности.
Таблица 1.3
| Опыт | Показания приборов | Расчет | ||||
| U1 | U2 | I1 | I2 | I1 | I2 | |
| B | B | мА | мА | мА | мА | |
| 2 | 0 | 6 | -14,7 | — | -14,7 | — |
| 5 | 6 | 0 | — | -14,7 | — | -14,7 |
- Пояснение к таблицам 1.1, 1.2, 1.3, показывающие справедливость законов или соотношений, а также примеры расчетов строки или столбца.
4.1. Результаты первых трех опытов сведены в таблицу 1. 1. В этойтаблице проверяется справедливость принципа наложения. Первая и вторая строки этой таблицы отражают справедливость первого закона Кирхгофа, а третья и четвертая строки – справедливость принципа наложения
Расчет первой строки
Расчет второй строки
Расчет третьего столбца
Справедливость второго закона Кирхгофа (Первая строка таблицы 1.1, опыт № 1, для первого контура)
Справедливость второго закона Кирхгофа (Первая строка таблицы 1.1, опыт № 1, для второго контура)
То есть справедливость второго закона Кирхгофа выполняется. Аналогично можно составить уравнения для второй и третьей строки.
4.2. Результаты опытов 2, 3 и 4 внесены в таблицу 1.2. В этой таблице проверяется теорема о линейном соотношении токов I2 и I3.
На основании опытов 3 и 2 составим систему линейных уравнений
Подставим численные значения опытов
Решив эту систему линейных уравнений с двумя неизвестными, получим
Проверим величину тока I3 в четвертом опыте
То есть теорема о линейном соотношении токов I2 и I3 выполняется.
4.3 Принцип взаимности (Таблица 1.3). Если в пассивной линейной цепи выделить две ветви, в одну из них включить ЭДС, а в другой измерить ток, затем переставить ту же ЭДС во вторую ветвь, а ток измерить в первой, то эти два тока окажутся равными.
Произведем расчет тока I2 в пятом опыте (вторая строчка таблицы 1.3). Рассчитаем входное сопротивление схемы (Рис 1.5) относительно первой ветви, где включен источник Е1
Величина тока I1
Падение напряжения на второй и третьей ветвях
Величина тока во второй ветви
То есть принцип взаимности соблюдается.
Произведем расчет тока I1 вовтором опыте (первая строчка таблицы 1.3). Рассчитаем входное сопротивление схемы (Рис 1.2) относительно второй ветви, где включен источник Е2
Величина тока I2
Падение напряжения на первой и третьей ветвях
Величина тока в первой ветви
То есть принцип взаимности и здесь соблюдается.
Выводы
По первому закону Кирхгофа сумма приходящих и отходящих от узла токов равна нулю. Приходящие токи берутся с одним, определенным знаком, а отходящие токи – с противоположным.
По второму закону Кирхгофа для контура, сумма падений напряжения на резисторах равна сумме напряжений источников ЭДС. Если направление обхода контура совпадает с направлением тока, то падение напряжения берется со знаком плюс, если не совпадает, то со знаком минус. Если направление действия ЭДС совпадает с направлением обхода контура, то ЭДС берется со знаком плюс, если не совпадает, то со знаком минус.
Принцип наложения. Ток любой ветви линейной электрической цепи с несколькими источниками может быть представлен в виде алгебраической суммы составляющих от действия каждого источника в отдельности
Принцип взаимности. Если в пассивной линейной цепи выделитьдве ветви, в одну из них включить ЭДС, а в другой измерить ток, затем переставить ту же ЭДС во вторую ветвь, а ток измерить в первой, то эти два тока окажутся равными.
Лабораторная работа № 3.
Вариант № 3
Конденсатор и катушка индуктивности в цепи синусоидального тока
Цель работы. Научиться определять параметры конденсатора и катушки индуктивности с помощью амперметра, вольтметра и фазометра, строить векторные диаграммы, а также проверить выполнение законов Кирхгофа в цепи синусоидального тока.
Ответы на вопросы
1 Реальный конденсатор обладает активной проводимостью g (из-за несовершенства изоляции в конденсаторе), и емкостью С. В схемах замещения конденсатор обычно представляется параллельной схемой этих составляющих. Катушка индуктивности тоже имеет индуктивную L и активную R составляющие, которые в схемах замещения обычно представляют последовательной цепочкой этих составляющих.
- Активная, емкостная, индуктивная, реактивная, полная проводимости — это величины, обратные сопротивлениям: активному, емкостному, индуктивному, реактивному и полному. Между собой они связаны следующими соотношениями
Полная проводимость конденсатора
Активная проводимость конденсатора
Емкостная проводимость конденсатора
- Активное, емкостное, индуктивное, реактивное, полное сопротивления — это величины, которые определяют величины сопротивления переменному току.
Между собой они связаны следующими соотношениями:
- Угол сдвига фаз между напряжением и током на входе двухполюсника может меняться от минус 900 до плюс 900. Причем ток отстает от напряжения при индуктивной нагрузке и опережает при емкостной.
Уравнение первого закона для данной схемы
Для этой схемы уравнение второго закона Кирхгофа
- Соберем схему своего варианта (вариант 3)
Рис. 2.1
2.1. Разомкнем ключ 1, включим питание (Рис. 2.1) и запишем показания приборов в таблицу 2.1
Таблица 2.1
| Данные опыта | Результаты расчета | ||||||||||
| U | I | φ | I1 | I2 | C | g | δ | İ | İ1 | İ2 | İ |
| B | A | град | А | А | мкФ | См | град | А | А | А | А |
| 100 | 1,43 | -87,9 | — | 1,43 | 45 | 0,0005 | -2,1 | 1,43 | — | 1,43 | 1,43 |
| 99,8 | 2,20 | -40 | 1,63 | 1,43 | 45 | 0,0005 | -2,1 | 1,63 | |||
Полная проводимость конденсатора
Активная и реактивная проводимости конденсатора
Полная проводимость в комплексном виде в алгебраической и показательной формах
Угол потерь конденсатора
Величина тока в цепи
Данные расчетов занесем в таблицу 2.1
1.4. Замкнем ключ и с помощью реостата установим угол сдвига фазы напряжения и тока φ1=-400 (Рис. 2.2)
Рис. 2.2
Показания приборов внесем в нижнюю строку таблицы 2.1.
1.5. Определим все токи расчетным путем
Сопротивление первой ветви
Проводимость первой ветви
Общая проводимость первой и второй ветви
Определим комплексное сопротивление первой и второй ветвей
Величина общего тока цепи
Определим токи в первой и второй ветвях
Проверим правильность расчетов по первому закону Кирхгофа
Расчеты произведены правильно, некоторые расхождения обусловлены погрешностью при округлениях.
1.6. Используя данные таблицы построим диаграмму токов (Рис 2.3).
Вектор напряжения совпадает с горизонтальной осью. Вектор тока первой ветви практически совпадает с приложенным напряжением. Вектор тока второй ветви опережает вектор напряжения на 87,90. Убеждаемся, что алгебраическая сумма двух ветвей равна общему току.
Исследование активно-индуктивной цепи
2.1. Собираем схему (Рис 2.4).
2.2. Сопротивление реостата устанавливаем равным нулю и данные приборов записываем в таблицу 2.2
Таблица 2.2
| U | I | φ | U1 | U2 | L | R | QL | Ů | Ů1 | Ů2 | ƩŮ |
| В | А | град | В | В | Гн | Ом | — | В | В | В | В |
| 100 | 0,749 | 72,3 | 0 | 100 | 0,4 | 40,6 | 3,13 | — | 0 | — | — |
| 100 | 0,509 | 40,0 | 55,9 | 67,9 | — | — | — | 55,9 |
2.3. Модуль полного сопротивления катушки
Активное и индуктивное сопротивление катушки
Индуктивность и добротность катушки
Данные расчетов занесем в таблицу 2.2
2.4. При помощи реостата устанавливаем угол сдвига фаз напряжения и тока на входе согласно третьего варианта φ2=400 (Рис 2.5) и запишем показания приборов в таблицу 2.2.
Рис. 2.5
2.5. Сделаем расчет падений напряжения на реостате и на катушке индуктивности. Примем начальную фазу входного тока равной нулю.
Сопротивление реостата
Падение напряжения на реостате
Падение напряжения на катушке индуктивности
Общее сопротивление цепи
Величина входного напряжения
Подсчитаем сумму падений напряжений на реостате и катушке индуктивности
По данным второй строки таблицы 2.2 построим топографическую диаграмму напряжений (Рис 2.6)
Вектор падения напряжения на реостате по направлению совпадает с вектором тока и численно равен 55,9 В. вектор падения напряжения на катушке опережает вектор тока на 72,30 и численно равен 68,0 В. Убеждаемся, что алгебраическая сумма этих двух векторов равна приложенному напряжению.
- Выводы
При параллельном соединении нагрузок алгебраическая сумма токов в параллельных ветвях равна току в неразветвленной ее части. При последовательном соединении нагрузок алгебраическая сумма падений напряжения на каждой из нагрузок равна приложенному напряжению.
Прикрепленные файлы:
Прикрепленные файлы: |
|
|---|---|

|
Администрация сайта не рекомендует использовать бесплатные работы для сдачи преподавателю. Эти работы могут не пройти проверку на уникальность. Узнайте стоимость уникальной работы, заполните форму ниже: Узнать стоимость |

|
Скачать файлы: |
|
|
|