Математическая модель системы с выбором на обслуживание. Часть 2.

Страницы:   1   2

---

2. Одноканальная система поллинга с двумя потоками заявок

2.1. Описание системы с бесконечным накопителем

 

В этой части рассматривается система поллинга с простейшим порядком опроса очередей.

Рассмотрим одноканальную систему массового обслуживания, на вход которой поступает два потока заявок. Поток заявок первого типа является пуассоновским с параметром λ₁, поток заявок второго типа является пуассоновским с параметром λ₂.

Время обслуживания заявки каждого типа на приборе имеет экспоненциальное распределение с параметрами μ₁ и μ₂ соответственно.

Накопители для заявок первого и второго типа бесконечные.

Переключение прибора между очередями первого и второго типа происходит мгновенно.

Выбор заявки на обслуживание происходит по следующей схеме: выбирается заявка из очереди большей длины. Если же длины очередей для заявок первого и второго типа одинаковы, то выбор на обслуживания заявки первого типа происходит с вероятностью q, а заявки второго типа с вероятностью 1-q. Такой дисциплины обслуживания нет в классификации систем поллинга, в этом и состоит главная новизна этой работы.

Схема такой системы массового обслуживания изображена на рисунке 2.1.

 

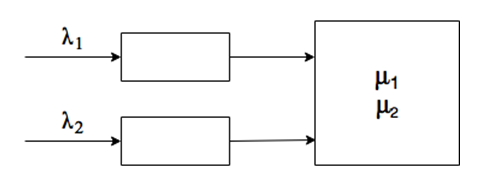
Схема поллинга.

Введем следующий процесс, описывающий функционирование системы:

n1^(t) — число заявок первого типа в очереди в момент времени t,

n2^(t) — число заявок второго типа в очереди в момент времени t

 — тип заявки, обслуживаемый на приборе.

Тогда определим марковский процесс V^t следующим образом:

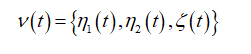
Процессы n1^(t) и n2^(t) принимают значения из множества {0, 1, 2…},  принимает значения из множества {1, 2}.

Обозначим через

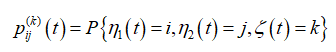
вероятность того, что в системе в момент времени t в накопителе для заявок первого типа – i заявок, в накопителе для заявок второго типа – j заявок, k – тип заявки, который обслуживается на приборе. Дополнительно обозначим через  — вероятность того, что момент времени t в системе нет очереди и нет обслуживаемых заявок.

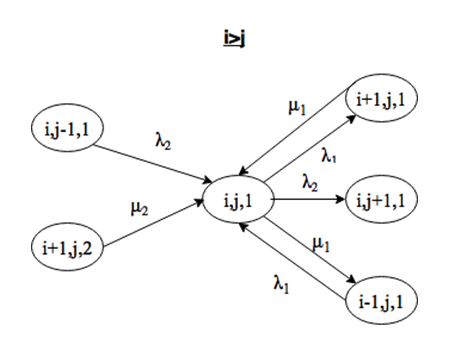
Для составления уравнений глобального баланса (УГБ) рассмотрим фрагменты переходов между состояниями системы:

Система находится в состоянии (i, j, 1), причем i>=j. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 типа на приборе. Войти в состояние (i, j) можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 или 2 типов, причем переход возможен только из состояния (i+1, j, k), так как на обслуживание выбирается заявка из накопителя с большей длиной (рис. 2.2 и 2.3).

 

 

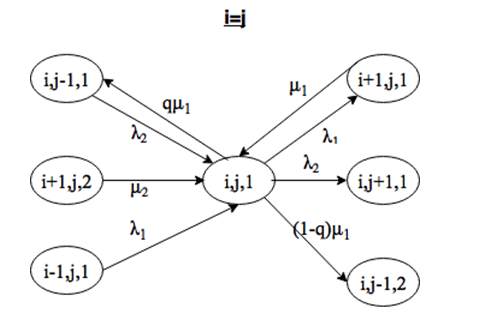
Система находится в состоянии (i, j, 1), причем i=j-1. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 типа на приборе. Войти в состояние (i, j) можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 или 2 типов, причем переход возможен только из состояния (i+1, j, k) с вероятностью q, так как при равной длине очереди заявка на обслуживание выбирается случайно с помощью вероятности (рис. 2.4).

 

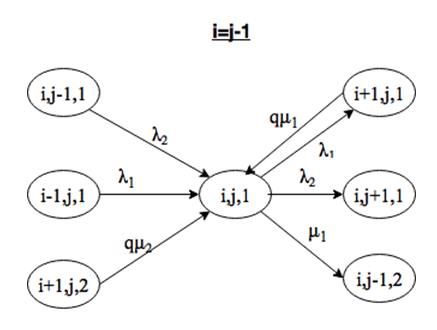
Система находится в состоянии (i, j, 1), причем i<j-1. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 типа на приборе. Войти в состояние (i, j) можно при поступлении заявки интенсивности λ₁ или λ₂, нельзя войти за счет окончания обслуживания, так как количество заявок второго типа больше, и на обслуживание должны выбираться только они (рис. 2.5).

 

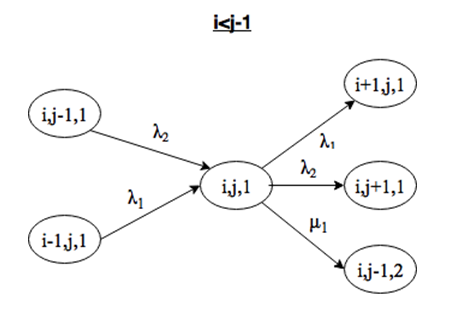
Система находится в состоянии (i, j, 2), причем j>=i. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 2 типа на приборе. Войти в состояние (i, j) можно при поступлении заявки интенсивности λ₁ или λ₂, либо за счет окончания обслуживания заявки 1 или 2 типов, причем переход возможен только из состояния (i, j+1, k), так как на обслуживание выбирается заявка из накопителя с большей длиной (рис. 2.6 и 2.7).

 

 

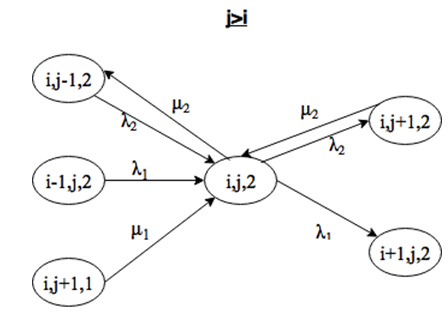
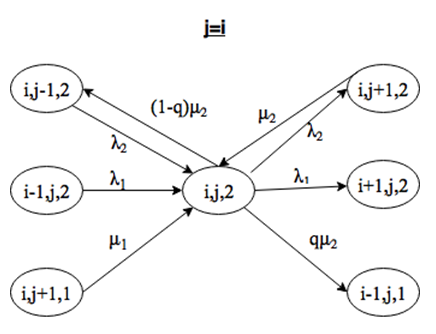
Система находится в состоянии (i, j, 2), причем j=i-1. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 2 типа на приборе. Войти в состояние (i, j) можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 или 2 типов, причем переход возможен только из состояния (i, j+1, k) с вероятностью q, так как при равной длине очереди заявка на обслуживание выбирается случайно с помощью вероятности (рис. 2.8).

 

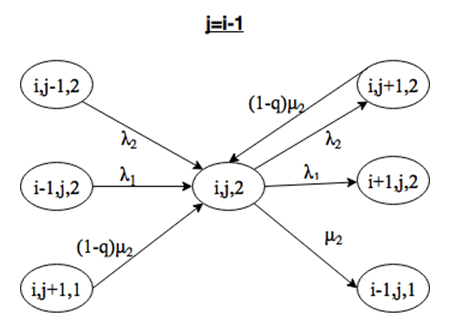
Система находится в состоянии (i, j, 2), причем j<i-1. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 2 типа на приборе. Войти в состояние (i, j) можно при поступлении заявки интенсивности λ₁ или λ₂, нельзя войти за счет окончания обслуживания, так как количество заявок первого типа больше, и на обслуживание должны выбираться только они (рис. 2.9).

 

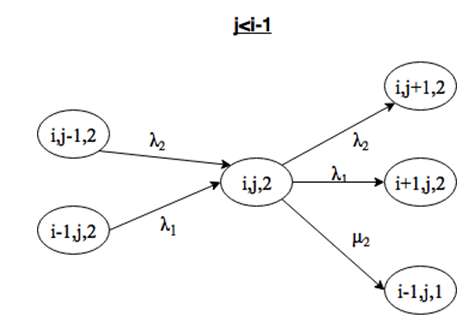
Система находится в состоянии (i, 0, 1), причем i>=2. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 типа на приборе. Войти в состояние (i, 0) можно при поступлении заявки интенсивности λ_1, либо за счет окончания обслуживания заявки 1 или 2 типов, причем переход возможен только из состояния (i+1, 0, k) (рис. 2.10).

 

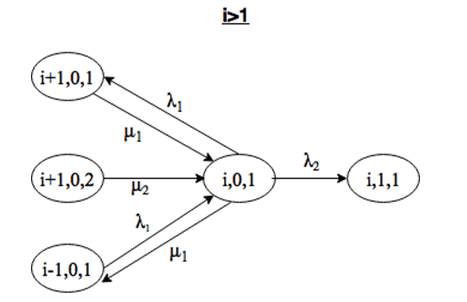
Система находится в состоянии (i, 0, 2), причем i>=2. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 2 типа на приборе. Войти в состояние (i, 0) можно только при поступлении заявки интенсивности λ₁, нельзя войти за счет окончания обслуживания, так как количество заявок первого типа больше, и на обслуживание должны выбираться только они (рис. 2.11).

 

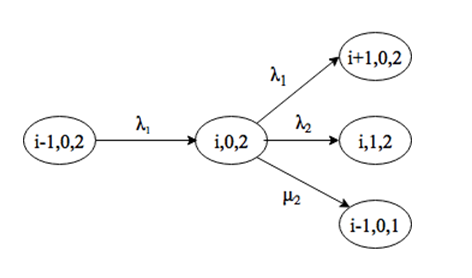
Система находится в состоянии (0, j, 1), причем j>1. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 типа на приборе. Войти в состояние (0, j) можно при поступлении заявки интенсивности λ_2, либо за счет окончания обслуживания заявки 1 или 2 типов, причем переход возможен только из состояния (0, j+1, k) (рис. 2.12).

 

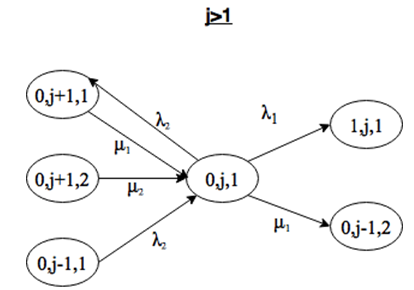
Система находится в состоянии (0, j, 2), причем j>1. Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 2 типа на приборе. Войти в состояние (0, j) можно только при поступлении заявки интенсивности λ₂, либо за счет окончания обслуживания заявки 1 или 2 типов (рис. 2.13).

 

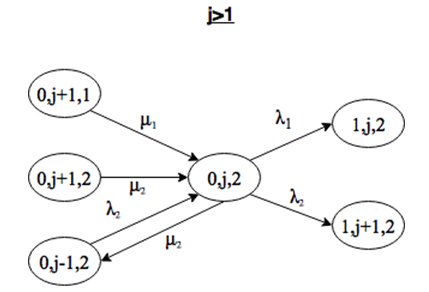
Система находится в состоянии (1, 0, 1). Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 типа на приборе. Войти в состояние (1, 0, 1) можно только при поступлении заявки интенсивности λ₁, либо за счет окончания обслуживания заявки 1 или 2 типов (рис. 2.14).

 

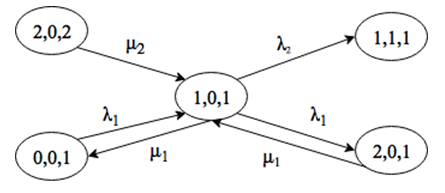
Система находится в состоянии (1, 0, 2). Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 2 типа на приборе. Войти в состояние (1, 0, 2) можно только при поступлении заявки интенсивности λ₁, либо за счет окончания обслуживания заявки 1 или 2 типов (рис. 2.15).

 

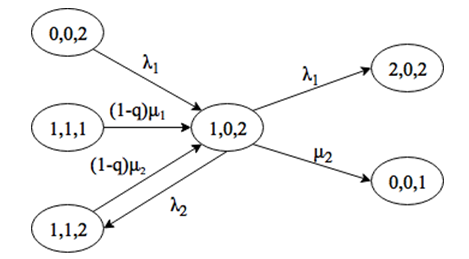
Система находится в состоянии (0, 1, 1). Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 типа на приборе. Войти в состояние (0, 1, 1) можно только при поступлении заявки интенсивности λ₂, либо за счет окончания обслуживания заявки 1 или 2 типов (рис. 2.16).

 

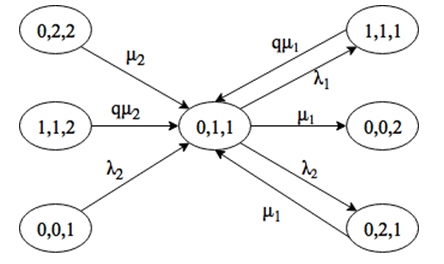
Система находится в состоянии (0, 1, 2). Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 2 типа на приборе. Войти в состояние (0, 1, 2) можно только при поступлении заявки интенсивности λ₂, либо за счет окончания обслуживания заявки 1 или 2 типов (рис. 2.17).

 

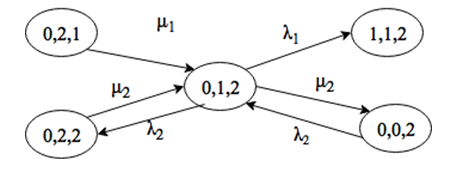
Система находится в состоянии (0, 0, 1). Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 1 типа на приборе. Войти в состояние (0, 0, 1) можно только при поступлении заявки интенсивности λ₁, либо за счет окончания обслуживания заявки 1 или 2 типов (рис. 2.18).

 

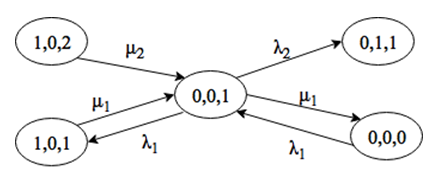
Система находится в состоянии (0, 0, 2). Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ_2, либо за счет окончания обслуживания заявки 2 типа на приборе. Войти в состояние (0, 0, 2) можно только при поступлении заявки интенсивности λ₂, либо за счет окончания обслуживания заявки 1 или 2 типов (рис. 2.19).

 

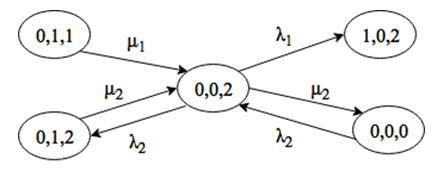
Система находится в состоянии (0, 0, 0). Выйти из этого состояния можно при поступлении заявки интенсивности λ₁ или λ₂. Войти в состояние (0, 0, 0) можно только при поступлении заявки интенсивности λ₁ или λ₂ (рис. 2.20).

 

Обозначим через

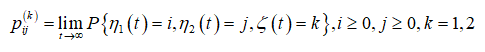
стационарные вероятности того, что в очереди i заявок первого типа, j заявок второго типа, и на приборе обслуживается заявка типа k. Через

обозначим стационарную вероятность, того, что в системе нет никаких заявок.

Условия существования стационарного режима для такой системы будет такое же, как и для системы массового обслуживания:

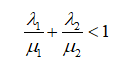
Учитывая рассмотренные выше фрагменты графа интенсивностей переходов между состояниями, получим систему уравнений глобального баланса.

Если добавить к этой системе еще одно нормировочное уравнение для вероятности всех состояний, то эти соотношения будут полностью определять вероятности состояний системы в стационарном режиме.

Эта система уравнений представляет собой определенные сложности для исследования. Такая простая дисциплина опроса очередей превращается в 17 уравнений, из которых получить явные выражения для всех вероятностей состояний невозможно.

Основные стационарные характеристики системы.

Обозначим через Q₁ и Q₂ среднюю длину очереди для первого и второго типа заявок. Их можно вычислить по следующим формулам:

 

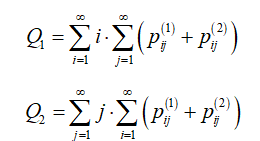
2.1. Частные случаи

 

Частный случай системы с совпадающими интенсивностями входящих потоков

Предположим, что интенсивности поступления первого и второго потоков совпадают и равны λ. Тогда систему уравнений можно переписать:

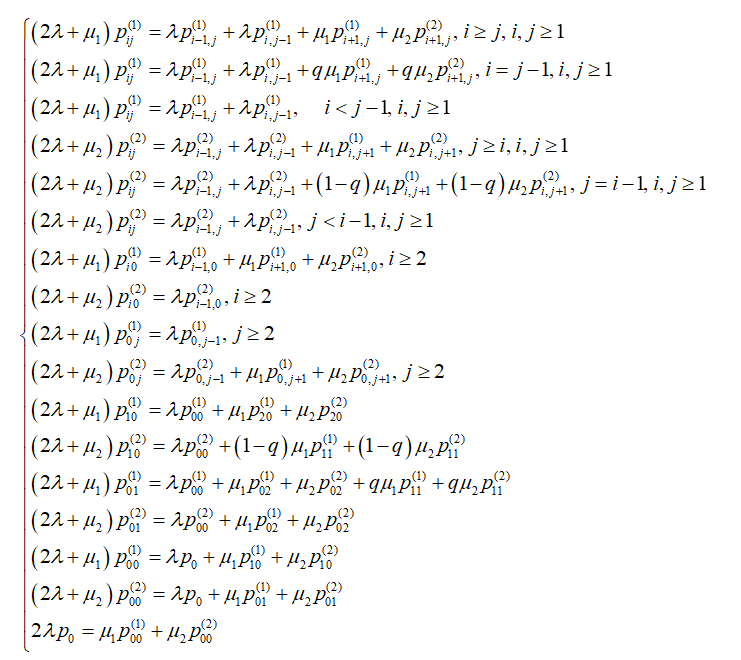
• Частный случай системы с совпадающими интенсивностями обслуживания

Предположим, что интенсивности обслуживания потоков первого и второго типов совпадают и равны μ.

Тогда можно рассмотреть упрощенную модель, в которой не важно, какой вызов обслуживается на приборе, так как вероятности перехода из одного состояния системы в другое от этого не зависят.

Введем следующий процесс, описывающий функционирование системы:

n1^(t) — число заявок первого типа в накопителе в момент времени t,

n2^(t) — число заявок второго типа в накопителе в момент времени t.

Тогда определим марковский процесс следующим образом:

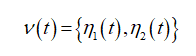
Процессы n1^(t) и n2^(t) принимают значения из множества {0, 1, 2…}.

Обозначим через

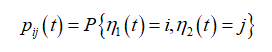
вероятность того, что в очереди в момент времени t находится i заявок первого типа и j заявок второго типа. Через p0^(t) обозначим вероятность того, что в системе нет заявок ни в очереди, ни на обслуживании. А через p00^(t) обозначим вероятность того, что в очередях нет заявок, но одна заявка (не важно какого типа) обслуживается на приборе.

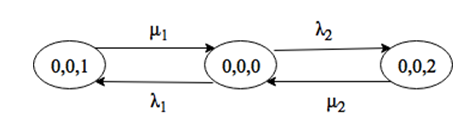
Тогда граф состояний системы будет иметь вид:

 

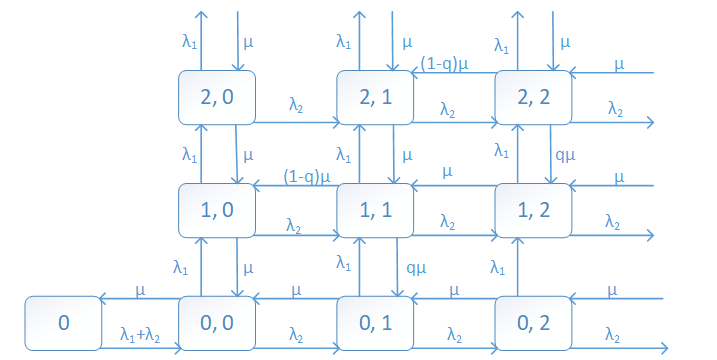
По этому графу состояний получим систему уравнений глобального баланса:

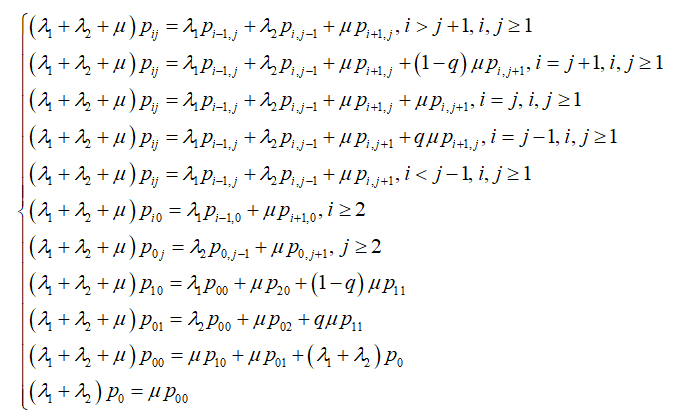
Найдем стационарное распределение числа заявок в системе и в накопителе.

Обозначим через p_k вероятность того, что в системе k заявок, не важно какого типа. Если наблюдать систему только в моменты поступления заявок или окончания их обслуживания, то получим обычный процесс гибели-размножения. Для такого процесса известно выражение для вероятностей p_k

где ρ определяется следующим образом

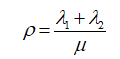
Если ρ <1 (условие существования стационарного режима), то можно найти производящую функцию числа заявок в системе:

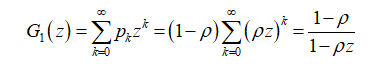
С помощью этой функции найдем среднее число заявок в системе

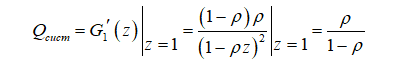
Обозначим через p_k` вероятность того, что в накопителе находится k заявок. Эта вероятность связана с вероятностью p_k соотношением

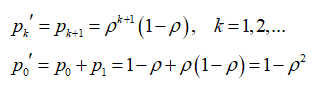
Найдем также производящую функцию числа заявок в накопителе

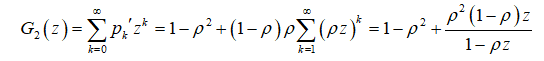
С помощью этой функции найдем среднее число заявок в накопителе

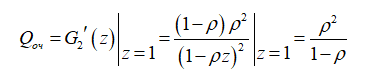
Частный случай системы с совпадающими интенсивностями входящих потоков и интенсивностями обслуживания

Предположим, что интенсивности поступления первого и второго потоков совпадают и равны λ, также интенсивности обслуживания потоков первого и второго типов совпадают и равны μ.

Тогда систему уравнений получается из системы уравнений из частного случая системы с совпадающими интенсивностями обслуживания.

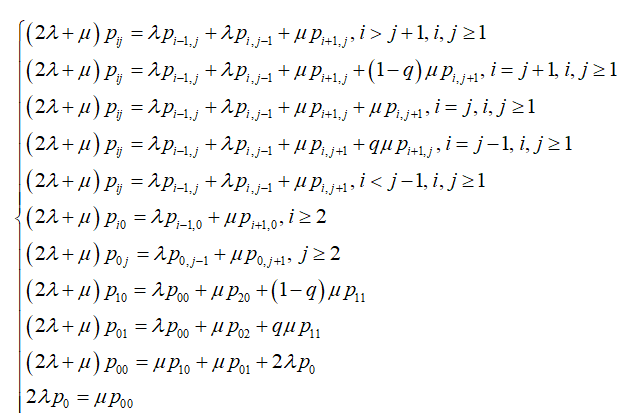
Как и в предыдущем пункте определим вероятности того, что в системе находится k заявок и в очереди находится k заявок по аналогичным формулам

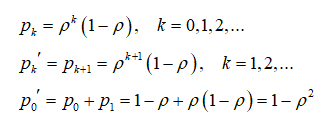
Единственное отличие в том, что ρ определяется по формуле

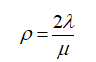
Тогда производящие функции количества заявок в системе и накопителе будут иметь точно такой же вид

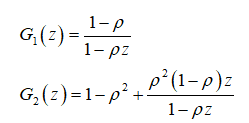
И среднее количество заявок в системе и накопителе будет равно

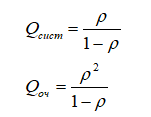
Рассмотрим пример. В накопителе находится 5 заявок, то есть может быть в одной очереди 5 заявок, а другая пустая, или в первой очереди 1 заявка, а в другой – 4 заявки, и так далее. Вероятность того, что в очереди находится ровно 5 заявок можно найти как сумму вероятностей:

С другой стороны, эту вероятность можно найти с помощью уже выведенной формулы:

Для заданных интенсивностей поступления заявок и обслуживания, эта вероятность определяется однозначно.

 

Заключение

 

Теорию массового обслуживания следует рассматривать как раздел прикладной математики, изучающей процессы, связанные с удовлетворением массового спроса на выполнение какого-либо вида услуг с учетом случайного характера спроса и обслуживания. Применительно к электроэнергетике это могут быть задачи: формирования резервного фонда электрооборудования, работа ремонтного персонала по ликвидации аварийных ситуаций в электроустановках, производство переключений и подготовка рабочих мест в электрических сетях оперативным персоналом, оценка надежности восстанавливаемых систем и т. д.

Каждая система массового обслуживания (СМО) может быть представлена в виде определенного числа обслуживающих единиц, которые называются каналами обслуживания (термин взят из телефонных сетей, применительно к которым начала развиваться теория массового обслуживания). В качестве канала могут рассматриваться различного вида приборы и приспособления, вычислительная машина, коллектив людей или отдельный исполнитель, выполняющий определенный вид работ. По числу каналов СМО делится на одноканальные и многоканальные системы.

Функционирование любой СМО заключается в обслуживании поступающего в нее потока заявок или требований. Заявки обычно поступают нерегулярно, образуя случайный поток заявок (требований). На обслуживание заявки также необходимо определенное время. Случайный характер потока заявок и времени обслуживания приводит к неравномерной загрузке СМО. В какие-то периоды времени скапливается большое количество заявок (они либо становятся в очередь, либо покидают СМО, не получив обслуживания), в другие периоды СМО может работать с недогрузкой или простаивать.

В практической деятельности довольно часто приходиться сталкиваться с системами, в которых заявка, поступившая в систему в любой момент времени, может застать канал занятым обслуживанием. Характерным с этой точки зрения является работа сетей передачи данных при возникновении ситуации сбоя или другой нештатной ситуации (климатические нагрузки, перегрузка сети, т.д.). Повреждение, как случайное событие, может произойти в любой момент времени, на любой отходящей линии, а может произойти одновременно на нескольких линиях передачи данных. Поскольку повреждения, возникающие в разных местах, сразу устранить невозможно, то необходимо предусмотреть вероятности возникновения отказов и своевременно принять меры для их предупреждения.

Исходя из вышеизложенного, в качестве СМО выбрана система с ожиданием, в которой заявка, заставшая все каналы занятыми, становится в очередь и ожидает своего обслуживания неограниченное количество времени. Проведены соответствующие расчеты для системы. При рассмотрении таких систем следует учитывать такие характеристики как средняя длина очереди, время пребывания заявки в очереди и т. д.

 

Список литературы

 

1. Вишневский В.М. Теоретические основы проектирования компьютерных сетей. – М.: Техносфера, 2003
2. Вишневский В.М., Семенова О.В. Системы поллинга: теория и применение в широкополосных беспроводных сетях. – М.: Техносфера, 2007
3. Vishnevsky, O.Semenova. “Polling Systems: Theory and Applications for Broadband Wireless Networks”. London: LAMBERT Academic Publishing, 2012
4. Takagi, H. «Queuing analysis of polling models». ACM Computing Surveys, 1988.
5. Takahashi Y., Fujimoto K., Makimoto N., “Geometric decay of the steady-state probabilities in a quasi-birth-and-death process with a countable number of phases”, Commun. in Stat.: Stochastic Models, 2001
6. Самуйлов К. Е., Абаев П.О., Гайдамака Ю.В., Гудкова И.А., Королькова А. В., Кулябов Д.С., Щукина О.Н. Мультисервисные сети связи. – М.: РУДН, 2013
7. Lee T., Sunjaya J. “Exact analysis of asymmetric random polling systems with single buffers and correlated Levy input process”, Queueing Syst. 1996
8. Dou C., Chang J.-F. “Serving two correlated queues with a synchronous server under exhaustive service discipline and nonzero switchover time”, IEEE Trans. Commun. 1991
9. Stavrakakis I., Tsakiridou S. “Study of class of partially ordered service strategies for a system of two discrete-time queues”, Performance Evaluat. 1997
10. Назаров А.А., Уразбаева С.У. Исследования декомпозированной модели многопакетного режима сети с протоколом DQDB. – Вестник Томского государственного университета, 2002
11. Назаров А.А., Уразбаева С.У. Исследования систем массового обслуживания в дискретном времени и их применение к анализу оптоволоконных сетей связи. – АиТ, 2002
12. Takahashi Y., Kumar B.K. “Pseudo-conservation law for discrete-time multi-queue system with priority disciplines”, J. Oper. Res. Soc. Japan, 1995
13. Levy H., Kleinrock L. Polling systems with zero switch-over periods: A general method for analysis the expected delay”, Performance Evaluat. 1991
14. Boxma O.J., Groenendijk W.P., Weststrate J.A. “A pseudoconservation law for service systems with a polling table”, IEEE Trans. Commun. 1990
15. Tassiulas L., Ephrimides A. “Dynamic server allocation to parallel queues with randomly varying connectivity”, IEEE Trans. Inform. Theory. 1993
16. Browne S., Kella O. “Parallel service with vacations”, Oper. Res. 1995
17. Cooper R.B., Niu S.-C., Srinavasan M.M. “Setups in polling models: does it make sense to set up if no work is waiting?”, J. Appl. Prob. 1999
18. Ibe O.C. “Analysis of polling systems with mixed service discipline”, Commun. in Stat.: Stochastic Models, 1990
19. Shiozawa Y., Takine T., Takahashi Y., Hasegawa T. “Analysis of a polling system with correlated input”, Computer Networks and ISDN Syst. 1990
20. Chang W., Down D.G. “Exact asymptotics for k_i-limited exponential polling models”, Queueing Syst. 2002
21. Boxma O.J., Schlegel S., Yechiali U. “Two-queue polling models with a patient server”, Ann. Oper. Res. 2002
22. Feng W., Kowada M., Adachi K. “A two-queue model with Bernoulli service schedule and switching times”, Queueing Syst. 1998
23. Lee D.-S., Sengupta B. “Queuing analysis of a threshold based priority scheme for ATM networks”, IEEE Transactions on Networking 1993
24. Lee D.-S. “A two-queue model with exhaustive and limited service discipline”, Commun. in Stat.: Stochastic Models, 1996
25. Eliazar I., Fibich G., Yechiali U. “A communication multiplexer problem: two alternating queues with dependent randomly-timed gated regime”, Queueing Syst. 2005
26. Feng W., Kowada M., Adachi K. “Performance analysis of a two-queue model with an (M, N)-threshold service schedule”, J. Oper. Res. Soc. Japan, 2001
27. van der Heijden M.C., Harten A., Ebben M.J.R. “Waiting times at periodically switched one-way traffic lanes – A periodic, two-queue polling system with random setup times”, Prob. Engineering Inform. Sci. 2001
28. Chakravarthy S.R., Thiagarajan S. “Two parallel finite queues with simultaneous services and markovian arrivals”, J. Appl. Math. Stochastic Anal. 1997
29. Coffman E.G., Jr., Puhalskii A.A., Reiman M.I. “Polling systems in heavy traffic: a Bessel process limit”, Math. Oper. Res. 1998
30. Jirachiefpattana A., County P., Dillon T.S., Lai R. “Performance Evaluate of PC routers using a single-server multi-queue system with a reflection technique”, Comput. Commun. 1997
31. Srinavasan M.M., Niu S.-C., Cooper R.B. “Relating polling models with nonzero switchover times”, Queueing Syst. 1995
32. Günalay Y., Gupta D. “Threshold start-up control policy for polling systems”, Queueing Syst. 1998
33. Sharma V. “Stability and continuity of polling systems”, Queueing Syst. 1994
34. Baba Y. “Analysis of batch arrival cyclic service multiqueue systems with limited service discipline”, J. Oper. Res. Soc. Japan, 1991
35. Eliazar I. “Gated polling systems with Levy inflow and inter-dependent switchover times: a dynamical-systems approach”, Queueing Syst. 2005
36. Leung K.K. “Cyclic service systems with probabilistically-limited service”, IEEE J. Selected Areas Commun. 1994
37. Levy H. “Analysis of cyclic polling systems with binomial-gated service”, Performance of Distributed Parallel Syst. Amsterdam, Elsevier Science Publishers B.V. 1989
38. Levy H. “Binomial-gated service: a method for effective operation and optimization of polling systems”, IEEE Trans. Commun. 1991
39. Tedijanto T.E. “Exact results for the cyclic-service queue with a Bernoulli schedule”, Performance Evaluat. 1990
40. Chiarawongse J., Srinivasan M.M. “On pseudo-conversation laws for the cyclic server system with compound Poisson arrivals”, Oper. Res. Lett. 1991
41. Ibe O.C., Trivedi K.S. “Two queues with alternating service and server breakdown”, Queueing Syst. 1990
42. Hwang L.-C., Chang C.-J. “An exact analysis of an asymmetric polling system with mixed service discipline and general service order”, Comput. Commun. 1997
43. Rubin I., Tsai Z. “Performance of token schemes supporting delay constrained priority traffic streams”, IEEE Trans. Commun. 1990
44. Fournier L., Rosberg Z. “Expected waiting times in cyclic service systems under priority disciplines”, Queueing Syst. 1991
45. Takagi H. “Analysis of an M|G|1|N queue with multiple server vacations, and it application to a polling model”, J. Oper. Res. Soc. Japan, 1992
46. Гаврилов А.Ф., Красильников Ю.П. Циклическое обслуживание с прямой информационной связью. – АиТ, 1976
47. de Souza e Silva E., Gail R.H., Muntz R.R. “Polling systems with server timeouts and their application to token passing networks”, IEEE/ACM Transactions on Networking. 1995
48. Eliazar I., Yechiali U. “Pollling under the randomly-timed gated regime”, Commun. in Stat.: Stochastic Models. 1998
49. van der Mei R.D., Levy H. “Polling systems in heavy traffic: Exhaustiveness of service policies”, Queueing Syst. 1997
50. Gupta D., Srinivasan M.M. “Polling systems with state-dependent setup times”, Queueing Syst. 1996
51. Langaris C. “A polling model with retrial customers”, J. Oper. Res. Soc. Japan. 1997
52. Саксонов В.В. Исследование многоканальной замкнутой циклической системы массового обслуживания. – АиТ, 1979
53. Eisenberg M. “The polling system with a stopping server”, Queueing Syst. 1994
54. Frigui I., Alfa A.S. “Analysis of a discrete time table polling system with MAP input and time-limited service discipline”, Telecommunication Syst. 1999
55. Landry R., Stavrakakis I. “Queueing study of 3-priority policy with distinct service strategies”, IEEE/ACM Transactions on Networking. 1993

---

Страницы:   1   2