Методы решения планиметрических и основы решения стереометрических задач в школьном курсе геометрии. Часть 2

1 2

---

 

Глава 2. Методы решения планиметрических задач

В типологии математических задач, представленной в [1 с. 103] одним из первых рассматривается деление их по признаку математического содержания.

Если условие и заключение задачи принадлежат определенному разделу математики, то она принадлежит одному из следующих типов — арифметические, алгебраические, геометрические, тригонометрические, комбинаторные и т. д.

Геометрические задачи составляют в этой типологии отдельный класс задач, специфические особенности которых мы и рассмотрим.

2.1 Геометрическая задача: понятие, структура, решение

Одной из важнейших характеристик овладения математикой на том или ином уровне является умение решать задачи, причем не только стандартные, но и «требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности» [17 с. 16].

Говоря о геометрической задаче, напомним некоторые положения общей теории задач в обучении математике, конкретизируя их, где это возможно и целесообразно, на задачах геометрического характера.

Примем следующее понятие задачи: задача — это требование или вопрос, на который надо найти ответ, опираясь на те условия, которые указаны в задаче, и/или учитывая их [23 с. 6].

Математическая задача — это задача, сформулированная на математическом языке, а геометрическая задача — это задача, сформулированная на геометрическом языке.

Иногда задача формулируется на житейском, бытовом или профессиональном языке нематематической отрасли знаний, но решается математическими (геометрическими) средствами. Тогда прежде чем решать, ее надо перевести на математический (геометрический) язык.

Такого рода задачи очень важны в процессе формирования компетенций. Однако они очень редко встречаются в учебниках математики (геометрии) или в сборниках математических (геометрических) задач.

Иногда условием задачи называют всю формулировку задачи, т.е. все условия и требования вместе. В задаче обычно присутствует не одно условие, а несколько независимых элементарных (т.е. нерасчленимых далее) условий. Требований в задаче также может быть не одно.

Задача. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 см. и 12 см. Найти катеты треугольника.

В этой задаче можно выделить такие элементарные условия:

1) треугольник, о котором идет речь в задаче, прямоугольный;

2) в этот треугольник вписана окружность;

3) точка касания окружности с гипотенузой делит ее на два отрезка;

4) длина одного из этих отрезков равна 5 см.;

5) длина другого отрезка равна 12 см.

Требование этой задачи можно расчленить на два элементарных:

1) найти длину одного катета треугольника;

2) найти длину другого катета треугольника.

Понятие «решение задачи» используется в нескольких основных смыслах:

— решение задачи как план (способ, метод) осуществления требований задачи;

— решение задачи как процесс выполнения плана, реализации требования;

— решение задачи как результат выполнения плана решения.

2.2 Роль и функции геометрических задач

Роль и функции задач в обучении геометрии в основной школе во многом определяются целью изучения курса геометрии в VII-IX классах, которая сформулирована а программах по математике следующим образом: «Целью изучения курса геометрии в VII-IX классах является систематическое изучение свойств геометрических фигур на плоскости, формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин (физика, черчение и т.д.) и курса стереометрии в старших классах» [8 с. 8].

В качестве обучающей цели курса геометрии VII-IX классов в программах по математике является систематическое изучение свойств геометрических фигур на плоскости; в качестве развивающей цели — формирование пространственных представлений и развитие логического мышления; пропедевтическая цель состоит в подготовке аппарата, необходимого для изучения смежных дисциплин и стереометрии. Геометрические задачи эффективно способствуют достижению всех сформулированных в программе целей курса геометрии VII-IX классов.

Систематическое решение задач способствует сознательному и прочному усвоению теории геометрии, помогает увидеть ее практическую ценность, формирует ключевые компетенции в области геометрии.

Геометрические задачи, как и другие математические задачи, выполняют воспитательные, развивающие и обучающие функции.

Осуществляя подбор задач для урока, учитель может преследовать различные цели, используя различные функции той или иной задачи на различных этапах урока.

Задача может предварять какое-либо теоретическое положение и помогает отыскать его или усмотреть некоторую геометрическую зависимость. Тогда в задачи включают отдельные элементы доказательства теоремы. Рассмотрим пример.

Пример. Перед доказательством признака равенства треугольников по трем сторонам можно предложить следующие задачи:

а) Дано:

Доказать:

б) Дано: в четырехугольнике АBCD:

Доказать:

Решение задачи может служить источником получения новых знаний по геометрии. Тогда полезно к условию задачи сформулировать некоторую последовательность заданий-требований.

Задача. Через точку М внутри круга проведены две хорды и . Доказать, что треугольники и подобны

Последовательность заданий-требований может быть такая:

— Записать пропорциональность сходственных сторон.

— Сравнить произведение отрезков хорды CD, на которые их делит точка М.

— Провести диаметр через точку М и сравнить произведение отрезков диаметра с произведениями отрезков каждой из хорд, проходящих через точку М.

— Сформулировать полученное предложение.

Задача по геометрии может выполнять роль демонстрации практической значимости геометрии.

Задача. Длина тени, отбрасываемой деревом, равна 8,7 м, в то время как длина тени палки, воткнутой вертикально в землю, равна 1,2 м. Определить высоту дерева, если длина палки равна 0,88 м.

2.3 Классификации геометрических задач

В методической литературе приняты следующие условные классификации геометрических задач.

1. По специфике языка. В курсе геометрии основной школы часто решаются текстовые задачи, т.е. те задачи, условие которых представлено преимущественно на естественном языке. Примером такого рода задачи из задач, рассмотренных в предыдущем пункте, может служить задача о хордах круга. Как видно из этого примера, кроме естественного здесь может использоваться и геометрический язык.

Иногда решаются и сюжетные геометрические задачи, то есть те, в которых присутствует фабула.

В них описан «некоторый жизненный сюжет (явление, событие, процесс) …» [2 с. 3]. Чаще всего это геометрические задачи с практическим содержанием.

Сюжетные геометрические задачи играют значительную роль в процессе обучения, т.к. при их решении решается одна из важнейших задач всего курса математики — обучение методу моделирования и, в первую очередь, перевод естественного языка на язык математический, что иногда представляет значительную трудность.

Абстрактные задачи (с использованием только геометрического языка) встречаются гораздо реже. Иллюстрацией такого рода задач могут служить две задачи на готовых чертежах в первом из рассмотренных в предыдущем пункте примере.

2. По характеру рассматриваемых в геометрической задаче объектов они подразделяются на чисто геометрические задачи и практические задачи.

В чисто геометрических задачах речь идет только о геометрических фигурах вне связи их с конкретными объектами окружающего мира. Именно такие задачи составляют основное содержание задачного материала современных учебников геометрии.

В практических задачах основными объектами являются предметы окружающего мира. Эти задачи помогают учащимся узнавать в предметах окружающего мира знакомые геометрические фигуры, использовать те или иные свойства этих фигур и тем самым осознавать возможности практического применения геометрии.

Практические задачи играют большую роль в формировании общих компетенций. Задач с практическим содержанием в учебниках обычно недостаточно.

3. Геометрические задачи, для решения которых в школьном курсе имеются готовые алгоритмы или эти алгоритмы непосредственно следуют из определений или теорем, называют стандартными.

Стандартными являются геометрические задачи, в которых теоремы могут служить алгоритмами решения. Так, теорема о средней линии трапеции служит алгоритмом для решения задач нахождения длины средней линии трапеции по ее основаниям. Последовательность шагов алгоритма для решения таких задач проста:

1) устанавливаем длину оснований трапеции;

2) находим их полусумму. Это и будет длина средней линии.

Все так называемые элементарные задачи на построение являются стандартными.

4. Наиболее распространенная классификация, которая обычно используется и в работе с учащимися, — это классификация, основанием которой является характер требований задачи.

В соответствии с этим основанием геометрические задачи условно классифицируются на задачи: 1) на вычисление, 2) на доказательство, 3) на построение (конструктивные задачи).

Эта классификация, несмотря на очень широкое ее распространение, достаточно условна: задача на вычисление часто является и задачей на доказательство, так как требует обоснования; одним из очень существенных этапов решения задачи на построение является доказательство; во многих задачах сочетается построение, вычисления и измерение. Все же эта классификация облегчает рассмотрение особенностей каждого вида геометрических задач.

В методической литературе специально выделяются так называемые “задачи на готовых чертежах”. Далее мы кратко их охарактеризуем. Функции этих задач не столько математические, сколько методические.

Методический характер носит и классификация, основой которой является характер использования задачи на уроке. В соответствии с этой классификацией можно выделить:

— подготовительные задачи,

— задачи на раскрытие содержания новых понятий,

— задачи на применение отдельной теоремы, формулы и др.;

— комбинированные задачи: на применение нескольких теорем, формул.

Рассмотрим методику использования в процессе обучения наиболее интересных с методической точки зрения классов геометрических задач.

Методические особенности обучения решению геометрических задач

Чертеж и краткая запись условия геометрической задачи

Основная особенность геометрических задач состоит в том, что их решение практически всегда сопровождается на том или ином этапе (иногда на нескольких) построением схематического чертежа-наброска, или, в некоторых случаях, полноценного чертежа. Правильное выполнение простейшего чертежа, как и его чтение, — одни из важнейших компетенций, необходимых каждому человеку в его повседневной, а во многих случаях и профессиональной деятельности.

С методической точки зрения чертеж — важнейшее средство наглядности, значение которого для обучения геометрии трудно переоценить. Особенно значительную роль играют чертежи в курсе геометрии основной школы, так как они, в отличие от старших классов, достаточно легко выполнимы и отражают истинное положение фигуры на плоскости.

При построении чертежа следует выполнять ряд требований. Сформулируем основные из них.

1. Чертеж должен представлять собой схематический рисунок основного объекта задачи (геометрической фигуры, или совокупности фигур, или какой-то части этих фигур).
2. Все элементы фигуры и некоторые ее характеристики должны быть обозначены на чертеже с помощью букв и других знаков.

Если в тексте задачи указаны какие-либо обозначения фигуры или ее элементов, то эти обозначения должны быть и на чертеже; если же в тексте никаких обозначений нет, то следует воспользоваться общепринятыми или наиболее удобными в данном конкретном случае.

3. Чертеж к геометрической задаче должен отражать наиболее общий случай вида и расположения основного ее объекта.

Это означает, что если в задаче в качестве основного объекта назван, например, треугольник и при этом не указан его вид, то следует построить разносторонний непрямоугольный треугольник. Или если в задаче основным объектом является трапеция, то не следует строить равнобедренную или прямоугольную трапецию и т.д.

4. При выполнении чертежа желательно соблюдать заданные в условии пропорции в построении отдельных элементов фигуры.

Это не значит, что необходимо строго выдерживать масштаб. Однако, если по условию задачи сторона АВ треугольника АВС наибольшая, то это должно быть соблюдено на чертеже. Или если задана медиана треугольника, то она должна проходить через одну из вершин и приблизительно через середину противоположной стороны. Надо соблюдать также такие заданные в условии задачи отношения, как параллельность, перпендикулярность и т.п.

5. Чертеж существенно облегчит процесс решения задачи, если он верен, легко выполним, нагляден.

Построение чертежа, как правило, сопровождает краткая запись всех условий и требований геометрической задачи. В ней, пользуясь принятыми на чертеже обозначениями, записываются все характеристики и отношения, указанные в условии задачи.

При этом названия фигур или отдельных ее частей следует заменять схематической записью их определений. Так, вместо того, чтобы писать, что ABCD — трапеция, лучше записать, что ABCD.

В краткой записи, так, где это возможно и целесообразно, следует использовать стандартный математический символический язык, т.е. знаки =, ∥

Задача. Диагональ трапеции перпендикулярна к ее основаниям; тупой угол, прилежащий к ее основанию, равен 120, а боковая сторона, прилежащая к нему, равна 7 см; большее основание равно 12 см. Найти среднюю линию трапеции.

Основной объект задачи — трапеция, в которой одна из диагоналей перпендикулярна ее основаниям.

Наиболее оптимальный путь — построение этой диагонали, которую можно представить в качестве вертикального отрезка, от концов которого строятся два горизонтальных отрезка, — основания трапеции, направленные в разные стороны от диагонали. Строим тупой (по условию) угол при большем (обычно нижнем) основании. Вторая его сторона пересечет меньшее основание в одной из вершин трапеции. Достраиваем трапецию, придерживаясь заданных пропорций, проводим в ней среднюю линию, вводим стандартные обозначения тупого угла при большем основании.

2.4 Методика обучения решению стандартных геометрических задач

Стандартные геометрические задачи — это такие задачи, которые решаются с помощью одной теоремы, одного определения геометрического понятия и т.п. Тем не менее, не всегда процесс решения такой задачи проходит гладко. Дело в том, что в конкретной теореме, определении конкретной геометрической фигуры алгоритм применения их к определенной стандартной геометрической задаче находится в свернутом виде. Для того, чтобы его использовать, следует развернуть этот алгоритм в пошаговую программу действий. К тому же стандартные задачи являются основными геометрическими задачами, поскольку все остальные в конечном счете сводятся к ним.

Можно выделить следующие особенности процесса решения стандартных геометрических задач.

1. Анализ стандартной геометрической задачи сводится к распознаванию вида задач, к которому принадлежит данная задача, т.е. того общего положения геометрии (аксиомы, теоремы, определения геометрической фигуры), с помощью которого она решается.

Это диктует необходимость для обучаемого держать в оперативной памяти все изученные в геометрии общие положения — аксиомы, теоремы, определения геометрических фигур

2. Поиск решения стандартной геометрической задачи состоит в составлении на основе общего положения геометрии последовательности шагов решения задач данного вида, то есть в разворачивании свернутой в общем положении программы деятельности. Ее не обязательно формулировать письменно, достаточно просто наметить.
3. Решение стандартной геометрической задачи состоит в применении этой программы к условиям данной задачи.
4. При этом какой-то шаг программы может быть ранее решенной стандартной задачей. Таким образом, процесс накопления стандартных задач во многом индивидуален.

Пример. Для решения элементарной задачи на построение треугольника по трем элементам (сторонам и углам), каждая из которых является стандартной, используются такие ранее решенные элементарные стандартные задачи, как построение угла и отрезка, равных заданным.

2.5 Метод дополнительных построений (конструктивный)

Суть метода дополнительных построений заключается в том, что чертеж к задаче дополняется новыми (вспомогательными) элементами, после чего эти связи становятся очевидными.

Существуют задачи, в которых дополнительное построение определяет единственный способ решения.

В других задачах используется смешанный прием решения, когда дополнительное построение реализует лишь часть решения.

В третьих задачах оно применяется как один из возможных методов наряду с другими. Во многих случаях применение дополнительного построения делает решение задачи устным.

Пример задачи, представленной в ГИА, которая решается с помощью дополнительного построения:

Задача

В окружности с центром  О  проведены две равные хорды АВ и СD. На эти хорды опущены перпендикуляры  ОК  и ОL соответственно.

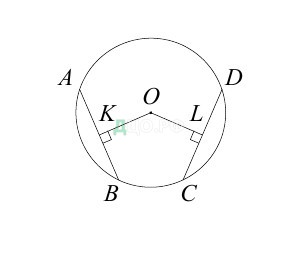
Докажите, что  ОК и ОL равны.

Решение:

Проведём радиусы ОА, ОВ, ОС, ОD. Треугольники АОВ и СОD равны по трём сторонам. ОК и ОL — их высоты, проведённые к равным сторонам, следовательно, они равны как соответственные элементы равных треугольников.

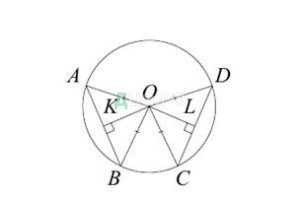
Классификация дополнительных построений, связанная с характерными признаками фигуры, данной в задаче.

Дополнительное построение 1

Если в треугольнике задана медиана, то треугольник достраивается до параллелограмма с центром в основании этой медианы (рис.1).

В зависимости от содержания задачи такое достраивание можно выполнять для одной, двух или даже трех медиан. При этом возможно использование не всего параллелограмма, а лишь его части (например, треугольника).

Задача

Две стороны треугольника равны 27 и 29, а медиана, проведенная к третьей стороне равна 26. Найти высоту, проведенную к стороне 27.

Дано:

ABC, AB=27,BC=29,BO=26 CD – высота, BO- медиана

Найти CD.

Решение:

1. Дополнительное построение: строим OE=BO, ABCE-параллелограмм (по признаку) BC=AE=29, AB=EC=27
2. =
3. = (по формуле Герона)=270

=

=,

Ответ: 20

Дополнительное построение 2

Если дана трапеция, то ее диагональ или боковая сторона параллельно переносятся (рис.2).

Задача

Найти высоту равнобедренной трапеции, если её диагонали взаимно перпендикулярны, а площадь трапеции равна S.

Дано:

ABCD — равнобедренная трапеция

AC и BD – диагонали ACBD

S — площадь трапеции

Найти: — высоту трапеции

Решение:

1. Дополнительное построение: строим
2. равнобедренный (т.к
3. прямоугольный (т.к
4. Проводим высоту — она является медианой и биссектрисой

= (

(т.к — параллелограмм)

Ответ:

Задача

Длина треугольника выражается формулой

; где — длины медиан треугольника. Докажите.

Доказательство

Отметим на медиане точку пересечения медиан треугольника; согласно свойству (три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении , считая от вершины треугольника), она делит в отношении

Продолжим на расстояние DF=OD=1/3 и соединим точку с и

Теперь составим уравнение, связывающее длины сторон BO=2/3, =2/3 и диагоналей =2/3, параллелограмма

+= 2+)

что и требовалось доказать.

Дополнительное построение 3

Если в задаче дана длина всех трёх медиан, то для того чтобы найти площадь треугольника, продолжают все медианы на 1/3 её длины и достраивают до параллелограмма.

Задача

Медианы треугольника ABC  =3см, =4см, C=5 см.

Найти площадь треугольника ABC

Решение

Продолжим медианы   и на длину отрезков равные по длине , , соответственно получим шесть равновеликих треугольников стороны которых равны 2/3 длины медиан.

=

=+=+ =

=3=

=8cм

Ответ 8 cм

Дополнительное построение 4 

Если дан четырехугольник, у которого суммы противоположных сторон равны, то в него вписывается окружность.

Задача

В трапеции ( и основания) меньшее основание равно углы, прилежащие к этому основанию, равны, а диагонали взаимно перпендикулярны. Найти площадь трапеции.

Дано:

ABCD — трапеция

AB и CD — основания

Найти S трапеции

Решение:

1. Дополнительное построение: строим описанную окружность (т.к трапеция равнобедренная, то можно описать окружность)
2. Sтр.=
3. Пусть

4.По теореме Пифагора:

По теореме Пифагора из

 

По теореме Пифагора из AQD:

8. S=

Ответ: [8]

2.6 Аналитические методы

Один из основных аналитических методов решения планиметрических задач является векторный метод.

Примерная схема решения геометрических задач векторным методом:

— Прочитать задачу, выделить условие и требование задачи, выполнить чертёж.

— Ввести в рассмотрение векторы (выбрать базис — два неколлинеарных вектора на плоскости, три некомпланарных вектора в пространстве).

— Перевести геометрическое условие задачи на язык векторов.

Векторы, необходимые для решения, выразить через базисные.

— Перевести геометрическое требование задачи на язык векторов (можно устно).

— С помощью векторной алгебры (преобразований векторных выражений) перейти от векторного условия задачи к требованию.

-Полученному векторному выражению дать геометрическое истолкование.

Пример одного из заданий, основанного на данном методе:

 

 

Задача

На катетах прямоугольного треугольника с прямым углом построены квадраты и Точка середина гипотенузы . Доказать, что отрезки и перпендикулярны.

К аналитическому методу относиться метод координат.

Примерная схема решения геометрических задач методом координат:

— Прочитать задачу, выделить условие и требование задачи, выполнить чертёж.

— Выбрать систему координат (наиболее рациональным способом).

— Записать координаты точек, необходимых для решения. «Перевести» геометрическое условие задачи на язык координат.

— Перевести геометрическое требование задачи на язык координат (можно устно).

— С помощью алгебраических преобразований перейти от условия задачи к требованию.

— Полученному алгебраическому выражению дать геометрическое истолкование.

Пример одного из решений, основанного на данном методе:

Задача

В прямоугольном равнобедренном треугольнике проведены медианы острых углов. Вычислите косинус угла между ними.

Решение:

1. Введем систему координат так, в этом случае вершины треугольника будут иметь координаты: С(0,0), А(а,0), В(0,а), а середины катетов: .

(Здесь а — длина катета.)

2. Вычислим координаты векторов и .
3. Теперь используем формулу для вычисления косинуса угла между векторами. (Этот угол совпадает с углом между медианами.)

Ответ: .

Данные методы решения планиметрических задач помогут учащимся наиболее продуктивно подготовится к решению модуля «Геометрия».

Ученик должен ознакомиться с определенным набором достаточно трудных геометрических задач, научиться решать задачи, следуя известным образцам.

В геометрии, в отличие от алгебры, алгоритмов очень мало, почти нет. Поэтому при обучении возрастает значение опорных задач.

 

2.7 Вспомогательные задачи

А) Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине.

Б) Где лежит центр окружности, описанной около прямоугольного треугольника, и чему равен ее радиус?

В) Выразить радиус вписанной окружности через гипотенузу и катеты прямоугольного треугольника.

Г) Выразить высоту, проведенную к гипотенузе, через гипотенузу и катеты.

Применение вспомогательных задач

1. Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то треугольник – прямоугольный.
2. В треугольнике АВС из вершин А и В проведены высоты, О – середина стороны АВ. Доказать, что отрезки, соединяющее основания высот с точкой О, равны.
3. В параллелограмме из вершины тупого угла проведены высоты, О – точка пересечения диагоналей параллелограмма. Доказать, что отрезки, соединяющие точку О с основаниями высот, равны.
4. В ромб, который делится своей диагональю на два равносторонних треугольника, вписана окружность радиуса r. Найти сторону ромба.
5. Вот треугольник непростой:

В нем угол АВС – прямой.

А теперь – условий узы:

с – длина гипотенузы,

r – величина не меньшей нужности –

Радиус вписанной окружности.

Задача, посильная для школьника –

Найти площадь треугольника!

Решение

Задача А:

Дополняем треугольник до прямоугольника и используем свойство его диагоналей. Задача В является следствием задачи А, в ней используется определение окружности и определение окружности, описанной около треугольника.

Задача В (рис. 1)

По свойству касательных, проведенных к окружности из одной точки,

Четырехугольник – квадрат, сторона которого равна

Задача Г.

Площадь прямоугольного треугольника можно найти двумя способами: (рис.2).

При решении задачи №1 следует обратиться к задаче А (это обратные задачи).

Достроим треугольник АВС до параллелограмма (рис.3).

Диагонали параллелограмма точкой пересечения делятся пополам, но в нашей задаче половинки АО = ВО = СО, тогда АВ = CD, а это признак прямоугольника, поэтому угол АСВ равен 900.

Задача (рис. 4)

Доказать, что  ОК = OH.

По условию О – середина АВ, значит ищи медиану или медианы.

– медиана в треугольнике , – медиана в треугольнике , поэтому

 

Задача (рис. 5).

Доказать, что ОН = ОМ.

Найдите прямую связь этой задачи с задачей №2.

Задача

Ищем ответы на вопросы:

1) где лежит центр вписанной окружности?

2) Почему в ромб можно вписать окружность?

3) Где провести радиус?

4) Каковы свойства диагоналей ромба?

Решение:

Гипотенуза прямоугольного треугольника (сторона ромба), катеты и , высота, проведенная к гипотенузе –  ; = ( +)/2;

Ответ:

Задача (рис. 6).

При решении этой задачи надо вспомнить все, связанное с площадью треугольника, радиусом вписанной окружности и гипотенузой.

Итак, вспоминаем:

необходимо как-то связать произведение чисел и их сумму . 

Вспомним формулы сокращенного умножения: (a + b)2 = a2 + b2 + 2ab;

(2r + c)2 = c2  + 2ab; 2ab = 4r2 + 4rc + c2 – c2;

ab = 2r2 + 2rc; ab/2 = r2 + rc = S.

Ответ:    S = r2 + rc.

 

2.8 Проблемные методы решения стереометрических задач

Проблемные методы решения стереометрических задач – это продуктивные методы, направленные на развитие у обучающихся, прежде всего, метапредметных компетенций.

Если при репродуктивных методах обучения обучающиеся получают мало стимулов для осуществления учебной деятельности, то при продуктивных методах поле таких стимулов значительно расширяется. При традиционных подходах к обучению учитель создает искусственную образовательную среду, которая является очень неустойчивой. Действительно, в такой среде активность обучающихся во многом обусловлена исключительно внешней мотивацией («ты должен знать, потому что от тебя это требуется», «ты должна уметь, чтобы получить хорошую отметку», «не будешь учить – не сдашь экзамен» и т.д.). Вынужденная активность, не развивая познавательный интерес, быстро сходит на нет, как только обучающийся выходит из искусственно созданной образовательной среды. Нередко облучающиеся забывают, что они проходили на уроке уже со звонком на перемену. Поэтому учителя, использующие репродуктивные методы обучения и считающие, что школьники у них на уроке работают активно, – заблуждаются. Это – мнимая активность, не приводящая к устойчивой системе знаний, умений и навыков.

Репродуктивные методы обучения тоже предполагают некоторую самостоятельность в учебном процессе, но эта самостоятельность ограничивается лишь этапами закрепления и контроля. На этапах актуализации и формирования новых знаний, умений и навыков обучающиеся следует исключительно инструкциям учителя, а всякая самостоятельность рассматривается нередко как нежелательная самодеятельность и пресекается.

Репродуктивные методы не способствуют вовлеченности обучающихся в учебный процесс или, если и способствуют, то только на основе внешней мотивации (вынуждения, принуждения, приказов, уговоров и пр.). Такая вовлеченность неустойчивая и непродуктивная. Истинная вовлеченность обучающегося в процесс познания наблюдается тогда, когда обучающийся приходит к этим знаниям самостоятельно. Проблемные методы, в отличие от репродуктивных, опираются на познавательную активность обучающихся.

Развитие обучающихся с помощью проблемных методов осуществления целостного образовательного процесса происходит по всем аспектам: познавательным, речевым, интеллектуальным. Продуктивность проблемных методов обучения оценивается именно по тому, сколько аспектов развития охватывают данные методы на данном этапе решения образовательных задач.

Проблемные методы обучения – это активные способы формирования знаний, умений, навыков. Обучающиеся включаются в учебно-познавательную деятельность очень активно, с желанием достичь нужных результатов. При этом нацеленность на результат носит не внешнюю, а внутреннюю обусловленность. Обучающийся желает добыть знания, потому что ему это интересно, а не потому, что это надо учителю, родителям. Именно поэтому проблемные методы обучения целесообразно применять на всех этапах образовательного процесса.

Также проблемные методы обучения предполагают постепенный отказ от репродуктивных методов, доказавших малую эффективность в процессах формирования необходимых компетенций. Если продуктивность метода связана с поиском новых знаний, то учебная задача оформляется в виде проблемы, которую необходимо разрешить. Однако велика роль проблемных методов на стадии закрепления материала. Продуктивное закрепление знаний, умения или навыка – это процесс, связанный с усилением регулятивных компетенций обучающихся (навыков самоконтроля, самооценки и т.д.).

Среди проблемных методов решения стереометрических задач следует выделить: диалоговый, эвристический и поисковый.

Диалогический метод – это обусловленная принципами обучения система регулятивных правил подготовки учебного материала и проведения сообщающей беседы с целью объяснения учебного материала учителем, усвоения его учащимися; побуждения учащихся к участию в постановке проблем и их решении; активизации их учебной деятельности. Работа диалогическим методом осуществляется в форме беседы на уроках первого и третьего типа (изучения нового материала; обобщения и систематизации знаний). В беседе преподаватель привлекает учащихся к ответам на такие вопросы, которые обращены к имеющимся у них знаниям и умениям. Доля их самостоятельности в учебной деятельности определяется количеством вопросов репродуктивного характера. При постановке вопросов, требующих для ответа новой информации, новых знаний, новых подходов, преподаватель либо сам отвечает на них, либо организует изучение учащимися учебного пособия, видеофильма и пр. Этот метод очень динамичен, он может перейти и в эвристический, и при необходимости в монологический, может применяться практически на любом этапе урока.

Эвристический метод – это обусловленная принципами обучения система регулятивных правил подготовки учебного материала и проведения эвристической беседы с решением познавательных задач. Применяется эвристический метод при изучении нового материала, имеющего противоречивый характер, или при совершенствовании ранее усвоенных знаний с целью обобщения полученных ранее впечатлений, стимулирования многоаспектного осмысления явлений, самостоятельного поиска учащимися новых способов деятельности, которым их ранее не обучали. В большой степени применение этого метода зависит от уровня обученности и развития учащихся, особенно от сформированности их познавательных умений. Эвристический метод применяется в форме эвристической беседы во время семинара, дискуссии, учебной конференции. Учитель сочетает частичное объяснение нового с постановкой проблемных заданий. Учащиеся выполняют самостоятельные работы поискового типа: анализируют проблемные ситуации, ставят проблемы и решают их, находят новые знания и способы действий.

Поисковый метод – это обусловленная принципами обучения система регулятивных правил подготовки учебного материала и организации преподавателем самостоятельной работы учащихся по решению проблемных заданий с целью усвоения ими новых понятий и способов действий и развития у них интеллектуальной и других сфер. Поисковый метод (как более сложный) применяется реже эвристического на доступном учащимся материале, изучение которого чаще связано с выполнением практических или теоретических работ поискового характера.

 

2.9 Разработка урока по решению стереометрических задач

В рамках данного исследования разработан урок в 11 классе по теме «Решение стереометрических задач по прямому круглому конусу».

Цель урока – формирование знаний о конусе в процессе решения стереометрических задач.

Задачи урока:

1) обучающие – формирование предметных компетенций, а именно:

– формирование знаний о конусе как о фигуре вращения, о его развертке;

– формирование знаний об основных конструктивных элементах конуса;

– формирование умения находить площадь полной поверхности прямого круглого конуса;

2) воспитательные: формирование личностных универсальных действий;

3) развивающие – формирование метапредметных компетенций (познавательных, регулятивных и коммуникативных).

Форма организации работы на уроке: индивидуальная, парная.

Содержание урока – решение стереометрических задач.

Методы: проблемные (диалогические и поисковые).

Средства: учебник, компьютер, интерактивная доска.

Конспект урока.

1. Организационный этап. На организационном этапе учитель устанавливает атмосферу урока, готовит обучающихся к восприятию нового материала.
2. Актуализирующий этап. На экране изображен прямой круглый конус (рис. 1).

Рисунок 1 – Актуализирующий рисунок к уроку

Учитель предлагает проблемную ситуацию.

Проблемная ситуация: нужно понять, что является разверткой прямого круглого конуса. Обучающимся предлагается воспользоваться листом бумаги формата А4, из которого вырезан треугольник. Работа осуществляется в парах. Работая с листом, обучающиеся приходят к выводу о том, что треугольник конструктивно не может быть разверткой конуса, а также к выводу о том, что разверткой конуса служит сектор (рис. 2).

Рисунок 2 – Рисунок, полученный обучающимися в ходе разрешения проблемной ситуации

3. Основной этап.

3.1. Обучающиеся знакомятся с конструктивными элементами конуса: боковой поверхностью, основанием и его радиусом (R), образующей (L), высотой (H).

3.2. Решение задач.

3.2.1. Проблемная задача о нахождении образующей прямого круглого конуса.

Высота прямого круглого конуса равна H, радиус основания прямого круглого конуса равен R. Найти образующую L прямого круглого конуса.

Обучающиеся записывают условие и вопрос задачи.

Речь учителя: что нужно рассмотреть для решения данной задачи?

Ответы обучающихся: прямоугольный треугольник, образованный высотой, радиусом основания и образующей.

Обучающиеся делают рисунок (рис. 3).

Рисунок 3 – Рисунок к задаче 3.2.1

Речь учителя: какой теоремой воспользуемся?

Ответы обучающихся: теоремой Пифагора.

Решая задачу, обучающиеся самостоятельно приходят к выводу о том, что образующая прямого круглого конуса L = .

3.2.2. Проблемная задача о нахождении площади полной поверхности прямого круглого конуса.

Высота прямого круглого конуса равна H, радиус основания прямого круглого конуса равен R, образующая прямого круглого конуса равна L. Найти площадь полной поверхности Sпп прямого круглого конуса.

Обучающиеся записывают условие и вопрос задачи.

Речь учителя: из чего будет складываться площадь полной поверхности прямого круглого конуса?

Ответы обучающихся: из площади боковой поверхности и площади основания.

Речь учителя: что нужно знать для вычисления площади боковой поверхности?

Ответы обучающихся: длину окружности основания.

Обучающиеся делают рисунок (рис. 4).

Рисунок 4 – Рисунок к задаче 3.2.2

Работая в парах, обучающиеся находят, что площадь боковой поверхности прямого круглого конуса Sбп = = = πRL.

Речь учителя: что представляет собой площадь основания прямого круглого конуса?

Ответы обучающихся: это площадь круга радиуса R.

Работая в парах, обучающиеся находят, что площадь полной поверхности прямого круглого конуса Sпп = πRL + πR2 = πR(L + R).

В конечном результате обучающиеся записывают формулу площади полной поверхности прямого круглого конуса, которая связывает только высоту и радиус основания: Sпп = πR( + R).

4. Закрепляющий этап.

Учитель предлагает обучающимся несколько задач для самостоятельного решения.

А. Площадь полной поверхности прямого круглого конуса равна 100 см2, а высота прямого круглого конуса вдвое больше радиуса его основания. Найти образующую прямого круглого конуса.

Б. Образующая прямого круглого конуса образует с его основанием угол, равный 600. Площадь основания прямого круглого конуса равна 40 м2. Найти площадь боковой поверхности прямого круглого конуса.

В. Высота прямого круглого конуса втрое больше радиуса его основания. Найти отношение площади полной поверхности прямого круглого конуса к площади его боковой поверхности.

 

Выводы по второй главе

1. Методика решения планиметрических и стереометрических задач должна основываться на проблемно-развивающем подходе к обучению, когда обучающиеся не решают задачу по определенному алгоритму, а приходят самостоятельно к необходимым выводам, которые помогут им в успешном решении.
2. Проблемные методы решения задач должны быть поисковыми и диалогическими. Только сочетание этих методов позволит достичь главной цели урока. Кроме того, такое сочетание методов обеспечивает сформированность необходимых навыков.

 

ЗАКЛЮЧЕНИЕ

Новая концепция профильного обучения на старшей ступени общего образования предоставила учащимся широкие возможности самостоятельного выбора не только уровня, но и направления математической подготовки, поставив и перед теорией, и перед практикой обучения математике задачу создания системы курсов, позволяющих выстраивать индивидуальные образовательные траектории для учащихся

Чем богаче и разностороннее мир ребенка, тем большее количество таких первоначальных знаний он получает до начала обучения в школе. По наблюдениям многих учителей и специалистов-психологов при неверном обучении ранняя способность оперировать геометрическими образами и синтезировать геометрические знания может в дальнейшем не только не развиваться, но даже резко ослабевать.

Одной из главных задач преподавания геометрии является задача планомерного, систематического развития геометрического, образного мышления, восприятие геометрии не только как школьного предмета, но и как феномена человеческой культуры.

В процессе решения задач по геометрии учитель может эффективно формировать элементы алгоритмической культуры школьников. Задачи развивают поисковые навыки решения практических проблем, приобщают к посильным самостоятельным исследованиям, что очень важно в формировании умений и навыков умственного труда.

Посредством задач, даже простейших из них, более глубоко осознаются теоретические сведения об основных геометрических фигурах, так как в процессе решения этих задач ученик создает наглядную модель изучаемых свойств и отношений и работает с этой моделью. Решение  планиметрических задач развивает такие качества личности, как внимание, настойчивость и целеустремленность, инициативу, изобретательность, дисциплинированность, трудолюбие.

В исследовании проанализированы наиболее эффективные методы решения стереометрических задач в школьном курсе геометрии.

К таким методам относятся методы проблемно-развивающего обучения. При реализации таких методов учитель выступает в качестве наставника, под руководством которого осуществляется решение, он не дает готовых алгоритмов и формул.

Для обоснования эффективности проблемных методов решения стереометрических задач были выявлены проблемные методы решения таких задач, проанализированы различные подходы к методологии их решения. Стереометрические задачи решаются путем подключения целостного математического мышления, которое обязательно включает пространственные мыслительные процессы. Кроме того, решение стереометрических задач предполагает развитие мыслительной деятельности в целом. Поэтому актуален проблемно-развивающий подход.

При таком подходе к решению стереометрических задач обучающиеся самостоятельно выводят формулы, формируют рисунки к задаче, создают опоры. Учитель может задавать проблемные вопросы – и тогда проблемное обучение становится диалоговым. Однако не следует превращать весь урок по решению стереометрических задач в диалог; необходимо также использовать поисковые методы.

Список использованной литературы

 

1. Ананченко, К.О. Общая методика преподавания математики в школе / К.О. Ананченко. – Мн: Университет, 1997. – 225 с.
2. Глейзер, Г.Д. Развитие пространственных представлений школьников при изучении геометрии / Г.Д. Глейзер. – М.: Педагогика, 1972.
3. Гусев, В.А. Методика преподавания геометрии в школе / В.А. Гусев [и др.]. – М.: Академия, 2004. – 368 с.
4. Гусев, В.А. Психолого-педагогические основы обучения математике / В.А. Гусев. – М.: Вербум-М, Академия, 2013. – 343 с.
5. Давыдов, В.В. Проблемы развивающих обучений. Опыт теоретического и экспериментального психологического исследования / В.В. Давыдов. – 4-е изд., перераб. – М.: Педагогика, 2016. – 240 с.
6. Епишева, О.Б. Учить школьников учиться математике / О.Б. Епишева. – М.: Просвещение, 2011. – 127 с.
7. Истратий, А.В. Возможности использования программ трехмерного моделирования при изучении стереометрии в основной школе / А.В. Истратий // Вестник науки и образования. – Т. 3. – 2018.
8. Клековкин, Г.А. Роль и место фузионизма в школьном геометрическом образовании / Г.А. Клековкин // Образование и наука. – 2012. – № 3. – С. 77-92.
9. Колягин, Ю.М. Методика преподавания математики в старшей школе / Ю.М. Колягин. – М.: Просвещение, 2009. – 336 с.
10. Левитас, Г.Г. Фузионизм в школьной геометрии / Г.Г. Левитас // Математика в школе. – 1995. – № 6.
11. Метельский, Н.В. Дидактика математики / Н.В. Метельский. – Мн.: Изд-во БГУ, 2012. – 254 с.
12. Методика преподавания математики в старшей школе: Общая методика / В.А. Оганесян, Ю.М. Колягин, В.Я. Саннинский, Г.Л. Луканкин. – М.: Просвещение, 2010. – 386 с.
13. Методика преподавания геометрии в старших классах средней школы / Под ред. А.И. Фетисова. – М.: Просвещение, 1967.
14. Прояева, И.В. Об особенностях преподавания отдельных вопросов стереометрии в школьном курсе геометрии / И.В. Прояева, А.Д. Сафарова // Мир науки, культуры, образования. – 2017. – № 2 (63). – С. 53-55.
15. Санина, Е.И. Обобщающее повторение начал стереометрии / Е.И. Санина // Математика в школе. – 1993. – № 6. – С. 12-14.
16. Смирнова, И.М. Компьютер помогает геометрии / И.М. Смирнова. – 2-е изд. – М.: Дрофа, 2009.
17. Смирнова, И.М. Методика преподавания геометрии в школе / И.М. Смирнова. – М.: Просвещение, 2017. – 266 с.
18. Смирнова, И.М. Реализация метапредметного подхода в обучении геометрии / И.М. Смирнова // Вестник МГОУ. – 2018. – № 2. – С. 94-99.
19. Старшинова, А.В. Изучение различных видов проекций фигур как средства их изображения учащимися средней школы / А.В. Старшинова: Дисс. … канд. пед. наук. – М., 2005.
20. Столяр, А.А. Методы обучения математике / А.А. Столяр. – Мн.: Высшая школа, 2011. – 191 с.
21. Тихомиров, В.М. Геометрия в современной математике и математическом образовании / В.М. Тихомиров // Математика в школе. – 1993. – № 4.
22. Фридман, Л.М. Теоретические основы методики обучения математике: Пособие для учителей, методистов педагогических высших учебных заведений / Л.М. Фридман. – М.: Флинта, 2012. – 224 с.
23. Хазанкин, Р.Г. Десять заповедей учителя математики / Р.Г. Хазанкин // Народное образование. – 1991. – № 1.
24. Хазанкин, Р.Г. Как увлечь учеников математикой / Р.Г. Хазанкин // Народное образование. – 1987. – № 10.
25. Weyl, H. Mathematisches denken. – B., 2015.
26.      https://multiurok.ru/
27. https://oge.sdamgia.ru/

https://infourok.ru/

---

1 2