Страница: 1 2
Содержание
- Введение
- Глава 1.1. «Зарождение и развитие теории портфельного инвестирования»
- Глава 1.2. «Математические модели портфельных решений»
- Глава 2.1. Модели прогнозирования финансовых временных рядов в условиях гипотезы эффективного рынка
- Глава 2.2. Адаптивные модели прогнозирования финансовых временных рядов в условиях гипотезы фрактального рынка
- Глава 3.1. Формирование портфелей с условно средней доходностью
- Глава 3.2. Оптимальные портфели в условиях гипотезы фрактального рынка
- Заключение
- Список литературы
Введение
В рыночной системе ведения хозяйства доминируют принципиально новые и не совсем освоенные нашей экономикой механизмы привлечения финансовых средств, направляемых на поддержание и развитие инвестиционных процессов. Эти новые механизмы основаны на рыночной модели инвестирования. Они способствуют сокращению централизованных вложений и привлекают частные инвестиции, ограничивая тем самым деятельность государства в качестве непосредственного инвестора. Создается ситуация, когда решающее значение придается росту объема и эффективности негосударственных инвестиций, основными источниками которых должны стать собственные средства предприятий и привлеченные источники, прежде всего средства банков, институциональных инвесторов и населения.
Неразвитость банковской системы России и ее неспособность предоставить свои избыточные ресурсы производственному сектору экономики ставят вопрос об ускоренном развитии рынка ценных бумаг в число стратегически важных направлений развития экономики в целом. По сути, рынок является самым эффективным экономическим регулятором. Он способствуют привлечению инвестиций на предприятия и доступ последних к более дешевому (по сравнению с банковскими кредитами) капиталу. С его помощью инвестиции автоматически направляются в наиболее эффективные отрасли хозяйственной деятельности и жизнеспособные бизнес-структуры. Как механизм трансформации сбережений в инвестиции он является сегодня той сферой, в которой формируются основные финансовые источники экономического роста, концентрируются и распределяются необходимые экономике инвестиционные ресурсы.
Эффективное функционирование рынка ценных бумаг предполагает наличие ряда обязательных условий, среди которых важное место занимает инвестиционная теория, на основе которой принимаются конкретные инвестиционные решения. Ключевой в данной теории является проблема анализа и формирования портфеля ценных бумаг.
Начало исследований в области обоснования инвестиционных решений было положено Г. Марковицем в 1952 году. В настоящее время изучение этой проблемы продолжается. Основной вклад, по вполне очевидным причинам, в развитие теории портфеля ценных бумаг внесли ученые стран Запада и США. Прежде всего, это классики данной теории: Д. Вильяме, Дж. Линтнер, Г. Марковиц, Дж. Моссин, М. Миллер, Ф. Модельяни, Р. Ролл, С. Росс, Дж. Тобин, Ф. Блэк, М. Шоулс, Дж. Кокс, М. Рубинштейн, У. Шарп, Б. Фишер, И. Фишер и др. Благодаря их усилиям была построена стройная теория эффективного рынка, многие аспекты которой успешно применяются при обосновании практических решений.
Становление российского рынка ценных бумаг стимулировало исследования отечественных ученых, направленных на дальнейшее развитие теории инвестирования. Интересные результаты были получены в работах М.Ю. Алексеева, Л.О. Бабешко, А.Н. Буренина, И.В. Волошина, А.П. Иванова, Ю.Ф. Касимова, М.А. Кудрявцева, Ю.П. Лукашина, Я.М. Миркина, И.А. На-талухи, И.Г. Наталухи, А.О. Недосекина, Е.М. Четыркина, А.С. Шведова, А.Н. Ширяева, Л.П. Яновского и др. Их исследования имеют большое теоретическое и практическое значение для развития инвестиционной теории, адаптированной к российской действительности.
Вместе с тем, несмотря на значительное количество работ по теории портфеля ценных бумаг и активное практическое использование отдельных рекомендаций этой теории, процесс ее создания далеко не завершен. Продолжается поиск причин, которые не позволяют непосредственно использовать в практическом финансовом менеджменте результаты оптимального моделирования портфельных решений. Критические взгляды на модель формирования оптимальных портфелей оставляли без должного внимания вопрос отсутствия взаимосвязи между данными, используемыми для формирования количественных характеристик портфеля, и периодом, в течение которого, как ожидает инвестор, портфель должен приносить доход.
В данной работе заостряется внимание именно на этом моменте и реализуется идея построения портфелей с условно ожидаемой доходностью, структура которых ориентирована на динамику доходности упреждающего периода.
Объектом исследования является портфель ценных бумаг.
Предмет исследования — математический аппарат формирования портфеля ценных бумаг.
Целью работы является анализ математического аппарата формирования оптимального портфеля ценных бумаг.
Для достижения этой цели в дипломной работе поставлены следующие задачи:
- рассмотрение зарождения и развития теории портфельного инвестирования;
- изучение основных подходов к формированию портфеля ценных бумаг;
- анализ методики формирования портфеля с условно ожидаемой доходностью;
- рассмотрение моделей прогнозирования доходностей с локально действующим многошаговым адаптивным механизмом;
- анализ методики портфельного инвестирования, которую целесообразно применять в условиях гипотезы фрактального рынка;
- рассмотрение схемы оценки эффективности портфельных инвестиционных стратегий на основе поступреждающего тестирования;
- верификация проанализированных моделей и методик.
Теоретическую и методологическую основу дипломной работы составили труды отечественных и зарубежных ученых по вопросам анализа рынка ценных бумаг, инвестиционного менеджмента, эконометрического моделирования и адаптивного прогнозирования финансовых процессов.
Информационно-эмпирическую базу исследования составили архивы котировок акций, размещенные на сайтах Российской торговой системы (www.rts.ru) и РИА «РосБизнесКонсалтинг» (www.rbk.ru).
Структура работы обусловлена предметом, целью и задачами дипломного проекта. Работа состоит из введения, трех глав, заключения и списка использованной литературы.
Во введении обоснована актуальность темы дипломной работы, определены предмет и объект исследования, сформулирована цель и поставлены задачи, решение которых необходимо для ее достижения.
В первой главе рассматривается история развития и современное состояние теории портфельных решений, ставшей основой современного подхода к управлению риском. Приводится достаточно полное описание математических моделей, применяемых в теории и практике инвестирования.
Во второй главе исследуются возможности прогнозирования доходности финансовых активов с целью использования получаемых прогнозных оценок в задачах оптимизации портфельных решений. Для ситуаций, когда выполняются предположения гипотезы эффективного рынка, рассматривается процедура формирования производных временных рядов с памятью, обеспечивающих получение прогнозных оценок усредненной доходности, на основе которых строятся портфели с условно ожидаемой доходностью. Для случаев, когда доминируют предположения гипотезы фрактального рынка, прогноз осуществляется по специально разработанной модели с локально действующим многошаговым адаптивным механизмом.
В третьей главе представлены методики формирования инвестиционных портфелей, ориентированных на инвесторов с идентичным поведением и инвесторов с различными горизонтами инвестирования. Методики иллюстрируются полномасштабными расчетами, включающими все этапы формирования портфелей.
В заключении изложены основные результаты и выводы по дипломной работе.
Глава 1.1. «Зарождение и развитие теории портфельного инвестирования»
Во второй половине двадцатого столетия в механизмах регулирования экономики промышленно развитых стран произошли радикальные изменения. Отдельные изолированные региональные финансовые рынки стали функционировать как единый международный финансовый рынок. Информатизация, объединение рынков на основе компьютерных сетей с использованием новейших информационных технологий пришли на смену традиционной фондовой бирже с ее торговыми залами и торговлей «с голоса». Начало этого периода ознаменовалось еще одним событием, которое не сразу было оценено.
В июне 1952 года в ведущем академическом журнале по финансовым вопросам «Journal of Finance» была опубликована статья Гарри Марковича под названием «Выбор портфеля». В этой статье впервые была предложена математическая модель формирования оптимального портфеля ценных бумаг и были приведены методы построения таких портфелей при определенных условиях.
Сам термин «портфель» («portfolio») понимался как «набор бумаг, фиксирующих имущественные права». Портфель в результате решения задачи Марковича наделялся структурой, благодаря которой он принципиально отличался от пакетов акций отдельных компаний, рассматриваемых изолированно.
Основной заслугой работы Марковица явилась предложенная теоретико-вероятностная формализация понятия доходности и риска. Это сразу позволило перевести задачу выбора оптимальной инвестиционной стратегии на строгий математический язык.
С вычислительной точки зрения получающаяся оптимизационная задача относится к классу задач квадратичной оптимизации при линейных ограничениях. К настоящему времени вместе с задачами линейного программирования это один из наиболее изученных классов оптимизационных задач, для которых разработано большое число достаточно эффективных алгоритмов.
Марковиц постоянно занимался усовершенствованием и развитием предложенной модели. В 1959 г. выходит первая монография, посвященная изложению предложенного подхода. В 1991 г. выходит книга, подводящая итог почти сорокалетнему периоду работы по теории выбора инвестиционного портфеля.
Первая работа Марковича не привлекла особого внимания, по крайней мере, со стороны теоретиков-экономистов и практиков. Для 50-х гг. прошлого века применение теории вероятностей к финансовой теории было само по себе новым делом. К тому же ограниченность в использовании вычислительной техники и сложность предложенных Марковицем алгоритмов не позволили осуществить реализацию его идей на практике.
В 1963 г. учеником Марковича Уильямом Шарпом была предложена так называемая однофакторная модель рынка капиталов, в которой впервые появились, ставшие знаменитыми впоследствии, «альфа»- и «бета»- характеристики акций. На основе однофакторной модели Шарп предложил упрощенный метод выбора оптимального портфеля, который за счет дополнительных предположений сводил задачу квадратичной оптимизации к линейной. В некоторых случаях, для небольших размерностей, эта задача могла быть решена практически «вручную». Такое упрощение создало возможность применения методов портфельной оптимизации на практике.
Кризис финансовых рынков в начале семидесятых и пересмотр, в связи с этим, принципов инвестирования, развитие вычислительной техники, а также совершенствование методик оценивания показателей «альфа» и «бета» отдельных ценных бумаг и индекса доходности рынка в целом привело к появлению первых пакетов программ для решения задач управления портфелем ценных бумаг.
В практике современного финансового менеджмента модель Марковица используется в основном на первом этапе формирования портфеля активов при распределении инвестируемого капитала по различным типам активов: акциям, облигациям, недвижимости и т. д. Однофакторная модель Шарпа используется на втором этапе, когда капитал, инвестируемый в определенный сегмент рынка активов, распределяется между отдельными конкретными активами, составляющими выбранный сегмент (т. е. по конкретным акциям, облигациям и т. д.).
Расширение влияния идей Марковица на финансовую теорию стало более заметным после появления в конце 50-х и начале 60-х гг. прошлого века работ Джеймса Тобина. Между подходами Марковица и Тобина есть существенные различия. Основные идеи подхода Марковица лежат в русле микроэкономического анализа, поскольку он акцентирует внимание на поведении отдельного инвестора, формирующего оптимальный, с его точки зрения, портфель на основе собственной оценки доходности и риска выбираемых активов. К тому же первоначально модель Марковица касалась в основном портфеля акций, т.е. активов, которые принято считать рискованными. В своей модели Тобин предложил включить в анализ безрисковые активы, в качестве которых чаще всего рассматриваются государственные облигации. Подход Тобина является, по существу, макроэкономическим, поскольку основным объектом его изучения является распределение совокупного капитала в экономике по двум его формам: наличной (денежной) и не наличной (в виде ценных бумаг).
Корректность моделей, используемых для формирования оптимальных портфелей, оценивается по тому, насколько в них находят отражение основные положения доминирующей гипотезы. Большинство моделей, как правило, являются корректными, однако результаты их практического использования не оправдывают ожиданий инвесторов.
Основная гипотеза финансового рынка формировалась одновременно с созданием математических моделей, о правдоподобности которых имело смысл говорить только при выполнении определенных предположений. Став основой современной финансовой теории, эти модели автоматически интегрировали предположения, гарантирующие их правдоподобность, в гипотезу доминирующую сейчас, как в теории, так и в практике современного финансового анализа. Эту гипотезу принято называть гипотезой эффективного рынка.
Ключевой концепцией, лежащей в основе понятия эффективного рынка, является предположение о том, что цены мгновенно ассимилируют новую информацию и устанавливаются таким образом, что арбитражные возможности исключаются.
Выделяют три формы эффективности рынка.
- Слабая форма эффективности рынка. Текущие цены отражают всю информацию, заключенную в прошлых ценах.
- Полустрогая форма эффективности рынка. Текущие цены отражают всю публичную информацию.
- Строгая форма эффективности рынка. Текущие цены отражают всю информацию, в том числе частную и инсайдерскую.
Традиционно под эффективным рынком понимают вторую форму эффективности. При этом делаются следующие предположения:
- Активы на финансовом рынке оцениваются в рамках какой-либо модели ценообразования (САРМ, АРТ).
- Цены на финансовые активы реагируют на новую информацию мгновенно и точно.
- Инвесторы одинаково интерпретируют имеющуюся у них одну и ту же информацию для прогноза доходностей активов. Поэтому ошибки в прогнозах, а следовательно, возникновение экономической прибыли или убытка, не предсказуемы на основе имеющейся на момент прогноза информации.
Кстати, отсюда также следует, что инвесторы не могут на рынке постоянно получать экономическую прибыль.
В заключении отмечу еще один недостаток модели Марковича, который стал основной преградой на пути практического ее использования. Модель строится без учета динамики рынка. Неявно предполагается, что свои
оптимальные свойства, определенные в текущий момент времени, она сохранит и в перспективном периоде. Это предположение полностью согласуется с гипотезой эффективного рынка, в соответствии с которой лучшим прогнозом для цены финансового актива является его текущая цена.
Реальность не подтверждает справедливость этого вывода, что не сложно продемонстрировать результатами эмпирических исследований.
Вычислительный эксперимент проводился на примере формирования портфеля из активов шести компаний: Газпром, Лукойл, Сбербанк, Ростелеком, Уралкалий и Норникель. В качестве исходных данных использовались котировки акций этих компаний за период с 01.12.11 по 30.11.12. Методика проведения сравнительного анализа эффективности портфелей предусматривает деление всей выборочной совокупности данных на две подвыборки. В первую подвыборку были включены данные за первые семь месяцев, а во вторую — за оставшиеся пять. Смысл этой методики в том, что по данным первых семи месяцев строился оптимальный портфель, а затем рассматриваются его характеристики на данных пяти месяцев второй подвыборки, которую целесообразно называть поступреждающим периодом. Затем строился оптимальный портфель на данных второй подвыборки, которые для этого портфеля уже не интерпретируются как поступреждающие. Характеристики второго портфеля сравниваются с характеристиками первого портфеля.
Сравнение результатов, приведенных в таблице 1.1, позволяет сделать однозначный вывод: портфель оптимальный в текущий момент времени теряет свои оптимальные свойства в перспективном периоде. В модели Марко-вица не предусмотрены свойства, которые могли бы гарантировать ее устойчивость при любых изменениях в структуре стоимости акций. Если в качестве исходных данных для построения портфеля использовать прогнозные оценки, то портфель в меньшей степени теряет свои оптимальные свойства.
Таблица 1.1 Сравнительный анализ эффективности портфелей
| Компании | Исторический период | Поступреждающий период | |||
| Средние значения доходности | Портфель I | Средние значения доходности | Портфель I | Портфель II | |
| Газпром | -0,0722 | -0,8900 | -0,0794 | -0,8900 | -7,6453 |
| Лукойл | 0,0571 | 2,3423 | 0,1886 | 2,3423 | 16,2498 |
| Сбербанк | 0,0192 | 1,6999 | 0,0478 | 1,6999 | -0,5340 |
| Ростелеком | -0,1918 | -11,6855 | 0,0447 | -11,6855 | 1,0821 |
| У рал кал и и | 0,0533 | 10,1804 | -0,0065 | 10,1804 | -2,0639 |
| Норникель Показатели | 0,0310 | -0,6472 | -0,1055 | -0,6472 | -6,0886 |
| Показатели | |||||
| Доходность | 2,9944 | 0,0732 | 4,3514 | ||
| Риск | 0,7610 | 0,8319 | 1,6541 | ||
| Риск/Доходность | 0,2541 | 11,3714 | 0,3801 | ||
К середине 60-х гг. XX века заканчивается первый этап развития современной теории инвестиций в том виде, который придали ей Марковиц и Тобин. С 1964 г. появляются три работы, открывшие следующий этап в инвестиционной теории, связанный с так называемой моделью оценки капитальных активов, или САРМ (Capital Asset Price Model). Работы Шарпа, Линтне-ра, Моссина были посвящены, по существу, одному и тому же вопросу: что все инвесторы, обладая одной и той же информацией, одинаково оценивают доходность и риск отдельных акций. Предположения лежащие в основе гипотезы эффективного рынка остаются по сути теми же самыми. Допускается только то, что все инвесторы формируют свои оптимальные в смысле теории Марковича портфели акций исходя из индивидуальной склонности к риску. Интерес представляет вопрос о том, как в этом случае сложатся цены на рынке акций? Таким образом, на САРМ можно смотреть как на макроэкономическое обобщение теории Марковица. Основным результатом САРМ явилось установление соотношения между доходностью и риском актива для равновесного рынка. При этом важным оказывается тот факт, что при выборе оптимального портфеля инвестор должен учитывать не весь риск, связанный с активом (риск по Марковицу), а только часть его, называемую систематическим, или недиверсифицируемым риском.
Эта часть риска актива тесно связана с общим риском рынка в целом и количественно представляется коэффициентом β (бета), введенным Шарпом в его однофакторной модели. Остальная часть (так называемый несистематический, или диверсифицируемый риск) устраняется выбором соответствующего (оптимального) портфеля. Характер связи между доходностью и риском имеет вид линейной зависимости, и тем самым обычное практическое правило «большая доходность значит большой риск» получает точное аналитическое представление. Свойства САРМ позволяет при известных значениях {βi} все акции разделить на четыре группы:
- βi = 1. Если выполняется это равенство, то ожидаемая доходность акции находится на уровне средней рыночной доходности.
- 0 < βi < 1. В этом случае акции обладают меньшим риском, но при этом получаются менее доходными. Акции, принадлежащие к подобной группе, называются оборонительными.
- βi > 1. То есть по акциям ожидается доходность выше средней, но этому сопутствует больший риск. Акции, принадлежащие к этой группе, называются агрессивными.
- βi = 0. В этом случае мы имеем дело с безрисковым активом.
Данный сравнительный анализ популярен в среде инвестиционных аналитиков и используется при осуществлении активных стратегий инвестиционного менеджмента.
Все последующее десятилетие до 1976 г. развитие финансовой теории шло под доминирующим влиянием САРМ. В 1977 г. эта теория подверглась жесткой критике в работах Р. Ролла. На интуитивном уровне эта критика состоит в том, что рыночный портфель включает в себя фиксированный набор рисковых активов, тогда как набор акций, включаемых в биржевой индекс, меняется с течением времени. К тому же, в отличие от рыночного портфеля, весовые коэффициенты в биржевом индексе могут иметь ограничения сверху, а сами индексы могут включать дивиденды. Есть и формальное доказательство точки зрения Ролла. Оно основано на проверке гипотезы H0: α = 0. Мнение Ролла, основанное на приведенных рассуждениях, состоит в том, что САРМ следует отвергнуть, поскольку она в принципе не допускает эмпирической проверки. Вопрос о принципиальной верифицируемости САРМ вызывает горячие споры и по сей день.
Примерно в это же время С. Россом была предложена альтернативная модель оценки капитальных активов АРТ (Arbitrage Pricing Theory — арбитражная теория оценивания) получившая название «арбитражной модели». Эта модель строится на основе принципа, состоящего в том, что соотношение между ожидаемой доходностью и риском должно быть таким, чтобы ни один индивидуальный инвестор не мог получить неограниченный доход от чисто арбитражной сделки. Этот принцип невозможности арбитража можно сформулировать в «физических терминах» как невозможность создать «финансовый вечный двигатель», т.е. машину без всякого риска, неограниченно долго «вытягивающей» деньги с рынка. Адепты арбитражной теории, в частности, Росс и Ролл утверждают, что эта теория допускает, по крайней мере, эмпирическую проверку. Были предложены конкретные модели .
Модель Чена — Ролла — Росса. В этой модели использовались следующие факторы, характеризующие доходность финансовых активов:
- разница в долгосрочной и краткосрочной ставках процента, используемая для идентификации делового цикла в экономике;
- разница в ставках процента для облигаций с высоким и низким рейтингами, используемые для отражения совокупного уровня риска в экономике;
- изменения в промышленном производстве;
- изменения уровня инфляции.
Модель Фамы — Френча. С помощью этой модели рассчитываются доходности как рисковых (акции), так и безрисковых активов (облигаций). В модель были включены следующие факторы:
- разница в доходности портфелей акций крупных и мелких компаний;
- разница в доходности портфелей акций с высоким и низким значениями показателя, представляющего отношение бухгалтерской стоимости акций к рыночной стоимости тех же самых акций;
- разница в месячной доходности портфелей долгосрочных государственных облигаций и месячных казначейских обязательств;
- разница в месячной доходности портфелей долгосрочных корпоративных и государственных облигаций.
Недостатков у этих моделей много и они очевидны. Прежде всего, это неоднозначность, как в идентификации самих факторов, так и в определении их количества. Кроме того модели не обладают достаточной универсальностью. Выводы, сделанные с их помощью относительно одной группы активов, могут оказаться неверными для другой. Поэтому модели АРТ так и не стали инструментом практических расчетов.
САРМ остается, пожалуй, самой значительной и влиятельной современной финансовой теорией. Практические руководства по финансовому менеджменту в части выбора стратегии долгосрочного инвестирования и по сей день основываются исключительно на САРМ. В целом к настоящему времени инвестиционная теория, синтезирующая портфельную теорию Марковича — Тобина и САРМ, получает широкое применение. В 1981 г. получает Нобелевскую премию Дж. Тобин, а в 1990 г. премия присуждается Марковичу и Шарпу совместно с Мертоном Миллером.
Несмотря на успешное использование САРМ в практике обоснования инвестиционных решений, эта модель в большей степени является позитивной, чем нормативной. С ее помощью удается понять механизм, обеспечивающий более высокую доходность акций по сравнению с безрисковыми ценными бумагами, но барьер между реальностью и неопределенностью будущего так и остается не преодолимым. Гипотеза эффективного рынка гарантирует надежность инвестиционных стратегий, выстроенных в соответствии с САРМ. Однако, как известно, реальность рынка часто заставляет инвесторов корректировать эти стратегии. Никто и не отрицает, что с течением времени значения бета коэффициентов изменяются. Не случайно Нью-Йоркская фондовая биржа периодически публикует бета коэффициенты специально для инвесторов.
Введенное при разработке выше рассмотренных моделей понятие «риск», предупреждая о возможных потерях, ориентировало на разработку стратегий, обеспечивающих надежную защиту от риска. Обязательным элементом таких стратегий стали опционы и различные их разновидности. Можно было рисковать или покупать защиту от риска. Но сколько должна стоить такая защита?
Попытка ответить на этот вопрос связана с циклом исследований, в основу которых положена гипотеза эффективного рынка. Гипотеза эффективного рынка и связанная с ней модель «случайного блуждания» рыночных цен активов стимулировали применение динамических теоретико-вероятностных моделей, основанных на теории случайных процессов. В русле этих идей в 1973 г. М. Шоулсом и Ф. Блэком была предложена модель опционов, получившая название модели Блэка — Шоулса. Эта модель основывалась на возможности осуществления безрисковой сделки с одновременным использованием акции и выписанным на нее опционом. Стоимость такой сделки должна совпадать со стоимость безрисковых активов на рынке, а поскольку цена акции меняется со временем, то и стоимость выписанного опциона, обеспечивающего безрисковую сделку, также должна соответствующим образом изменяться. Из этих предположений можно получить оценку (вероятностную) стоимости опциона.
Работы Блэка и Шоулса, а также тесно связанные с ними работы Р. Мертона сразу же получили широкое признание. Более того, схемы расчетов, приведенные в этих работах, были очень быстро использованы на практике. Следует заметить, что 70-е гг. XX века — это годы чрезвычайно быстрого, «взрывного» роста рынка опционов. Так, за три года после открытия в 1973 г.
Чикагской опционной биржи число ежедневно заключаемых на ней контрактов возросло более чем в 100 раз.
Модель Блэка — Шоулса до сих пор остается одной из наиболее часто используемых, хотя со временем появились более сложные модели, как опционов, так и других производных ценных бумаг. Не смотря на то, что первые работы Блэка — Шоулса и Мертона были посвящены оценке стоимости опционов, они оказали чрезвычайно большое влияние и на другие разделы финансовой математики.
В целом, 70-е гг. прошлого столетия, характеризуются стремительным расширением и углублением математических средств финансового анализа. Но пик математизации финансового анализа был достигнут в 80-90-х гг., когда в исследованиях стали применять весьма тонкие и сложные средства современной теории случайных процессов и оптимального управления. Дальнейшее развитие инвестиционной теории шло по пути совершенствования разработанных классических моделей оптимального портфеля.
История развития инвестиционной теории по понятным причинам касается лишь работ, сделанных на Западе, прежде всего в США. Однако интерес к современной теории инвестиций и теории финансов постоянно растет и в нашей стране. Появляются работы как общего характера, посвященные рынку ценных бумаг, описанию различных финансовых и инвестиционных сделок, так и специального характера, например, по фьючерсам и опционам. Появились и работы по применению математических методов в финансовом деле.
Все результаты, полученные в инвестиционной теории, основаны на подходе, сформулированном в работах Марковица, сущность этого подхода заключается в том, что портфель ценных бумаг формируется на основе соотношения риск — доходность или тех или иных комбинаций риска и доходности. Примером этого может служить работа И. Волошина «Var -подход к поиску оптимального портфеля активов», где изложен подход к формированию портфеля ценных бумаг, исключающий необходимость построения множества эффективных портфелей и кривых безразличия. В качестве критерия оптимизация портфеля он использует линейную свертку ожидаемой доходности и риска, измеряемого средним квадратическим отклонением доходности ценной бумаги.
Достаточно подробно вопросы адаптации результатов классических теорий портфельного инвестирования к российскому фондовому рынку изложены в работе профессора Б. Рязанова «Теории портфельного инвестирования и их применение в условиях российского рынка».
Процесс создания современной теории инвестиций еще далеко не закончен, продолжаются активное обсуждение и споры по поводу ее основных принципов и результатов. Очевидно одно, модель Марковича обладает огромным потенциалом по формированию инвестиционных стратегий с различной целевой установкой. Можно получить стратегии, удовлетворяющие острожных инвесторов, а можно получить стратегии для дерзких инвесторов. Модель может использоваться и для формирования самофинансируемой стратегии, используемой при оценке стоимости опциона. Новаторские идеи, заложенные Марковицем, продолжают способствовать развитию современной финансовой теории.
Глава 1.2. «Математические модели портфельных решений»
Для формального изложения теории портфельного инвестирования вводятся следующие обозначения: А = {А1,А2, …, А n} — есть множество активов (акций, облигаций, валютных единиц, всевозможных комбинаций активов), обращающихся на финансовом рынке; рыночную стоимость актива Аi в момент времени t будет обозначать Sit; а величину денежного потока (дивиденды, купонные выплаты и т.п.), связанного с активом Аi— в тот же самый момент времени — Dit.
Доходность представляет собой ту характеристику, которая больше всего интересует инвесторов на финансовом рынке. Она является случайной величиной. Поэтому для строгого математического описания ее поведения вводится вероятностное пространство (Ω,F,Р), где Ω, — множество элементарных исходов на финансовом рынке, F — множество событий, Р — вероятности на множестве событий. На формальном уровне все активы Ai финансового рынка в каждый момент времени описываются случайной величиной rit как функцией от ω ∈ Ω, т.е. rit = ri(ω).
В качестве данных для решения оптимизационной задачи нельзя использовать случайные величины. Поэтому обычно переходят к усредненным величинам: математическому ожиданию, дисперсии, ковариации.
Любой портфель из достижимого множества характеризуется в соответствии с подходом Марковица двумя показателями — математическим ожиданием и дисперсией.
Инвесторы стремятся сформировать портфели, обеспечивающие им высокую доходность с достаточно низким уровнем риска. Одновременно получить портфель, который обеспечивал бы достижение максимальной доходности и минимального риска невозможно. Поэтому задачи формирования портфеля, как правило, предусматривают оптимизацию одного из показателей при фиксированном уровне второго. Либо строится целевая функция, реализующая свертку этих критериев и тем самым сводящая многокритериальную (в данном случае двухкритериальную) задачу к однокритериальной.
Глава 2.1. Модели прогнозирования финансовых временных рядов в условиях гипотезы эффективного рынка.
Вопрос прогнозирования финансового рынка в условиях, когда выполняются предпосылки гипотезы эффективного рынка, и прост, и одновременно сложен. Если все предположения гипотезы выполняются, то это значит, что текущая цена установилась на таком уровне, в котором учтена вся доступная к этому моменту информация и изменение возможно только в случае появления новой информации.
Описание этой ситуации на формальном уровне выглядит следующим образом. Биржевые торги рассматривают как случайный эксперимент с элементарными исходами ωi в виде последовательности ω = (ω1, …,ωT). Это позволяет рассматривать в качестве математической модели торгов, растянутых до момента Т, вероятностное пространство (Ω, FT, Р), где Ω, — множество элементарных событий, FT — информационный поток, который историей рынка фиксируется в виде последовательности элементарных событий, Р —вероятностная мера. Если F0 ⊆ F1 ⊆ … ⊆ Ft поток доступной всем участникам финансового рынка информации, то цена финансового актива удовлетворяет следующему мартингальному соотношению
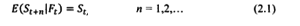
Это соотношение следует понимать как ситуацию, которая создается информационными возможностями на момент проведения прогнозных расчетов. Лучшим прогнозом цены на «завтра» является цена текущего момента. Пока нет информации о будущем, нет представления и о цене, которая будет иметь место в этом будущем. Причем даже полное представление о будущем не позволяет определить цену, которая будет иметь место в этом будущем. Необходимо, чтобы это будущее наступило и рыночные механизмы, ассимилировав информацию, изменили цены предыдущего момента времени. Другими словами, нужно знать не только информацию об ожидаемом будущем,
но и механизм, с помощью которого эта информация трансформируется в реальные цены.
Кроме того, если сегодняшняя информация о будущем становится достоянием всех участников рынка, то в соответствии с предположениями гипотезы эффективного рынка в ценах произойдут изменения не завтра, а сегодня.
В силу отмеченных обстоятельств мартингал оказался удобным инструментом для определения прогнозных значений. Его специфические свойства полностью находятся в соответствии с предположениями гипотезы эффективного рынка. В то же время эти специфические свойства являются тем фундаментом, на основе которого выстраивались предположения эффективного рынка, так как сама гипотеза формировалась одновременно с развитием аппарата моделирования финансовых рынков.
Мартингалы оказались удобным инструментом теоретических исследований. Они используются при выводе формулы Блэка — Шоулса и в модели биномиального рынка Кокса — Росса — Рубинштейна (CRR-модели). Но задача реального прогнозирования с помощью мартингалов не решается. В связи с этим возникает вопрос соответствия гипотезы реальностям рынка. Справедливость предположений гипотезы эффективного рынка проверяется путем тестирования. Традиционно подобная проверка сводится к тестированию того, следуют ли цены финансовых активов случайному блужданию. Для этого используются линейные модели временных рядов, рассмотрение которых будет осуществлено ниже. В последнее время для этих целей стал широко использоваться R/S -анализ. Как правило, выводы, получаемые с помощью этих двух подходов, получаются согласованными, и поэтому я буду использовать первый из них. Если гипотеза не подтверждается, то исследуются причины, лежащие в основе невыполнения предположений гипотезы.
Чаще всего такой причиной является наличие значимой автокорреляции в динамических рядах цен на активы. Это является признаком наличия ситуации, когда цены на финансовые активы частично прогнозируемы. Как
правило, в краткосрочном периоде, наблюдаемая автокорреляция положительная, а в долгосрочном — отрицательная. Предсказуемость цен на финансовом рынке противоречит гипотезе эффективного рынка, но позволяет с надеждой браться за решение задачи по формированию портфеля с условно ожидаемой доходностью.
Эмпирические исследования динамики финансовых рынков показывают, что автокорреляция может иметь место в рядах, характеризующих цены финансовых активов, и отсутствует в рядах, характеризующих доходности этих же активов. Таблица 2.1. наглядно демонстрирует ситуацию, в соответствии с которой в динамических рядах цен наблюдается высокая автокорреляция, а в динамических рядах доходностей автокорреляция отсутствует.
Таблица 2.1 Автокорреляции цен и доходностей акций
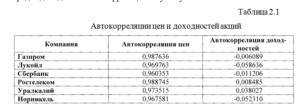
При построении портфелей ценных бумаг используются доходности и, естественно, реализация разрабатываемого подхода, ориентируемого на использование прогнозных оценок, требует, чтобы по всем акциям, включаемым в портфель, имелись упреждающие оценки доходности. К сожалению, как показали результаты эмпирических исследований, ряды из доходностей акций представляют собой результат случайных блужданий и, следовательно, не пригодны для построения прогнозных моделей. В то же время, динамические ряды из цен вполне прогнозируемы и может сложиться точка зрения, в соответствии с которой прогнозную доходность следует получать из соответствующих прогнозных оценок цены. В принципе такой вариант прогнозных расчетов доходности вполне реализуем. Однако точность оконча-
тельного результата оказывается заниженной как минимум в два раза по сравнению с точностью, используемой для этих целей модели. Поэтому практическая ценность данного варианта близка к нулю.
Для построения портфеля ценных бумаг, структура которого ориентирована на ожидаемую доходность в упреждающем инвестиционном периоде, информация по ежедневным доходностям не требуется. В модели формирования оптимального портфеля используются числовые характеристики случайных величин, а не сами случайные величины. Поэтому имеет смысл прогнозировать средние характеристики того периода, в котором инвестор надеется получить доход от средств, вложенных в портфель, используя для этого данные исторического периода.
Вопрос предварительного преобразования данных и переход к временным рядам, уровни которых являются усредненными характеристиками исходных временных рядов, решен однозначно в пользу усреднения. Но его решение ставит еще ряд вопросов, на которые нет однозначных ответов. Смысл первого вопроса в том, чтобы выяснить, какое количество наблюдений рационально использовать для получения каждого усредненного значения. Теоретически обоснованных рекомендаций по этому поводу нет. Скорее всего, в каждом конкретном случае должны проводиться специальные эмпирические исследования. Понятно, что рост числа слагаемых приводит к увеличению автокорреляции, но есть и предел значимого увеличения.
Второй вопрос касается способа усреднения. Например, процедуру усреднения можно построить следующим образом: первое усредненное значение получить как среднее первых десяти наблюдений, второе — вторых десяти наблюдений и т.д.
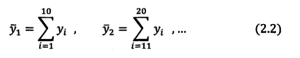
Другой способ усреднения основан на использовании принципа скользящего усреднения, предусматривающего выбывание из множества усред-няемых величин самого раннего наблюдения и включение наблюдения следующего за последним элементом этого множества, т.е.
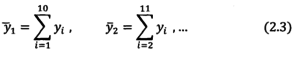
Второй подход предпочтительней первого, так как целенаправленно формирует временной ряд, обладающий памятью и, следовательно, заведомо прогнозируемый. Результаты эмпирических исследований, приведенные в таблице 2.2., подтверждают эту точку зрения.няемых величин самого раннего наблюдения и включение наблюдения следующего за последним элементом этого множества, т.е.
Таблица 2.2
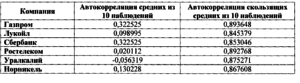
Сравнение коэффициентов автокорреляции средних и скользящих средних
В отличие от временных рядов из средних значений, имеющих низкую автокорреляцию, по всем временным рядам из скользящих средних наблюдается высокий уровень автокорреляции. Природа этой автокорреляции понятна. Временной ряд из скользящих средних значений сформирован таким образом, и это отмечалось выше, что в нем индуцируется память. Причем глубина памяти и уровень автокоррелированности явно взаимосвязанные характеристики. Это хорошо иллюстрируется расчетами, результаты которых приведены в таблице 2.3.
Если за глубину памяти принять размер окна скольжения без единицы (первая строка), то значения каждой строки данной таблицы можно интерпретировать как автокорреляционные коэффициенты, которые наблюдаются во временных рядах, обладающих соответствующей глубиной памяти. Интересно отметить, что коэффициенты автокорреляции всех ценных бумаг соответствующие одной и той же глубине памяти мало отличаются друг от друга. Это свойство играет важную роль в реализации идеи построения портфелей на основе прогнозных оценок, так как, по сути, обеспечивает возможность получения прогнозных оценок одинаковой надежности.
Таблица 2.3 Зависимость уровня автокоррелированности от глубины памяти
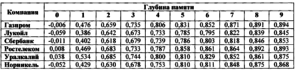
Проблема равной надежности данных по всем котировкам акций, включаемых в портфель, обычно не рассматривается, так как все средние, на основе которых строится портфель, обладают одним и тем же уровнем надежности. В рассматриваемом подходе портфель строится с использованием условно средних величин, надежность которых находится в прямой зависимости от адекватности эконометрической модели. Поэтому желательно, чтобы прогнозные оценки по всем акциям были равнонадежными. Использование временных рядов из скользящих средних обеспечивает получение равно-надежных прогнозных оценок. Этот факт подтверждается результатами эмпирических исследований.Второй вопрос, который хотелось бы рассмотреть подробнее, связан с существованием взаимосвязи между уровнем автокорреляции и глубиной памяти. Из данных, приведенных в таблице 2.З., без сомнения следует, что увеличение глубины памяти вызывает в среднем рост коэффициентов авторегрессии. Закономерность данного роста имеет ярко выраженную тенденцию затухания. Это хорошо видно на рисунке 2.1. Анализ этого графика позволяет сделать вывод, что бесконечное наращивание памяти нецелесообразно, поскольку то увеличение коэффициента автокорреляции, которое получается в результате очередного наращения памяти, становится статически незначимым.
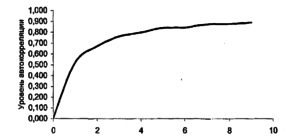
Рисунок 2.1. Зависимость уровня автокорреляции от глубины памяти
По данным таблицы 2.3. с помощью метода наименьших квадратов можно идентифицировать закономерность между значениями коэффициентов автокорреляции и глубиной памяти в виде степенной зависимости.
р=0,5242т0,2619
Где р — значение коэффициента автокорреляции; т — глубина памяти.
Построенная на основе эмпирических данных зависимость показывает, что прирост памяти на 1% увеличивает в среднем прирост значения коэффициента автокорреляции на 0,26%. Из этого можно сделать вывод, что рост коэффициента автокорреляции происходит гораздо медленнее, чем увеличивается память. Следовательно, высокий уровень автокорреляции можно обеспечить достаточно большой глубиной памяти. Вопрос о пределах этой глубины решается, как правило, по результатам эмпирических исследований. Строгих рекомендаций по поводу выбора размеров «окна» скользящего усреднения нет. Если эти размеры неограниченно увеличивать, то значение скользящего среднего будет приближаться к значению текущего среднего. В принципе прогноз текущего среднего тоже может использоваться при реализации рассматриваемого подхода, но его динамика более консервативна, чем динамика скользящего среднего. Поэтому вопрос определения размера «окна» скользящего усреднения имеет смысл связывать с инвестиционным горизонтом формируемого портфеля.
Далее рассмотрены модели, которые целесообразно применять для формирования портфеля с условно ожидаемой доходностью. Чаще всего для прогнозирования динамики эффективного рынка используются авторегрессионные модели
где уt — значение скользящего среднего в момент времени t;
а0, аi — оцениваемые коэффициенты авторегрессионной модели;
р — порядок авторегрессионной модели;
εt — ненаблюдаемая случайная величина в момент времени t.
Одна из проблем, которую приходится решать при построении авторегрессионной модели, связана с определением ее порядка. Решается эта проблема стандартным образом по значению частной автокорреляционной функции. В практических расчетах для этих целей используют последний авторегрессионный коэффициент модели. Если в модели (р +1) — го порядка последний коэффициент незначим, то модель имеет порядок р.
Вопрос о порядке авторегрессионной модели, построение которой осуществляется на основе данных, представляющих собой временные ряды скользящих средних, не актуален. Структура памяти этих временных рядов такова, что при построении моделей выше первого порядка проявляется эффект мультиколлинеарности. Все это не трудно проиллюстрировать на примере любой из ценных бумаг (таблица 2.4)
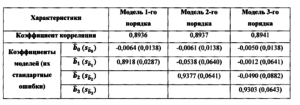
Таблица 2.4 Характеристика авторегрессионных моделей для акций Газпрома
Приведенные в таблице 2.4. результаты вычислительного эксперимента подтверждают точку зрения о том, что построению «хороших» моделей, порядок которых выше 1-го, мешает эффект мультиколлинеарности. Применение специальных процедур для устранения этого эффекта следует признать в данной ситуации нецелесообразным. Например, ридж-оценивание позволит убрать искажения, явно присутствующие в стандартных ошибках авторегрессионных коэффициентов, но одновременно внесет искажения в оценки самих коэффициентов.
Таким образом, в ситуациях, когда есть основание считать гипотезу эффективного рынка справедливой, для прогнозирования усредненных характеристик, используемых при построении портфеля ценных бумаг, целесообразно использовать авторегрессионные модели 1-го порядка.
Страница: 1 2
