Содержание
Введение
§1. Основные характеристики поверхности вращения.
§2. Омбилические точки поверхности вращения.
§3. Замечательные линии поверхности вращения.
§4. Поведение геодезических на некоторых поверхностях вращения.
§5. Обобщения поверхности вращения.
Заключение
Список используемых источников
Введение
Поверхности вращения представляют важную группу поверхностей, которые широко применяются в практике, что объясняется распространенностью вращательного движения, простотой обработки поверхностей вращения на станках.
Поверхности вращения образуются вращением линии (образующей) вокруг неподвижной оси. Образующей может быть как кривая линия, так и прямая линия. Это означает, что поверхности вращения могут быть как линейчатыми, так и нелинейчатыми.
Общий вид поверхности вращения представлен на рис. 1.
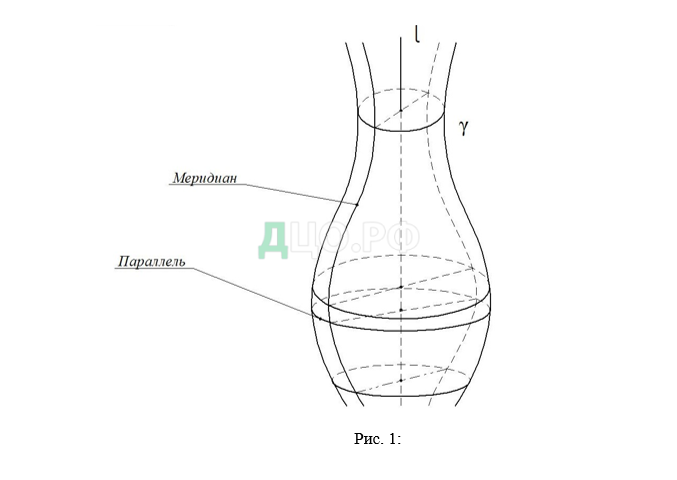
Эта поверхность имеет криволинейную образующую которая вращается вокруг вертикальной оси Каждая точка образующей линии при вращении
вокруг оси описывает окружность. Плоскости, перпендикулярные к оси пересекают поверхность вращения по окружностям, которые называются параллелями.
Любая плоскость, содержащая ось вращения пересекает поверхность вращения по линиям, которые называются меридианами.
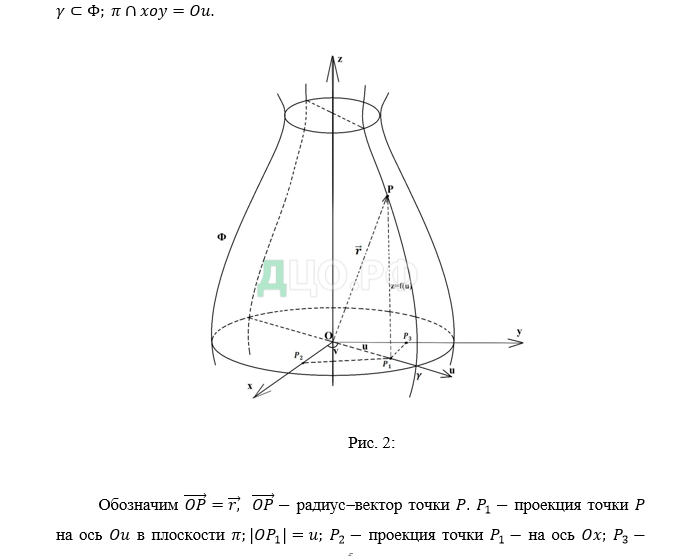
Введём уравнение поверхности вращения Выберем в пространстве прямоугольную декартову систему координат так, что ось совпадает с осью вращения поверхности Проведём через плоскость где меридиан поверхности В плоскости введём прямоугольную декартову систему координат (см. рис. 2) Допустим, что регулярная кривая, задаваемая уравнением Возьмем на линии произвольную точку









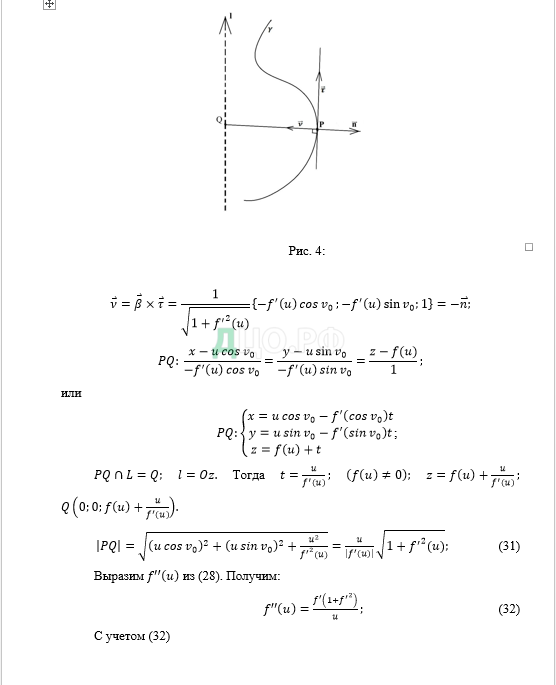















Заключение
Поверхности вращения широко используются в технике, машиностроении, быту, строительстве, архитектуре, прикладном искусстве, а также в преподавании геометрии в школе и в вузе. Такое широкое применение поверхностей вращения объясняется простотой их формообразования: многие из них обрабатываются на станках при относительном вращательном движении режущего или формирующего инструмента и изделия.
Многие изделия представляют собой тела вращения: шарики в шарикоподшипниках, оси, валы резьбовые детали, шайбы, штифты, пробки, фрезы-шарошки, круглые фасонные напильники, абразивные фасонные головки. Многие конструктивные элементы технических деталей ограничены поверхностями вращения: буртики, гнезда, отверстия, проточки, фаски.
В технике широко применяются линейчатые поверхности вращения. Например, в строительной технике часто используют однополостный гиперболоид вращения, имеющий два семейства прямолинейных образующих. Корпуса многих космических кораблей имеют форму поверхностей вращения. Звукоулавливатели, радиотелескопы, прожектора и фары автомобилей имеют форму параболоидов вращения.
В настоящее время поверхность вращения, изучается и применяется инженерами-конструкторами, художниками-прикладниками, архитекторами, строителями, физиками, астрономами и многими другими специалистами.
В дипломной работе представлены основные факты и доказаны теоремы, описывающие свойства поверхностей вращения. А именно: в первом параграфе описаны их основные характеристики; параграф два посвящен изучению омбилических точек поверхности вращения с использованием индикатрисы Дюпена; в третьем и четвертом параграфах изучены все замечательные линии поверхности (асимптотические линии, линии кривизны и геодезические линии); пятый параграф содержит информацию о существующих обобщениях поверхностей вращения.
Список используемых источников
- Выгодский М.Я. Справочник по высшей математике. — М.: АСТ: Астрель, 2021. 703с.
- Дарбу Ж.Г. Лекции по общей теории поверхностей и геометрические приложения анализа бесконечно малых. Т. I. Общие понятия. Криволинейные координаты. Минимальные поверхности. -М. — Ижевск: Институт компьютерных исследований, 2013. 620с.
- Дарбу Ж.Г. Лекции по общей теории поверхностей и геометрические приложения анализа бесконечно малых: в 4-х томах. ТОМ 3: Геодезические линии и геодезическая кривизна. Дифференциальные параметры. Изгибание поверхности. Т.3. — М. — Ижевск: Институт компьютерных исследований, 2013. 516с.
- Джусти Э. Минимальные поверхности и функции ограниченной вариации. М.: Изд-во «Мир» 1989. 240 с.
- Егоров Д.Ф. Дифференциальная геометрия. Изд. 2-е. М.: Изд-во URSS. 2022. 304с.
- Жукова Н.И., Багаев А.В. Геодезические линии на поверхностях: Учеб. пособие. Новгород: Изд-во Нижегородского университета, 2008. 54с.
- Игнатьев Ю.Г. Дифференциальная геометрия кривых в евклидовом пространстве: Учеб. Пособие — Казань: Изд-во Казанский университет, 2013. 204с.
- Каган В.Ф. Основы теории поверхностей в тензорном изложении. Ч.2: Поверхности в пространстве. Отображения и изгибания поверхностей. Специальные вопросы. Изд. 2-е. — М.:ЛЕНАНД, 2021. 408с.
- Норден А.П. Краткий курс дифференциальной геометрии. Изд. 3-е. М.: Изд-во ФИЗМАТГИЗ, 2019. 248с.
- Норден А.П. Теория поверхностей. Изд. 2-е. М.: Изд-во Гостехиздат., 2019. 264с.
- Оссерман Р. Минимальные поверхности. М.: Изд-во Физматлит, 2020. 352с.
- Погорелов А.В. Внешняя геометрия выпуклых поверхностей. М.: Наука, 1969. 760с.
- Погорелов, А. В.Дифференциальная геометрия. Изд. 7-е. М.: Изд-во URSS, 2022. 184с.
- Поздняк Э.Г. Шикин Е.В. Дифференциальная геометрия первое знакомство. М.: Изд-во МГУ, 2003. 408с.
- Розендорн Э.Р. Теория поверхностей. Изд. 2-е, перераб. и доп. М.: Изд-во Физматлит, 2006. 304с.
- Топоногов В.А. Дифференциальная геометрия кривых и поверхностей. М.: Изд-во: Физматкнига, 2012. 224с.
- Фиников С.П. Курс дифференциальной геометрии. Изд. 4-е. М.: КомКнига, 2013. 344с.
- Фиников С.П. Теория поверхностей. Изд. 4-е, перераб., испр. М.: Либроком, 2018. 304с.
- Шарипов Р.А. Курс дифференциальной геометрии: учебное пособие для вузов: Издание Башкирского университета. — Уфа, 1996. 211с.
- Thomas F. Banchoff, Stephen T.Lovett Differential Geometry of Curves and Surfaces: Publisher CRC Press, 2016 yr. 430p.
