1.4.2.2 Криптосистема Эль-Гамаля
Данная система является альтернативой RSA и при равном значении ключа обеспечивает ту же криптостойкость [7. С. 56].
В отличие от RSA метод Эль-Гамаля основан на проблеме дискретного логарифма. Этим он похож на алгоритм Диффи-Хелмана. Если возводить число в степень в конечном поле достаточно легко, то восстановить аргумент по значению (то есть найти логарифм) довольно трудно.
Основу системы составляют параметры p и g – числа, первое из которых – простое, а второе – целое.
Участник А генерирует секретный ключ а и вычисляет открытый ключ y = gа mod p. Если участник В хочет послать участнику А сообщение m, то он выбирает случайное число k, меньшее p и вычисляет
y1 = gk mod p и
y2 = m Å yk,
где Å означает побитовое сложение по модулю 2. Затем участник В посылает (y1, y2) участнику А.
Участник А, получив зашифрованное сообщение, восстанавливает его:
m = (y1a mod p) Å y2.
Алгоритм цифровой подписи DSA, разработанный NIST (National Institute of Standard and Technology) и являющийся частью стандарта DSS частично опирается на рассмотренный метод.
1.4.2.3 Криптосистемы на основе эллиптических уравнений
Эллиптические кривые – математический объект, который может определен над любым полем (конечным, действительным, рациональным или комплексным). В криптографии обычно используются конечные поля. Эллиптическая кривая есть множество точек (x, y), удовлетворяющее следующему уравнению [7. С. 69]:
y2 = x3 + ax + b,
а также бесконечно удаленная точка. Для точек на кривой довольно легко вводится операция сложения, которая играет ту же роль, что и операция умножения в криптосистемах RSA и Эль-Гамаля.
В реальных криптосистемах на базе эллиптических уравнений используется уравнение
y2 = x3 + ax + b mod p, где р – простое.
Проблема дискретного логарифма на эллиптической кривой состоит в следующем: дана точка G на эллиптической кривой порядка r (количество точек на кривой) и другая точка Y на этой же кривой. Нужно найти единственную точку x такую, что Y = xG, то есть Y есть х-я степень G.
1.5 Сравнительные характеристики алгоритмов шифрования
Программная реализация криптоалгоритмов типа RSA значительно сложнее и менее производительна, чем реализация классических криптоалгоритмов типа DES. Вследствие сложности реализации операций модульной арифметики криптоалгоритм RSA часто используют только для шифрования небольших объемов информации, например для рассылки классических секретных ключей или в алгоритмах цифровой подписи, а основную часть пересылаемой информации шифруют с помощью симметричных алгоритмов [5. С. 105].
В табл. 5 приведены некоторые сравнительные характеристики классического криптоалгоритма DES и криптоалгоритма RSA.
Табл. 5. Сравнительные характеристики DES и RSA
| Характеристика | DES | RSA |
| Скорость шифрования | Высокая | Низкая |
| Используемая функция шифрования | Перестановка и подстановка | Возведение в степень |
| Длина ключа | 56 бит | Более 500 бит |
| Наименее затратный криптоанализ (его сложность определяет стойкость алгоритма) | Перебор по всему ключевому пространству | Разложение числа на простые множители |
| Время генерации ключа | Миллисекунды | Минуты |
| Тип ключа | Симметричный | Асимметричный |
1.6 Наиболее устойчивые к взлому алгоритмы шифрования
Следующие разработки всемирно признаны стойкими алгоритмами и публикаций о универсальных методах их взлома в средствах массовой информации не встречалось (Табл. 6) [19. С. 33].
Табл. 6. Устойчивые к взлому алгоритмы шифрования
| Название алгоритма | Автор | Размер блока | Длина ключа |
| IDEA | Xuejia Lia and James Massey | 64 бита | 128 бит |
| CAST128 | 64 бита | 128 бит | |
| BlowFish | Bruce Schneier | 64 бита | 128 – 448 бит |
| ГОСТ | НИИ *** | 64 бита | 256 бит |
| TwoFish | Bruce Schneier | 128 бит | 128 – 256 бит |
| MARS | Корпорация IBM | 128 бит | 128 – 1048 бит |
Криптоалгоритм именуется идеально стойким, если прочесть зашифрованный блок данных можно только перебрав все возможные ключи, до тех пор, пока сообщение не окажется осмысленным. Так как по теории вероятности искомый ключ будет найден с вероятностью 1/2 после перебора половины всех ключей, то на взлом идеально стойкого криптоалгоритма с ключом длины N потребуется в среднем 2N-1 проверок. Таким образом, в общем случае стойкость блочного шифра зависит только от длины ключа и возрастает экспоненциально с ее ростом. Даже предположив, что перебор ключей производится на специально созданной многопроцессорной системе, в которой благодаря диагональному параллелизму на проверку 1 ключа уходит только 1 такт, то на взлом 128 битного ключа современной технике потребуется не менее 1021 лет. Естественно, все сказанное относится только к идеально стойким шифрам, которыми, например, с большой долей уверенности являются приведенные в таблице выше алгоритмы.
Кроме этого условия к идеально стойким криптоалгоритмам применяется еще одно очень важное требование, которому они должны обязательно соответствовать. При известных исходном и зашифрованном значениях блока ключ, которым произведено это преобразование, можно узнать также только полным перебором. Ситуации, в которых постороннему наблюдателю известна часть исходного текста встречаются повсеместно. Это могут быть стандартные надписи в электронных бланках, фиксированные заголовки форматов файлов, довольно часто встречающиеся в тексте длинные слова или последовательности байт.
1.7 Идентификация и аутентификация пользователей
Расширение круга пользователей распределенных систем и усложнение задач, решаемых с помощью подобных сетей, привели к осознанию первостепенной важности проблем, связанных с обеспечением информационной безопасности при межсетевом взаимодействии, прежде всего с использованием открытых каналов передачи данных, создающих потенциальную возможность для действий как пассивного нарушителя, имеющего возможность только просматривать доступные ему сообщения, так и активного нарушителя, который наряду с прослушиванием может модифицировать доступные ему сообщения [6. С. 120-135].
Вот почему одной из важнейших задач обеспечения безопасности является разработка методов и средств, позволяющих одной стороне (проверяющему) убедиться в идентичности другой стороны (доказывающего).
Прежде чем получить доступ к ресурсам компьютерной системы, пользователь должен пройти процесс представления компьютерной системе, который включает две стадии:
- идентификацию – пользователь сообщает системе по ее запросу свое имя (идентификатор);
- аутентификацию – пользователь подтверждает идентификацию, вводя в систему уникальную, не известную другим пользователям информацию о себе (например, пароль).
С точки зрения проверяющего к аутентификации предъявляются следующие критичные требования:
- при взаимном доверии сторон А и В стороне А необходимо убедиться в идентичности стороны В;
- сторона В не должна иметь возможность повторного обмена информацией, переданной ранее в ходе взаимодействия со стороной А, с целью выдать себя за сторону А при аутентификации со стороны С;
- различия в аутентификационном обмене между сторонами должны быть настолько существенными, чтобы ни одна из сторон не смогла реализовать обмен данными от имени другой стороны;
- информация пересылаемая в рамках аутентификационного обмена, должна препятствовать получению статистических сведений, на основе которых пассивный нарушитель смог бы имитировать обмен от имени какой-либо стороны, т.е. в результате информационного обмена знания участников друг о друге не должны увеличиваться.
Все аутентификации могут быть разделены на следующие категории [3. С. 91-98]:
- на основе знания чего-либо. Примером могут служить стандартные пароли, персональные идентификационные номера (PIN), а также секретные и открытые ключи;
- на основе обладания чем-либо. Обычно это магнитные карты, смарт-карты, touch memory и персональные генераторы, которые используются для создания одноразовых паролей.
- на основе каких-либо неотъемлемых характеристик. Эта категория включает методы, базирующиеся на проверке пользовательских биометрических характеристик (голос, сетчатка глаза, отпечатки пальцев). В данной категории не используются криптографические методы и средства. Аутентификация на основе биометрических характеристик применяется для контроля доступа в помещения либо к какой-либо технике.
В табл. 7 приведены основные типы аутентификации пользователей
Табл. 7. Основные типы аутентификации пользователей
| Тип | Описание |
| Пароли или PIN-коды (персональные идентификационные номера) |
Что-то, что знает пользователь и что также знает другой участник взаимодействия.
Обычно аутентификация производится в 2 этапа. Может организовываться обмен паролями для взаимной аутентификации. |
| Одноразовый пароль | Пароль, который никогда больше не используется.
Часто используется постоянно меняющееся значение, которое базируется на постоянном пароле. |
| CHAP (протокол аутентификации запрос-ответ) |
Одна из сторон инициирует аутентификацию с помощью посылки уникального и непредсказуемого значения «запрос» другой стороне, а другая сторона посылает вычисленный с помощью «запроса» и секрета ответ. Так как обе стороны владеют секретом, то первая сторона может проверить правильность ответа второй стороны. |
| Встречная проверка (Callback) |
Телефонный звонок серверу и указание имени пользователя приводит к тому, что сервер затем сам звонит по номеру, который указан для этого имени пользователя в его конфигурационных данных. |
Говоря о классификации по уровню обеспечиваемой безопасности, необходимо упомянуть о типовых атаках на аутентификацию и общих методах, помогающих их избежать (табл. 8) [19. С. 152-159]
Табл. 8. Типовые атаки на аутентификацию и их пути обхождения
| Тип атаки | Пути обхождения |
| 1. Повторная передача. Заключается в повторной передаче аутентификационных данных каким-либо пользователем | Использование протоколов типа «запро-ответ»; использование меток времени или случайных чисел; вставка идентифицирующей информации в ответы |
| 2. Подмена стороны аутентификационного обмена. Злоумышленник в ходе данной атаки участвует в процессе аутентификационного обмена между двумя сторонами и имеет возможность модификации проходящего через него трафик | Связывание всех сообщений в рамках данной сессии (например, используя одноразовый и уникальный идентификатор во всех сообщениях) |
| 3. Отражение передачи. Один из вариантов предыдущей атаки, в ходе которой злоумышленник в рамках данной сессии пересылает обратно перехваченную информацию | Использование идентификаторов сторон в передаваемых сообщения; построение формы таки образом, чтобы каждое сообщение имело отличную от других форму |
| 4. Выборка текста. Злоумышленник перехватывает аутентификационный трафик и пытается получить информацию о долговременных ключах | Использование протоколов, обладающих свойством доказательства нулевым знанием; включение в сообщение случайных чисел |
| 5. Задержка передачи. Злоумышленник перехватывает некоторую информацию и передает ее спустя некоторое время | Комбинирование использования меток времени вместе со случайными числами |
Самая опасная угроза аутентификации возникает в том случае, когда нарушитель выдает себя за какую-либо другую сторону, обычно обладающими существенными привилегиями в системе. Именно получение привилегий и возможность работы от лица другого пользователя (в случае, если в системе используется система аудита) являются основными целями злоумышленника.
Учитывая описанные выше атаки, а также вопросы практического применения, можно выделить следующие свойства аутентификации [4. С. 134-137]:
- взаимная аутентификация. Свойство, отражающее необходимость обоюдной аутентификации между сторонами аутентификационного обмена;
- вычислительная эффективность. Количество операций, необходимых для выполнения аутентификации;
- коммуникационная эффективность. Данное свойство отражает количество сообщений и их длину, необходимую для осуществления аутентификации;
- наличие третьей стороны. Примеров третьей стороны может служить доверенный сервер распределения симметричных ключей или сервер, реализующий дерево сертификатов для распределения открытых ключей;
- основа гарантий безопасности. Примером могут служить протоколы, обладающие свойством доказательства с нулевым знанием;
- хранение секрета. Здесь имеется в виду, каким способом реализовано хранение критичной ключевой информации.
Одной из основных задач, решаемых во время работы подобных протоколов, является разграничение доступа к ресурсам, когда при привилегированном доступе необходимо убедиться в идентичности пользователей (например, локальный или удаленный доступ к ресурсам компьютера или доступ к приложениям со стороны пользователей).
1.8 Электронно-цифровая подпись
Последние несколько лет ознаменовались постепенной заменой бумажной технологии обработки информации ее электронным аналогом. Со временем можно ожидать полного вытеснения бумажного документооборота электронным [26. С. 156-160]. Однако представление традиционных бумажных документов в виде электронных последовательностей, состоящих из нулей и единиц, обезличивает последние. Защитных атрибутов бумажных документов: подписей, печатей и штампов, водяных знаков, специальной фактуры бумажной поверхности, — у электронного представления документов нет. Но электронные документы нужно защищать не менее тщательно, чем бумажные. Поэтому возникает задача разработки такого механизма электронной защиты, который бы смог заменить подпись и печать на бумажных документах. То есть необходимо разработать механизм электронно-цифровой подписи, которая представляет собой дополнительную информацию, приписываемую к защищаемым данным. Цифровая подпись зависит от содержания подписываемого документа и некоего секретного элемента (ключа), которым обладает только лицо, участвующее в защищенном обмене.
Такой механизм обеспечивает:
- Во-первых, цифровая подпись должна подтверждать, что подписывающее лицо не случайно подписало электронный документ.
- Во-вторых, цифровая подпись должна подтверждать, что только подписывающее лицо, и только оно, подписало электронный документ.
- В-третьих, цифровая подпись должна зависеть от содержания подписываемого документа и времени его подписания.
- В-четвертых, подписывающее лицо не должно иметь возможности в последствии отказаться от факта подписи документа.
1.8.1 Электронно-цифровая подпись при помощи симметричных криптосистем
Первые варианты цифровой подписи были реализованы при помощи симметричных криптосистем, в которой абоненты, участвующие в обмене сообщениями, используют один и тоже секретный ключ для простановки и проверки подписи под документом. В качестве алгоритма криптографического преобразования может использоваться любая из симметричных криптосистем, обладающая специальными режимами функционирования (например, DES, ГОСТ 28147-89 и т.п.) [3. С. 123-130].
Процедура подписи документов при помощи симметричной криптосистемы может выглядеть следующим образом:
- Отправитель А и получатель В обладают одинаковым секретным ключом K.
- Отправитель А зашифровывает цифровое сообщение, используя ключ K, и посылает зашифрованное сообщение получателю В. При этом, как уже отмечалось, используется криптосистема, обладающая специальными механизмами функционирования, например ГОСТ 28147-89 в режиме выработки имитовставки.
- Получатель В расшифровывает сообщение при помощи ключа K.
Так как только пользователи А и В обладают секретным ключом, то тем самым обеспечивается гарантия, что сообщение подписано именно пользователем А, а не злоумышленником C. Однако, данная схема применима только в тех сетях, в которых можно дать стопроцентную гарантирую надежности каждого из абонентов, т.к. в обратном случае существует потенциальная возможность мошенничества со стороны одного из абонентов, владеющих секретным ключом.
Для устранения указанного недостатка была предложена схема с доверенным арбитром. В данной схеме помимо пользователей А и В существует арбитр – X. X может обмениваться сообщениями и с отправителем А и с получателем В, и владеет секретными ключами обоих — KА и KB. Процедура подписания документов в данной схеме выглядит следующим образом:
- Отправитель А зашифровывает сообщение, используя ключ KА, и посылает его арбитру X.
- Арбитр X расшифровывает сообщение, также используя ключ KА.
- Расшифрованное сообщение арбитр X зашифровывает на ключе получателя В KВ.
- Данное сообщение арбитр X посылает получателю В.
- Получатель В расшифровывает сообщение, полученное от арбитра X, используя ключ KВ.
Насколько эффективна данная схема? Рассмотрим ее с учетом вышеуказанных требований, предъявляемых к цифровой подписи:
- Во-первых, арбитр X и получатель В знают, что сообщение пришло именно от отправителя А. Уверенность арбитра X основана на том, что секретный ключ KА имеют только отправитель А и арбитр X. Подтверждение арбитра X служит доказательством получателю В.
- Во-вторых, только отправитель А знает ключ KА (и арбитр X, как доверенный арбитр). Арбитр X может получить зашифрованное сообщение на ключе KА только от отправителя А. Если злоумышленник С пытается послать сообщение от имени отправитель А, то арбитр X сразу обнаружит это на 2-м шаге.
- В-третьих, если получатель В пытается использовать цифровую подпись, полученную от арбитра X, и присоединить ее к другому сообщению, выдавая его за сообщение от отправителя А, это выявляется. Арбитр X может потребовать от получателя В данное сообщение и затем сравнивает его с сообщением, зашифрованном на ключе KА. Сразу выявляется факт несоответствия между двумя сообщениями. Если бы получатель В попытался модифицировать присланное сообщение, то арбитра X аналогичным способом выявила бы подделку.
- В-четвертых, даже если отправитель А отрицает факт посылки подписанного сообщения, подтверждение от арбитра X говорит об обратном.
Можно заметить, что самым критичным звеном этой схемы является именно арбитр X. Во-первых, он должен быть действительно независимой ни от кого стороной. А во-вторых, арбитр X должен быть абсолютно безошибочным. Ошибка в рассмотрении даже одной из нескольких тысяч спорных ситуаций подорвет доверие не только к арбитру X, но и ко всем предыдущим подписанным документам, достоверность которых удостоверялась арбитром X.
Именно поэтому, несмотря на теоретическую возможность применения симметричных криптосистем, на практике для выработки подписи они не используются, поскольку требуют дорогостоящих и громоздких мероприятий по поддержанию достаточного уровня достоверности передаваемых данных.
1.8.2 Электронно-цифровая подпись при помощи асимметричных криптосистем
В таких криптосистемах нет необходимости и в арбитрах. Суть этого подхода заключается в том, что в обмене защищаемыми документами каждый абонент использует пару взаимосвязанных ключей – открытый и секретный. Отправитель подписываемого документа передает получателю открытый ключ. Он может это сделать любым несекретным способом или поместить ключ в общедоступный справочник. При помощи открытого ключа получатель проверяет подлинность получаемой информации. Секретный ключ, при помощи которого подписывалась информация, хранится в тайне от всех [5. С. 142-148].
Можно заметить, что в данной схеме абоненты используют различные ключи, что не позволяет мошенничать ни одной из сторон. Подробный анализ цифровой подписи на основе криптосистем с открытыми ключами показывает, что она полностью удовлетворяет требованиям, предъявляемым к ней. В настоящий момент широкого известны цифровые подписи, построенные по алгоритмам RSA, Эль-Гамаля, Шнорра, Рабина и математического аппарата эллиптических кривых.
В табл. 9 представлены основные типы электронно-цифровой подписи. Добавление временных меток позволяет обеспечить ограниченную форму контроля участников взаимодействия.
Табл. 9. Основные типы электронно-цифровой подписи
| Тип | Комментарии |
| DSA (Digital Signature Authorization) |
Алгоритм с использованием открытого ключа для создания электронной подписи, но не для шифрования.
Секретное создание хэш-значения и публичная проверка ее — только один человек может создать хэш-значение сообщения, но любой может проверить ее корректность. Основан на вычислительной сложности взятия логарифмов в конечных полях. |
| RSA | Запатентованная RSA электронная подпись, которая позволяет проверить целостность сообщения и личность лица, создавшего электронную подпись.
Отправитель создает хэш-функцию сообщения, а затем шифрует ее с использованием своего секретного ключа. Получатель использует открытый ключ отправителя для расшифровки хэша, сам рассчитывает хэш для сообщения, и сравнивает эти два хэша. |
| MAC (код аутентификации сообщения) |
Электронная подпись, использующая схемы хэширования, аналогичные MD или SHA, но хэш-значение вычисляется с использованием как данных сообщения, так и секретного ключа. |
| DTS (служба электронных временных меток) |
Выдает пользователям временные метки, связанные с данными документа, криптографически стойким образом. |
1.9 Хеширование паролей
Хеширования паролей – это метод, позволяющей пользователям запоминать не 128 байт, то есть 256 шестнадцатеричных цифр ключа, а некоторое осмысленное выражение, слово или последовательность символов, называющуюся паролем. Действительно, при разработке любого криптоалгоритма следует учитывать, что в половине случаев конечным пользователем системы является человек, а не автоматическая система. Это ставит вопрос о том, удобно, и вообще реально ли человеку запомнить 128-битный ключ (32 шестнадцатеричные цифры). На самом деле предел запоминаемости лежит на границе 8-12 подобных символов, а, следовательно, если мы будем заставлять пользователя оперировать именно ключом, тем самым мы практически вынудим его к записи ключа на каком-либо листке бумаги или электронном носителе, например, в текстовом файле. Это, естественно, резко снижает защищенность системы [3. С. 72-75].
Для решения этой проблемы были разработаны методы, преобразующие произносимую, осмысленную строку произвольной длины – пароль, в указанный ключ заранее заданной длины. В подавляющем большинстве случаев для этой операции используются так называемые хеш-функции (от англ. hashing – мелкая нарезка и перемешивание). Хеш-функцией называется такое математическое или алгоритмическое преобразование заданного блока данных, которое обладает следующими свойствами (иногда хеш-функцию называют дайджестом сообщений – MD):
- хеш-функция имеет бесконечную область определения,
- хеш-функция имеет конечную область значений,
- она необратима,
- изменение входного потока информации на один бит меняет около половины всех бит выходного потока, то есть результата хеш-функции.
Эти свойства позволяют подавать на вход хеш-функции пароли, то есть текстовые строки произвольной длины на любом национальном языке и, ограничив область значений функции диапазоном 0..2N-1, где N – длина ключа в битах, получать на выходе достаточно равномерно распределенные по области значения блоки информации – ключи.
Нетрудно заметить, что требования, подобные 3 и 4 пунктам требований к хеш-функции, выполняют блочные шифры. Это указывает на один из возможных путей реализации стойких хеш-функций – проведение блочных криптопреобразований над материалом строки-пароля. Этот метод и используется в различных вариациях практически во всех современных криптосистемах. Материал строки-пароля многократно последовательно используется в качестве ключа для шифрования некоторого заранее известного блока данных – на выходе получается зашифрованный блок информации, однозначно зависящий только от пароля и при этом имеющий достаточно хорошие статистические характеристики. Такой блок или несколько таких блоков и используются в качестве ключа для дальнейших криптопреобразований [7. С. 82].
Характер применения блочного шифра для хеширования определяется отношением размера блока используемого криптоалгоритма и разрядности требуемого хеш-результата.
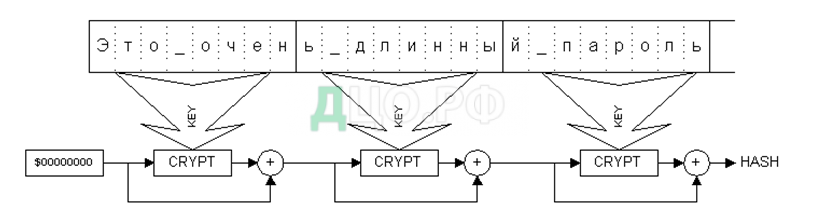
Если указанные выше величины совпадают, то используется схема одноцепочечного блочного шифрования. Первоначальное значение хеш-результата H0 устанавливается равным 0, вся строка-пароль разбивается на блоки байт, равные по длине ключу используемого для хеширования блочного шифра, затем производятся преобразования по реккурентной формуле:
Hj=Hj-1 XOR EnCrypt(Hj-1,PSWj),
где EnCrypt(X,Key) – используемый блочный шифр (рис.14).
Последнее значение Hk используется в качестве искомого результата.
В том случае, когда длина ключа ровно в два раза превосходит длину блока, а подобная зависимость довольно часто встречается в блочных шифрах, используется схема, напоминающая сеть Фейштеля. Характерным недостатком и приведенной выше формулы, и хеш-функции, основанной на сети Фейштеля, является большая ресурсоемкость в отношении пароля. Для проведения только одного преобразования, например, блочным шифром с ключом длиной 128 бит используется 16 байт строки-пароля, а сама длина пароля редко превышает 32 символа. Следовательно, при вычислении хеш-функции над паролем будут произведено максимум 2 «полноценных» криптопреобразования [11. С. 212-215].
Решение этой проблемы можно достичь двумя путями: 1) предварительно «размножить» строку-пароль, например, записав ее многократно последовательно до достижения длины, скажем, в 256 символов; 2) модифицировать схему использования криптоалгоритма так, чтобы материал строки-пароля «медленнее» тратился при вычислении ключа.
По второму пути пошли исследователи Девис и Майер, предложившие алгоритм также на основе блочного шифра, но использующий материал строки-пароля многократно и небольшими порциями [26. С. 25-35]. В нем просматриваются элементы обеих приведенных выше схем, но криптостойкость этого алгоритма подтверждена многочисленными реализациями в различных криптосистемах. Алгоритм получил название «Tandem DM» (рис.15):
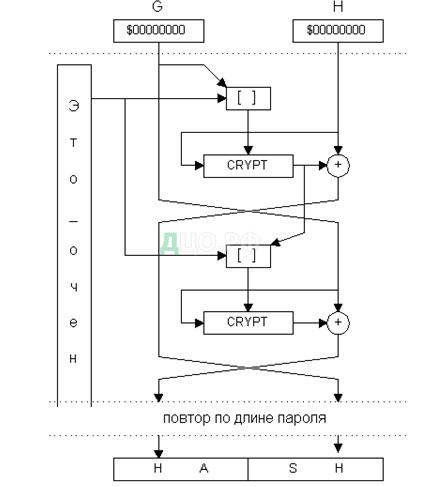
G0=0; H0=0 ;
FOR J = 1 TO N DO
BEGIN
TMP=EnCrypt(H,[G,PSWj]); H’=H XOR TMP;
TMP=EnCrypt(G,[PSWj,TMP]); G’=G XOR TMP;
END;
KEY= [Gk,Hk]
Квадратными скобками (X16=[A8,B8]) здесь обозначено простое объединение (склеивание) двух блоков информации равной величины в один – удвоенной разрядности. А в качестве процедуры EnCrypt(X,Key) опять может быть выбран любой стойкий блочный шифр. Как видно из формул, данный алгоритм ориентирован на то, что длина ключа двукратно превышает размер блока криптоалгоритма. А характерной особенностью схемы является тот факт, что строка пароля считывается блоками по половине длины ключа, и каждый блок используется в создании хеш-результата дважды. Таким образом, при длине пароля в 20 символов и необходимости создания 128 битного ключа внутренний цикл хеш-функции повторится 3 раза.
Хэш-функции прежде всего используются для обнаружения модификации сообщения (то есть для электронной подписи). В табл. 10 приведены типы хеш-функций, распространенные в настоящее время [4. С. 26].
Табл. 10. Распространенные хеш-функции
| Тип | Описание |
| MD2 | Самая медленная, оптимизирована для 8-битовых машин |
| MD4 | Самая быстрая, оптимизирована для 32-битных машин
Не так давно взломана |
| MD5 | Наиболее распространенная из семейства MD-функций.
Похожа на MD4, но средства повышения безопасности делают ее на 33% медленнее, чем MD4 Обеспечивает целостность данных Считается безопасной |
| SHA (Secure Hash Algorithm) |
Создает 160-битное значение хэш-функции из исходных данных переменного размера.
Предложена NIST и принята правительством США как стандарт Предназначена для использования в стандарте DSS |
1.10 Управление криптографическими ключами
Помимо выбора подходящей для конкретной информационной системы средств криптографической защиты информации, важной проблемой является управление ключами. Как бы ни была сложна и надежна сама криптосистема, она основана на использовании ключей. Если для обеспечения конфиденциального обмена информацией между двумя пользователями процесс обмена ключами тривиален, то в информационной системе, где количество пользователей составляет сотни и тысячи, управление ключами – серьезная проблема.
1.10.1 Симметричная методология
В этой методологии и для шифрования, и для расшифрования отправителем и получателем применяется один и тот же ключ, об использовании которого они договорились до начала взаимодействия. Если ключ не был скомпрометирован, то при расшифровании автоматически выполняется аутентификация отправителя, так как только отправитель имеет ключ, с помощью которого можно зашифровать информацию, и только получатель имеет ключ, с помощью которого можно расшифровать информацию. Так как отправитель и получатель — единственные люди, которые знают этот симметричный ключ, при компрометации ключа будет скомпрометировано только взаимодействие этих двух пользователей. Проблемой, которая будет актуальна и для других криптосистем, является вопрос о том, как безопасно распространять симметричные (секретные) ключи [11. С. 96-105].
Алгоритмы симметричного шифрования используют ключи не очень большой длины и могут быстро шифровать большие объемы данных.
Порядок использования систем с симметричными ключами:
- Безопасно создается, распространяется и сохраняется симметричный секретный ключ.
- Отправитель создает электронную подпись с помощью расчета хэш-функции для текста и присоединения полученной строки к тексту.
- Отправитель использует быстрый симметричный алгоритм шифрования/ расшифрования вместе с секретным симметричным ключом к полученному пакету (тексту вместе с присоединенной электронной подписью) для получения зашифрованного текста. Неявно таким образом производится аутентификация, так как только отправитель знает симметричный секретный ключ и может зашифровать этот пакет. Только получатель знает симметричный секретный ключ и может расшифровать этот пакет.
- Отправитель передает зашифрованный текст. Симметричный секретный ключ никогда не передается по незащищенным каналам связи.
- Получатель использует тот же самый симметричный алгоритм шифрования/расшифрования вместе с тем же самым симметричным ключом (который уже есть у получателя) к зашифрованному тексту для восстановления исходного текста и электронной подписи. Его успешное восстановление аутентифицирует кого-то, кто знает секретный ключ.
- Получатель отделяет электронную подпись от текста.
- Получатель создает другую электронную подпись с помощью расчета хэш-функции для полученного текста.
- Получатель сравнивает две этих электронных подписи для проверки целостности сообщения (отсутствия его искажения)
Доступными сегодня средствами, в которых используется симметричная методология, являются:
- Kerberos, который был разработан для аутентификации доступа к ресурсам в сети, а не для верификации данных. Он использует центральную базу данных, в которой хранятся копии секретных ключей всех пользователей.
- Сети банкоматов (ATM Banking Networks). Эти системы являются оригинальными разработками владеющих ими банков и не продаются. В них также используются симметричные методологии.
1.10.2 Асимметричная методология
В этой методологии ключи для шифрования и расшифрования разные, хотя и создаются вместе. Один ключ делается известным всем, а другой держится в тайне. Хотя можно шифровать и расшифровывать обоими ключами, данные, зашифрованные одним ключом, могут быть расшифрованы только другим ключом [6. С. 34-39].
Все асимметричные криптосистемы являются объектом атак путем прямого перебора ключей, и поэтому в них должны использоваться гораздо более длинные ключи, чем те, которые используются в симметричных криптосистемах, для обеспечения эквивалентного уровня защиты. Это сразу же сказывается на вычислительных ресурсах, требуемых для шифрования, хотя алгоритмы шифрования на эллиптических кривых могут смягчить эту проблему.
В табл. 11 приведены данные об эквивалентных длинах симметричного и открытого ключей
Табл. 11. Длина симметричного и открытого ключей
| Длина симметричного ключа | Длина открытого ключа |
| 56 бит | 384 бит |
| 64 бита | 512 бит |
| 80 бит | 768 бит |
| 112 бит | 1792 бита |
| 128 бит | 2304 бита |
Для того чтобы избежать низкой скорости алгоритмов асимметричного шифрования, генерируется временный симметричный ключ для каждого сообщения и только он шифруется асимметричными алгоритмами. Само сообщение шифруется с использованием этого временного сеансового ключа и алгоритма шифрования/расшифрования. Затем этот сеансовый ключ шифруется с помощью открытого асимметричного ключа получателя и асимметричного алгоритма шифрования. После этого этот зашифрованный сеансовый ключ вместе с зашифрованным сообщением передается получателю. Получатель использует тот же самый асимметричный алгоритм шифрования и свой секретный ключ для расшифрования сеансового ключа, а полученный сеансовый ключ используется для расшифровки самого сообщения.
В асимметричных криптосистемах важно, чтобы сеансовые и асимметричные ключи были сопоставимы в отношении уровня безопасности, который они обеспечивают. Если используется короткий сеансовый ключ ( например, 40-битовый DES), то не имеет значения, насколько велики асимметричные ключи. Хакеры будут атаковать не их, а сеансовые ключи. Асимметричные открытые ключи уязвимы к атакам прямым перебором отчасти из-за того, что их тяжело заменить. Если атакующий узнает секретный асимметричный ключ, то будет скомпрометирован не только текущее, но и все последующие взаимодействия между отправителем и получателем [5. С. 45-47].
Порядок использования систем с асимметричными ключами:
- Безопасно создаются и распространяются асимметричные открытые и секретные ключи. Секретный асимметричный ключ передается его владельцу. Открытый асимметричный ключ хранится в базе данных X.500 и администрируется центром выдачи сертификатов (по-английски — Certification Authority или CA). Подразумевается, что пользователи должны верить, что в такой системе производится безопасное создание, распределение и администрирование ключами. Более того, если создатель ключей и лицо или система, администрирующие их, не одно и то же, то конечный пользователь должен верить, что создатель ключей на самом деле уничтожил их копию.
- Создается электронная подпись текста с помощью вычисления его хэш-функции. Полученное значение шифруется с использованием асимметричного секретного ключа отправителя, а затем полученная строка символов добавляется к передаваемому тексту (только отправитель может создать электронную подпись).
- Создается секретный симметричный ключ, который будет использоваться для шифрования только этого сообщения или сеанса взаимодействия (сеансовый ключ), затем при помощи симметричного алгоритма шифрования/расшифрования и этого ключа шифруется исходный текст вместе с добавленной к нему электронной подписью – получается зашифрованный текст (шифр-текст).
- Теперь нужно решить проблему с передачей сеансового ключа получателю сообщения.
- Отправитель должен иметь асимметричный открытый ключ центра выдачи сертификатов (CA). Перехват незашифрованных запросов на получение этого открытого ключа является распространенной формой атаки. Может существовать целая система сертификатов, подтверждающих подлинность открытого ключа CA. Стандарт X.509 описывает ряд методов для получения пользователями открытых ключей CA, но ни один из них не может полностью защитить от подмены открытого ключа CA, что наглядно доказывает, что нет такой системы, в которой можно было бы гарантировать подлинность открытого ключа CA.
- Отправитель запрашивает у CA асимметричный открытый ключ получателя сообщения. Этот процесс уязвим к атаке, в ходе которой атакующий вмешивается во взаимодействие между отправителем и получателем и может модифицировать трафик, передаваемый между ними. Поэтому открытый асимметричный ключ получателя «подписывается» CA. Это означает, что CA использовал свой асимметричный секретный ключ для шифрования асимметричного открытого ключа получателя. Только CA знает асимметричный секретный ключ CA, поэтому есть гарантии того, что открытый асимметричный ключ получателя получен именно от CA.
- После получения асимметричный открытый ключ получателя расшифровывается с помощью асимметричного открытого ключа CA и алгоритма асимметричного шифрования/расшифрования. Естественно, предполагается, что CA не был скомпрометирован. Если же он оказывается скомпрометированным, то это выводит из строя всю сеть его пользователей. Поэтому можно и самому зашифровать открытые ключи других пользователей, но где уверенность в том, что они не скомпрометированы?
- Теперь шифруется сеансовый ключ с использованием асимметричного алгоритма шифрования/расшифрования и асимметричного ключа получателя (полученного от CA и расшифрованного).
- Зашифрованный сеансовый ключ присоединяется к зашифрованному тексту (который включает в себя также добавленную ранее электронную подпись).
- Весь полученный пакет данных (зашифрованный текст, в который входит помимо исходного текста его электронная подпись, и зашифрованный сеансовый ключ) передается получателю. Так как зашифрованный сеансовый ключ передается по незащищенной сети, он является очевидным объектом различных атак.
- Получатель выделяет зашифрованный сеансовый ключ из полученного пакета.
- Теперь получателю нужно решить проблему с расшифровкой сеансового ключа.
- Получатель должен иметь асимметричный открытый ключ центра выдачи сертификатов (CA).
- Используя свой секретный асимметричный ключ и тот же самый асимметричный алгоритм шифрования получатель расшифровывает сеансовый ключ.
- Получатель применяет тот же самый симметричный алгоритм шифрования/расшифрования и расшифрованный симметричный (сеансовый) ключ к зашифрованному тексту и получает исходный текст вместе с электронной подписью.
- Получатель отделяет электронную подпись от исходного текста.
- Получатель запрашивает у CA асимметричный открытый ключ отправителя.
- Как только этот ключ получен, получатель расшифровывает его с помощью открытого ключа CA и соответствующего асимметричного алгоритма шифрования/расшифрования.
- Затем расшифровывается хэш-функция текста с использованием открытого ключа отправителя и асимметричного алгоритма шифрования/расшифрования.
- Повторно вычисляется хэш-функция полученного исходного текста.
- Две эти хэш-функции сравниваются для проверки того, что текст не был изменен.
Итак, все криптосистемы делятся на симметричные и асимметричные. Симметричные криптосистемы используют секретный ключ, который используется как для шифрования текста, так и для его расшифрования. Чем отличаются асимметричные криптосистемы, которые используют 2 ключа – открытый и закрытый. Открытый ключ нужен для шифрования текста, а закрытый – для его расшифрования. В настоящее время к наиболее популярным симметричным криптосистемам относят блочные шифры, которые выделяются достаточной криптостойкостью и простотой процедур шифрования и расшифрования, а также генерацией ключа. Не смотря на свою простоту блочные шифры имеют высокую скорость шифрования/расшифрования файла, а также высокую гарантированную стойкость.
Блочные шифры базируются на сетях Фейштеля, которые разбивают шифруемый текст на блоки, перемешают их, используя «исключающее ИЛИ» и циклические сдвиги, а также количество раундов шифрования. Чем больше раундов применимо к блоку, тем более надежен и криптостоик он.
Одним из самых распространенных алгоритмов блочного шифрования является DES (Data Encryption Standard), который получил достаточно широкое распространение в свое время. Однако, со временем, на его место пришел наиболее усовершенствованный AES (Advanced Encryption Standard), который стал де-факто мировым криптостандартом на ближайшие 10-20 лет. Наиболее яркие его представители это MARS, Serpent, TwoFish, Rijndael и RC6, а также российский представитель стандарт шифрования данных – ГОСТ 28147-89.
Асимметричные криптосистемы не столь обширны как симметричные, т.к. они сложны и менее производительны. Яркие его представители – это система RSA, криптосистема Эль-Гамаля и криптосистема на основе эллиптических уравнений и другие.
Таким образом, симметричные криптосистемы обладают более быстрой скоростью шифрования данных, чем асимметричные, которые часто используют только для шифрования небольших объемов информации, например для рассылки классических секретных ключей или в алгоритмах цифровой подписи, а основную часть пересылаемой информации шифруют с помощью симметричных алгоритмов.
Наиболее устойчивыми к взлому алгоритмами шифрования являются IDEA, CAST128, BlowFish, TwoFish, MARS и ГОСТ.
Одна из важнейших задач обеспечения безопасности является идентификация и аутентификация пользователей, которые заключаются, например, в вводе логина и пароля. Аутентификация требуется в персональных идентификационных номерах (PIN), магнитных карты, смарт-картах. Самая опасная угроза аутентификации возникает в том случае, когда нарушитель выдает себя за какую-либо другую сторону, обычно обладающими существенными привилегиями в системе, поэтому одной из основных задач является разграничение доступа к ресурсам, когда при привилегированном доступе необходимо убедиться в идентичности пользователей.
Для защиты электронной почты от несанкционированного прочтения и ее изменения применяются электронно-цифровые подписи, которые подтверждают своего отправителя. В электронно-цифровой подписи при помощи симметричных криптосистем участвуют отправители А, В, а также независимый доверенный арбитр Х, который используя ключи обоих отправителей, расшифровывает и зашифровывает сообщение и отсылает его назад отправителям. Однако на практике симметричные криптосистемы для выработки подписи не используются, поскольку требуют дорогостоящих и громоздких мероприятий по поддержанию достаточного уровня достоверности передаваемых данных. Поэтому в настоящее время используются менее замысловатые асимметричные криптосистемы. В них абоненты используют пару взаимосвязанных ключей – открытый и секретный. Отправитель зашифровывает сообщение открытым ключом, а получатель расшифровывает его используя только известный ему – секретный ключ.
Метод хеширования паролей позволяет преобразовать длинный пароль в ключ заранее заданной длины. В подавляющем большинстве случаев для этой операции используются так называемые хеш-функции. На входе хеш-функции задаются пароли, то есть текстовые строки произвольной длины в битах, а на выходе достаточно равномерно распределенные по области значения блоки информации – ключи.
Управление криптографическими ключами является серьезной проблемой когда количество пользователей составляет сотни и тысячи. Как было сказано выше, алгоритмы симметричного шифрования используют одинаковые ключи для шифрования и расшифрования данных. Доступными сегодня средствами, в которых используется симметричная методология, являются Kerberos, который был разработан для аутентификации доступа к ресурсам в сети и сети банкоматов (ATM Banking Networks), в которых используются симметричные методологии.
В асимметричном шифрования для того чтобы избежать низкой скорости алгоритмов, генерируется временный симметричный ключ для каждого сообщения и только он шифруется асимметричными алгоритмами. Само сообщение шифруется с использованием этого временного сеансового ключа и алгоритма шифрования/расшифрования. Затем этот сеансовый ключ шифруется с помощью открытого асимметричного ключа получателя и асимметричного алгоритма шифрования. После этого этот зашифрованный сеансовый ключ вместе с зашифрованным сообщением передается получателю. Получатель использует тот же самый асимметричный алгоритм шифрования и свой секретный ключ для расшифровки сеансового ключа, а полученный сеансовый ключ используется для расшифровки самого сообщения.
