Введение

Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического уравнения. Оказалось, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами – тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный корень.

На множестве рациональных чисел разрешимы алгебраические уравнения первой степени, т.е. уравнения вида A•X+B=0. Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.

Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них – уравнение X²+1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.

Комплексными числами называют выражения вида A+B•i, где A и B –действительные числа, а i – некоторый символ, такой что i²= –1. Число A называется действительной частью комплексного числа A+B•i, а число B – его мнимой частью. Число i называется мнимой единицей.

Два комплексных числа считаются равными, если у них равны вещественные и мнимые части:

Z1 = Z2 ↔ A1 = A2 ˄ B1 = B2

Но вот операции типа «больше» и «меньше» для комплексных чисел не имеют смысла, то есть бессмысленно писать Z1 < Z2 или Z1 > Z2. Совершенно непонятно, что больше 2 + 3i или 3 + 2i, т. к. комплексные числа не упорядочены. Исходя из этого, для выполнения поставленной задачи, а именно – сортировки комплексных чисел, необходимо выработать условный критерий, по которому можно было бы отсортировать набор чисел.

Комплексное число также можно изображать на плоскости радиус-вектором. Длина радиус-вектора, изображающего комплексное число Z = A + Bi, называется модулем этого комплексного числа и определяется по формуле:

|Z| = |A + Bi| = 

В рамках работы необходимо создать библиотеку для работы с комплексными числами на языке C++.

Цели и задачи работы:

1. Создание структуры данных, представляющей комплексное число, состоящего из вещественной и мнимой частей.

2. Реализация основных математических операций над комплексными числами, таких как сложение, умножение, деление.

3. Реализация функций, позволяющих получить действительную и мнимую части комплексного числа.

4. Разработка методов для удобного вывода комплексного числа.

5. Создание возможности для изменения комплексного числа.

6. Обеспечение возможности сравнения комплексных чисел.

7. Проверка всех реализованных функций и методов на корректность и оптимизацию кода для достижения высокой производительности.

В результате работы над библиотекой «Комплексные числа» на языке C++ будет создан набор функций и методов для работы с комплексными числами, а также примеры использования этих функций. Это поможет разработчикам использовать комплексные числа в своих программах с минимальными усилиями и обеспечит возможность работать с ними эффективно и удобно.

1. Проектирование библиотеки «Комплексные числа»

1.1. Определение функций в разрабатываемой библиотеке

1.2. Постановка задачи на разработку библиотеки «Комплексные числа»

В рамках работы требуется разработать проект, который позволяет ввести с клавиатуры количество комплексных чисел (задать размер массива), создать и заполнить с клавиатуры массив комплексных чисел заданного размера, затем многократно выбрать одну из нескольких операций над одним или более комплексным числом: изменить комплексное число по номеру в массиве, сравнить два комплексных числа на равенство, сложить два или более комплексных числа, умножить два или более комплексных числа, разделить два или более комплексных числа. Вывод результата выбранного действия осуществляется в консоль программы.

1.3. Выбор инструментария для разработки библиотеки «Комплексные числа»

Выбор языка программирования и среды разработки для разработки библиотеки «Комплексные числа» зависит от предпочтений разработчика, пользователя и требований проекта.

Одним из популярных языков программирования для разработки библиотеки может быть Python. Python является простым и элегантным языком программирования, который имеет множество библиотек и инструментов для работы с математическими вычислениями. Можно использовать интегрированную среду разработки Python, такую как PyCharm или Visual Studio Code, чтобы начать разрабатывать комплексные числа.

Другие высокоуровневые языки, такие как C++, Java или JavaScript также можно использовать для разработки библиотеки. В таком случае потребуется выбрать соответствующую среду разработки для выбранного языка (например, Visual Studio для C++ или IntelliJ IDEA для Java).

Кроме того, можно использовать MATLAB или Octave для разработки библиотеки комплексных чисел. MATLAB и Octave имеют встроенную поддержку для работы с комплексными числами и предлагают множество инструментов для численных вычислений.

Одной из основных причин выбора языка программирования C++ является его высокая производительность. C++ предоставляет возможность эффективного использования ресурсов компьютера, таких как память и процессорное время. Это особенно важно при разработке приложений, требующих больших вычислительных мощностей, например, в области научных и инженерных вычислений.

Кроме того, C++ является достаточно низкоуровневым языком программирования, что дает разработчикам полный контроль над выполнением программы. Это позволяет оптимизировать код и создавать более эффективные и производительные приложения.

Другой важной причиной выбора C++ является его широкая поддержка в индустрии. C++ использовался и продолжает использоваться в различных областях программной инженерии, включая разработку системного и прикладного программного обеспечения, игр, встроенных и реального времени приложений.

Также C++ обладает мощными средствами объектно-ориентированного программирования (ООП) и обобщенного программирования, что делает его гибким инструментом для разработки сложных приложений. Это позволяет создавать модульный и переносимый код, упрощать разработку и обслуживание программного обеспечения.

Наконец, C++ имеет большую базу пользователей и разработчиков, что обеспечивает доступ к обширному сообществу, библиотекам и инструментам, которые могут упростить разработку и расширить функциональность разрабатываемых приложений.

Все эти факторы делают C++ привлекательным выбором для разработки сложных программных проектов, требующих высокой производительности, гибкости и возможности оптимизации кода.

Выбор среды программирования Visual Studio Community обосновывается рядом преимуществ:

1. Бесплатность: Visual Studio Community является бесплатной версией среды Visual Studio, предлагающей множество возможностей для разработки.

2. Богатый функционал: Visual Studio Community обладает широким набором инструментов и функций для разработки, включая интегрированную систему контроля версий, отладчик, редактор кода с подсветкой синтаксиса и автозаполнением, а также множество встроенных шаблонов и библиотек.

3. Поддержка различных языков программирования: Visual Studio Community позволяет разрабатывать приложения на различных языках программирования, включая C++, C#, Visual Basic, Python и др.

4. Экосистема разработчиков: Visual Studio Community интегрируется с экосистемой Microsoft, что обеспечивает доступ к большому количеству дополнительных инструментов, библиотек и ресурсов для разработки.

5. Простота использования: Visual Studio Community обладает интуитивным интерфейсом и простыми инструментами, что делает ее подходящей для новичков и опытных разработчиков.

6. Поддержка платформы .NET: Visual Studio Community полностью интегрирована с платформой .NET, позволяя разрабатывать приложения для операционных систем Windows, iOS, Android и Web.

7. Регулярные обновления: Visual Studio Community регулярно выпускает обновления для исправления ошибок, добавления новых функций и поддержки последних технологий.

В целом, выбор Visual Studio Community обосновывается своей бесплатностью, обширным функционалом, поддержкой различных языков программирования, простотой использования и интеграцией с экосистемой разработчиков Microsoft. Это делает ее широко используемой и популярной средой программирования.

1.4. Структура библиотеки

Программа выполнена с использованием принципов ООП.

Для описания комплексного числа необходимо описать базовый класс Complex, содержащий поля re и im для описания действительной и мнимой частей соответственно. В классе должны быть определены конструкторы по умолчанию и с параметрами.

Исходный код базового класса приведен в листинге 1.

Листинг 1. Класс комплексного числа

class Complex

protected:

  double re, im;

public:

  Complex();                                                                                                                                                     

  Complex(double);                                                                                                                         

  Complex(double, double);

  Complex(const Complex&);

  ~Complex() {};                                           

Для реализации основных операций над комплексными числами необходимо описать производный класс ExtendedComplex, в котором определить перегрузки операторов ввода и вывода, сравнения на равенство, а также операции суммирования, умножения и деления пары комплексных чисел.

2. Реализация библиотеки «Комплексные числа»

2.1. Реализация алгоритмов

Основные действия по работе с комплексными числами реализованы в виде перегруженных операторов класса.

Алгоритм главной программы был формализован в виде блок-схемы, которая приведена на рисунке 1.

 

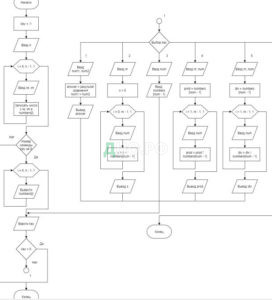
Рисунок 1. Блок-схема главного алгоритма программы

Блок-схема была построена средствами онлайн-сервиса draw.io и сохранена формате А4 в виде изображения с расширением *.jpg.

Реализация данного алгоритма выполнена в виде программ, написанных на языке C++ среди Visual Studio 2019. Программы написаны хорошим стилем программирования, читабельны: блоки программы оформлены отступами, операторы снабжаются комментариями.

Листинг программы приведен в Приложении 1.

Схема классов программы представлена на рисунке 2.

Рисунок 2. Состав классов программы (публичное наследование)

2.2. Реализация тестовой программы

Для понимания сути разрабатываемого приложения и формирования алгоритма необходимо описать контрольные тестовые примеры, позволяющие решить поставленную задачу.

Пусть имеется следующий набор комплексных чисел:

c1 = 3 – 5i

c2 = 2 – 7i

c3 = –1 – i

c4 = 1 + i

И для тестирования необходимо проверить основные арифметические операции над комплексными числами. Для этого выполнить следующие действия:

Сложить три числа: с4 и с2, а затем сложить результат с с4.

с4 + с2 = (1 + i) + (2 – 7i) = (1+ 2) + (i – 7i) = 3 – 6i.

c4 + c2 + c4 = (3 – 6i) + (1 + i) = 4 – 5i.

Ответ: 4 – 5i – корректно.

Умножить два числа: с3 и с4.

с3 + с4 = (–1 – i) * (1 + i) = (–1) * 1 + (–i) * 1 + (–1) * i + (–i) * i = –1 – i – i – i² = –1 – 2i + 1 = – 2i.

Ответ: –2i – корректно.

Разделить два числа: с1 разделить на с2.

c1 / c2 = (3 – 5i) / (2 – 7i) = (3 * 2 + (–5) * (–7)) / (2² + (–7)²) + ((–5 * 2 – 3 * (–7)) / (2² + (–7)²))i = (6 + 35) / (4 + 49) + ((–10 + 21) / (4 + 49))i = 41 / 53 + (11 / 53)i = 0,77358 + 0,207547i.

Ответ: 0,77358 + 0,207547i – корректно.

В главной программе необходимо выполнить тестирование на описанных контрольных примерах.

2.3. Тестирование библиотеки

Тестирование на контрольных примерах – это процесс проверки работы программного обеспечения на базе уже известных входных данных и ожидаемых результатов.

Для проведения тестирования на контрольных примерах необходимо иметь набор тестовых случаев, которые представляют испытания для программы. Входные данные должны быть известными и корректными, а ожидаемые результаты должны быть известны заранее.

Целью тестирования на контрольных примерах является выявление ошибок или несоответствий между ожидаемыми и фактическими результатами работы программы. Это позволяет проверить правильность функционирования программного обеспечения, его соответствие спецификации и требованиям.

Преимуществом тестирования на контрольных примерах является возможность систематической проверки работоспособности программы и обнаружения возможных ошибок. Однако оно не позволяет полностью охватить все возможные сценарии использования программы и проверить ее на нестандартных или крайних случаях.

Тестирование на контрольных примерах следует проводить в сочетании с другими методами тестирования, такими как тестирование на граничных значениях, тестирование случайных значений, тестирование на мутацию и др. Такой подход позволяет обеспечить более полное и надежное тестирование программного обеспечения.

Тестирование в виде скриншотов консоли является одним из способов представления результатов тестирования. Этот формат позволяет показать все шаги тестирования и соответствующие результаты. Преимущества использования скриншотов консоли в тестировании:

1. Легкость понимания: скриншоты консоли четко показывают шаги тестирования и результаты. Это позволяет быстро оценить состояние системы и принять соответствующие меры.

2. Доказательство ошибок: скриншоты консоли служат доказательством найденных ошибок. Это может быть полезно при обсуждении и исправлении ошибок с разработчиками или другими участниками проекта.

3. Воспроизводимость: скриншоты консоли также позволяют воспроизвести тестирование. Путем повторного выполнения тех же самых действий, показанных на скриншотах, можно убедиться в правильности результатов.

В целом, использование скриншотов консоли является одним из способов представления результатов тестирования, который может быть полезным в определенных случаях, но не является универсальным методом и может иметь свои ограничения.

Тестирование программы проведено путем сравнения результатов е работы с контрольными примерами, описанными ранее. Скриншот решения (рисунок 3) показывает, что результаты совпадают.

Рисунок 3. Результаты тестирования программы

Пользовательский интерфейс программы отображает необходимые шаги, которые пользователь/оператор должен предпринять для того, чтобы корректно решить поставленную задачу.

Таким образом, в разработан алгоритм и соответствующая ему программа, в которой реализуются стандартных операции над комплексными числами в алгебраической форме z=A+iB. i – комплексная 1=√−1. Созданы соответствующие классы, реализована перегрузка операторов для сложения, умножения и деления комплексных чисел, сравнения их на равенство, ввода с клавиатуры и вывода на экран.

Программа написана на языке C++ в интегрированной среде разработки Visual Studio 2019 Community и функционирует в операционной системе Windows 10.

Установка программы не требуется. Для вызова программы необходимо запустить файл «ComplexProject.exe».

Пользователь при запуске программы вводит натуральное число n (количество комплексных чисел) с консоли. Затем пользователь вводит n комплексных чисел с клавиатуры, задавая действительную и мнимую части для каждого числа. Программа выведет на экран все комплексные числа в нужном формате.

После ввода необходимо выбрать операцию (номер команды меню от 0 до 5 в предложенном списке команд). Программа выведет на экран результат выбранной операции над одним или несколькими комплексными числами.

Заключение

В данной работе была создана программа, позволяющая выполнить основные операции с комплексными числами. Исследование состояло из нескольких этапов.

Для понимания сути задачи и для формирования алгоритма было составлено несколько контрольных примеров: были подобраны комплексные числа и протестированы основные операции с ними.

На основе анализа контрольного примера была продумана стратегия решения задачи и те алгоритмические приёмы, которые можно применить для её выполнения.

Выбранная стратегия решения позволила разбить основные структурные единицы на классы, а алгоритмы – на отдельные методы, и реализовать преимущества объектно-ориентированного подхода.

Разработанный и формализованный в виде блок-схемы алгоритм основной программы позволил записать код на языке С++.

Завершающим этапом исследования было тестирование программы на основе контрольных примеров. Оно прошло успешно и продемонстрировало корректность и полноту разработанного программного комплекса.

Таким образом, все поставленные в итоговой работе задачи были выполнены. Программа отлажена и может применяться на практике.

Список использованных источников

1. Петрова Н.К. Конспект лекций «Программирование на С++». Электронный документ https://lms.kgeu.ru/course/view.php?id=2594.

2. Павловская Т. А. «Программирование на языке C++»: учебник для вузов / Национальный Открытый Университет «ИНТУИТ», 2016. Электронный документ https://e.lanbook.com/book/100409?category=1557.

3. Курсовая работа по дисциплине «Алгоритмизация и программирование»: методические указания / сост. Петрова Н.К., С.М. Куценко. – Казань: Казан. гос. энерг. ун-т, 2019. – 51 с.

4. Сидорина, Т. Самоучитель Microsoft Visual Studio C++ и MFC / Т. Сидорина. – М.: БХВ-Петербург, 2014. – 848 c.