Разработка кодовой конструкции, позволяющей исправлять стертые слова внутреннего кода при использовании каскадного кода. Часть 3.

---

Страницы:   1   2   3   4   5

---

6.2. Ускоренный алгоритм Берлекэмпа – Месси

Ускоренный алгоритм обосновывается следующим образом. На начальных итерациях алгоритм Берлекэмпа—Месси в частотной области содержит умеренное число умножений порядка степени многочлена L (х). Но степень многочлена L (х) возрастает до существенной доли длины n, и таким образом, среднее число умножений на итерацию имеет порядок n. Преимущества ускоренного алгоритма связаны попросту с тем, что на ранних шагах несколько итераций в частотной области выполняются одновременно. После такого пакетного выполнения нескольких итераций полученный промежуточный результат используется для модификации синдрома путем ввода в него вычисленных в этом пакете многочленов L (х) и В (х). Следующий пакет итераций начинает выполнение алгоритма Берлекэмпа—Месси, сначала используя в качестве синдрома вычисленный модифицированный синдром и полагая в начальный момент L (х) равным 1.

В перестроенном виде алгоритм Берлекэмпа—Месси основывается на двух уравнениях:

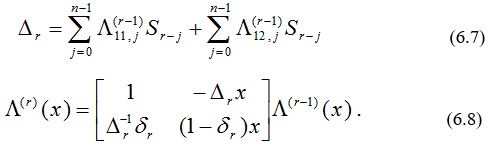
Теперь можно уменьшить число вычислений, группируя итерации в пакеты. Определим матрицу

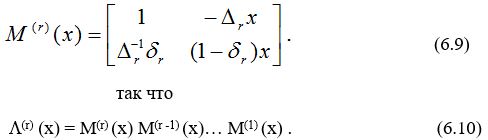
Это произведение должно вычисляться последовательно по одному члену, начиная справа, так как M^(r) (x) нельзя вычислить до тех пор, пока не вычислена L^{(r -1)} (x).

Определим следующие частичные произведения рассматриваемых матриц:

                              L^(r) (x) = L^{(r , 0)} (x)                                                     (6.11)

                              L^(r) (x) = L^{(r ,  r’)} (x) L^(r’) (x).                                   (6.12)

Определим вектор модифицированных синдромных многочленов S^(r) (x):

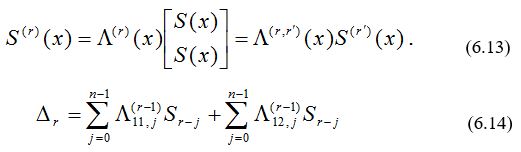
Невязка становится равной r – му члену свертки и может быть записана через многочлены :

D(x) = L₁₁^{(r –1, r’)} (x) [ L₁₁^{( r’)} (x)S(x) + L₁₂^{( r’)} (x)S(x) ] + L₂₁^{(r –1, r’)} (x) [ L₂₁^{( r’)} (x)S(x) + L₂₂^{( r’)} (x)S(x) ].         (6.15)

Стоящие в квадратных скобках многочлены являются компонентами вектора S^(r’) (x) модифицированных синдромных многочленов. Следовательно, выражение для невязки можно переписать в виде

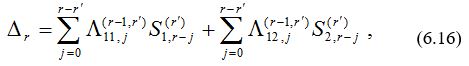
где S^(r)_{1 , j} и S^(r)_{2 , j} обозначают соответственно j-е коэффициенты многочленов в первой и второй компонентах вектора S^(r) (х). Для ускорения алгоритма Берлекэмпа—Месси сформируем па­кеты по t итераций в каждом. Если t делит 2t, то обращение к каждому из 2t/t пакетов одинаково. В противном случае послед­ний пакет содержит меньше t итераций, но мы полагаем его та­ким же. Индекс r теперь пробегает значения

r = 1, 2,…, t,  t+1,…, 2t, 2t+1,…, 3t,  3t+1,…

На r-й итерации k-го пакета модифицированный алгоритм Бер­лекэмпа—Месси вычисляет L^{(r , r’)} (х) согласно равенству

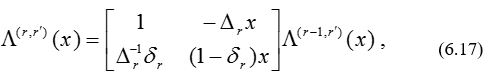
где r’ = kt , а  D_r  вычисляется по формуле

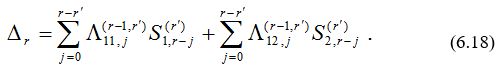
В конце k-го пакета, когда r равно (k + 1)t, матрица локаторов ошибок и вектор модифицированных синдромных многочленов даются соответственно равенствами

L^(r) (x) = L^{(r, r’)} (x) L^(r’) (x)                                (6.19)

S^(r) (x) = L^{(r, r’)} (x) S^(r’) (x) ,                               (6.20)

где r’ = kt  и  r = (k + 1)t . Теперь ускоренный алгоритм готов начать (k + 1)–й пакет.

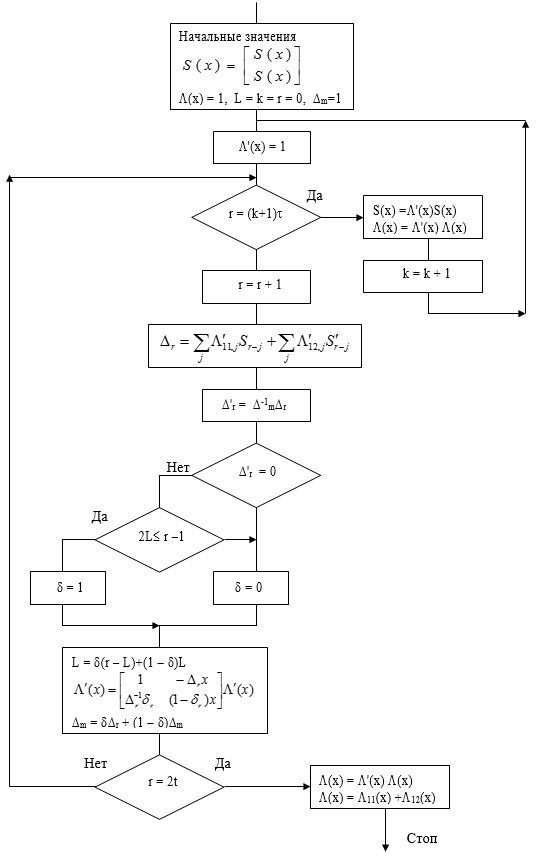
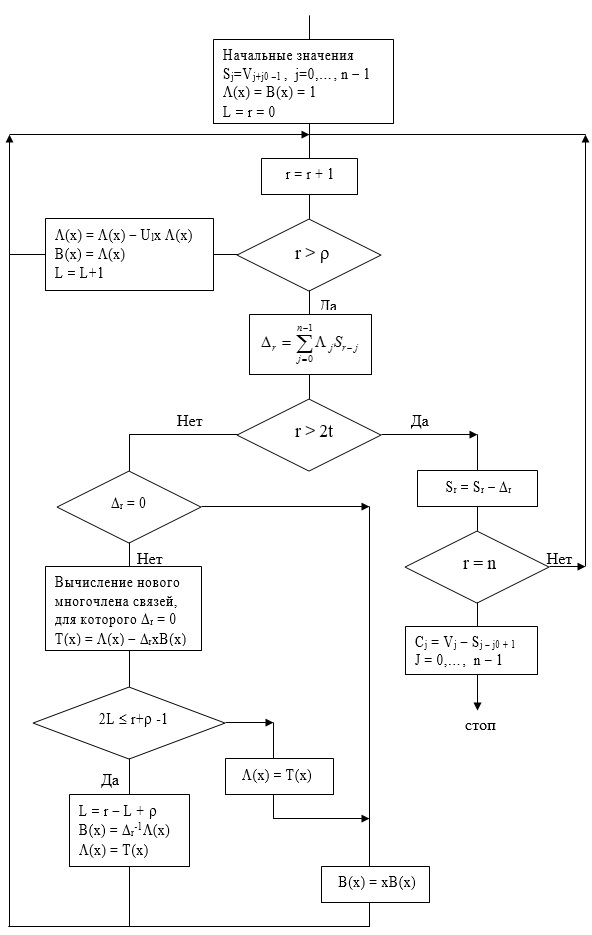
На рисунке 6.2 приведена блок-схема ускоренного алгоритма Берлекэмпа — Месси с некоторыми очевидными сокращениями. Если правая часть алгоритма выполняется так, как она выписана, то мы не получаем никакой экономии вычислений. Однако умножения многочленов в блоках эквивалентны сверткам, которые могут быть эффективно вычислены с помощью быстрого преобразо­вания Фурье и теоремы о свертке.

 

ГЛАВА 7. ИСПРАВЛЕНИЕ СТИРАНИЙ И ОШИБОК

В дипломной работе используется каскадный код, внешним кодом которого является код Рида – Соломона (255, K, D) над полем GF (2⁸), а внутренним – код Голея (24, 12, 8). В следствии чего три 8-битных символа  внешнего кода составляют два 12-битных кодовых слова внутреннего кода. При декодировании внутреннего кода могут появиться стертые кодовые слова – это слова в которых произошло четыре ошибки, и значит они не могут быть декодированы. Стертые кодовые слова внутреннего кода заменяются нулями, обозначающими стирания. Следовательно во внешнем коде появляются два стертых 8-битных символа, заполненных нулями.  В силу чего декодер внешнего кода должен исправить ошибки и восстановить стертые символы. Код с мини­мальным расстоянием d* позволяет декодировать любую конфи­гурацию, содержащую v ошибок r стираний, при условии, что

d*  ³ 2v + t + r.                                           (7.1)

Наибольшее v, удовлетворяющее этому неравенству, обозначим через t_p.

Чтобы декодировать принятое слово с r стираниями, необхо­димо найти кодовое слово, которое в нестертых позициях отли­чается от принятого слова не более чем в t_p символах. Поскольку по определению параметра t_р такое слово единственно, разыскивается любое подходящее слово. Нам нужно только найти какое либо решение, так как мы знаем, что оно лишь одно.

Один из возможных способов декодирования состоит в угадывании стертых позиций с последующим применением любой процедуры исправления ошибок. Если процедура приводит к исправ­лению не более t_p ошибок в нестертых позициях, то кодовое слово восстанавливается. Если необходимо исправлять слишком много ошибок, то делается новая попытка угадать стертые сим­волы. При этом любая подходящая для данного кода процедура исправления ошибок может быть модифицирована в процедуру исправления ошибок и стираний. Практически она подходит в тех случаях, когда число комбинаций угадываемых стертых сим­волов мало. В противном случае такая процедура проб и ошибок становится практически неприемлемой. В таких случаях восста­новление стертых символов должно осуществляться некоторым регулярным способом, входящим в алгоритм декодирования.

Класс кодов БЧХ допускает многие сильные алгоритмы декодирования. Все они могут быть обобщены на случай декодирования ошибок и стираний. Для простоты будем полагать j₀ = 1.

Пусть V_i, i = 0, …, n — 1, обозначают символы принятого вектора. Предположим, что стирания произошли в позициях i₁, …, i_p. Во всех этих позициях принятое слово содержит пробелы, которые мы сначала заполним нулями. Определим n-мерный вектор стираний, положив символы в стертых позициях рав­ными f_il , l = 1, …, r, а в остальных позициях равными нулю. Тогда

v_i = c_i  + e_i + f_i  ,    i =0, . . . , n — 1 .                               (7.2)

Пусть y — произвольный вектор, символы которого равны нулю в каждой позиции стирания и только в них. Тогда

y_i v_i = y_i (c_i  + e_i + f_i  ) = y_i c_i + y_i e_i                              (7.3)

Определим модифицированное принятое слово равенством v’_i = y_i v_i, модифицированный  вектор  ошибок  равенством  e’_i = y_i e_i  и модифицированное кодовое слово равенством c’_i = y_i c_i. (Модифицированный вектор ошибок содержит ошибки в тех же позициях, что и исходный вектор ошибок е.) Тогда последнее равенство приводится к виду

v’_i = c’_i + e’_i .                                               (7.4)

Теперь задача состоит в декодировании вектора v’ и сводится к задаче вычисления вектора е’, которую можно решить при достаточном числе компонент синдрома.

Следующий шаг построения алгоритма состоит в выборе век­тора Y. Пусть U_l = a^il для l = 1, …, r обозначают локаторы стираний. Определим многочлен локаторов стираний равенством

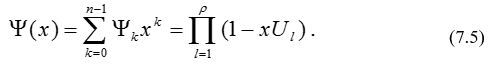
Этот многочлен специально определен так, чтобы компоненты y_i обратного преобразования вектора Y были равны нулю, как только f_i ¹ 0. Следовательно, y_i f_i = 0. В частотной области это дает

V’ = (Y * С) + Е’.                                                  (7.6)

Но вектор Y отличен от нуля только на блоке длины r + 1, а по построению кода БЧХ вектор С имеет нулевые компоненты в блоке длины 2t. Следовательно, свертка Y * С равна нулю в блоке длины 2t — r. Полагая    S’_j = V’_j, определим на этом блоке модифицированный синдром. Тогда

S’_j = (Y*V)_j + E’_j ,                                                 (7.7)

что задает достаточное число компонент синдрома для исправле­ния модифицированного вектора ошибок.

Итак, точно так же, как в случае наличия только ошибок (при условии, что их не более (2t — r)/2 ), по этим 2t — r извест­ным компонентам вектора Е’ можно найти многочлен локаторов ошибок L (х). Так как многочлен локаторов ошибок известен, можно скомбинировать его с многочленом локаторов стираний и дальнейшее декодирование проводить так же, как и в случае на­личия только ошибок. Чтобы проделать это, определим сначала многочлен локаторов ошибок и стираний:

L’ (х) = Y(х)L(x) .                                                (7.8)

Обратное преобразование Фурье вектора L’ содержит нуль в по­зиции каждой ошибки и каждого стирания. Таким образом, l_i = 0, если е_i ¹ 0 или    f_i ¹ 0. Следовательно, l_i (e_i + f_i) = 0,

L’ * (Е + F) = 0,                                                      (7.9)

и многочлен L’ отличен от нуля в блоке длины, не превышающей v + r + 1. Следовательно, используя известные компо­ненты вектора L’ и 2t известных компонент вектора Е + F, можно воспользоваться этим содержащим свертку уравнением для того, чтобы рекуррентно продолжить вектор Е + F до всех n компонент. Затем вычисляются

C_i = V_i – (E_i + F_i).                                                (7.10)

Вычисление многочлена локаторов ошибок по модифицированному значению синдрома можно выполнить с помощью алгоритма Берлекэмпа—Месси. Можно улучшить алгоритм Берлекэмпа – Месси, если скомбинировать несколько шагов. Идея алгоритма состоит в рекуррентной процедуре вычисления многочлена L(x) за 2t итераций, начиная с оценок  L⁽⁰⁾ (x) = 1 и    B⁽⁰⁾ (х)  = 1.

В случае наличия стираний в уравнении для невязки D_r ком­поненты синдрома заменяются компонентами модифицирован­ного синдрома:

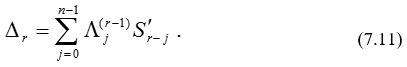
Многочлен локаторов ошибок вычисляется с помощью n итераций при начальных условиях L⁽⁰⁾ (x) = 1 и B⁽⁰⁾ (х)  = 1.

Заменим начальные условия на L⁽⁰⁾ (x) = B⁽⁰⁾ (x) = Y (x). Тогда

L^(r) (x) Y (x) = L^{(r -1)} (x) Y (x) – D_r B^{(r -1)} (x) Y (x) ,                           (7.12)

B^(r) (x) Y (x) = (1 – d_r)x B^{(r -1)} (x) Y (x) + d_r D_r^-1 L^{(r -1)} (x) Y (x) .    (7.13)

Если мы временно  определим  L’^(r) (x) = L^(r) (x) Y (x) и будем вычислять невязку D_r по формуле

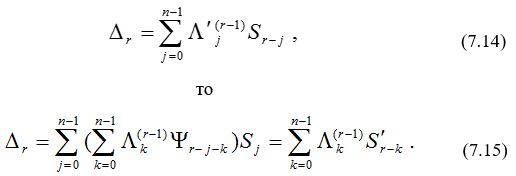
Итак, если в качестве начальной точки в алгоритме Берлекэмпа – Месси вместо 1 выбрать многочлен Y(х), то модифицированный синдром вычисляется неявно и нет необходимости вводить его в явном виде. Отбросим  теперь  обозначение  L'(х),  заменив  его  на  L (х)  и  назвав многочленом локаторов ошибок и стираний. При начальных условиях, даваемых многочленом Y (х), алгоритм Берлекэмпа — Месси рекуррентно порождает многочлен ло­каторов ошибок и стираний в соответствии с уравнениями

L^(r) (x) = L^{(r -1)} (x) – D_r x B^{(r -1)} (x) ,                          (7.16)

B^(r) (x) = (1 – d_r)x B^{(r -1)} (x) + d_r D_r^-1 L^{(r -1)} (x) ,      (7.17)

 

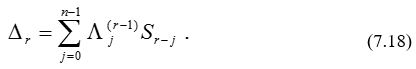
ГЛАВА 8. СТРУКТУРА CRC – КОДА

В дипломной работе используется алгоритм циклических избыточных кодов — Cyclic Redundancy Codes (в дальнейшем СRС). Этот алгоритм  представляет собой  высокоэффективное средство обнаружения ошибок. Благодаря вычислению циклической контрольной суммы мы можем определить искажения данных, так как изменение данных приводит к изменению циклической контрольной суммы. Основным свойством алгоритма является то, что циклическая контрольная сумма изменится как при искажении одного так и более битов информационной последовательности.

При получении циклической контрольной суммы исходные данные, представленные в виде двоичной последовательности : a₀, a₁, a₂,…, a_n-2, a_n-1 , удобно рассматривать, представляя комбинацию двоичного кода в виде характеристического полинома от фиктивной переменной x, а именно :

K(x) = a_n-1x ^n-1 + a_n-2x ^n-2 +…+ a₂x ² + a₁x + a₀ ,

где a_i – цифры двоичного кода исходных данных.

Так например двоичную последовательность 11100110 можно представить в виде полинома :

K(x) = 1x ⁷ + 1x ⁶ +1x ⁵ + 0x ⁴ + 0x ³ + 1x ² + 1x 1 + 0x ⁰ = x ⁷ + x ⁶ +x ⁵ + x ² + x .

Представление двоичной последовательности в виде характеристического полинома позволяет свести действия для получения СRС к операциям над многочленами. При этом сложение двоичных многочленов сводится к сложению по модулю два коэффициентов при одинаковых степенях переменной x ; умножение производится по обычному правилу перемножения степенных функций, однако полученные при этом коэффициенты при одинаковых степенях переменной x складываются по модулю два ; деление осуществляется по правилам деления степенных функций, при этом операции вычитания заменяются операциями суммирования по модулю два. [1]

Процедура получения CRC – кода состоит в следующем :

Исходная последовательность, представленная в виде характеристического многочлена K(x), умножается на одночлен x ⁿ , а затем делится на образующий полином G(x) степени n. В результате умножения K(x) на x ⁿ степень каждого одночлена, входящего в K(x), повысится на n. При делении произведения K(x) · x ⁿ на образующий полином G(x) получится частное — Q(x) такой же степени, как и K(x), и остаток — R(x), степень которого не больше n-1. Результат умножения и деления можно представить в следующем виде:

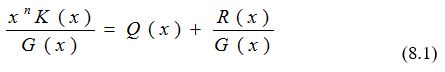
Умножая обе части равенства на  G(x) и проведя некоторые перестановки, получим:

N(x) = xⁿ K(x) + R(x)                                           (8.2)

В правой части формулы знак минус перед R(x) заменен знаком плюс, так как вычитание по модулю два сводится к сложению.

Таким образом, последовательность бит, представляемая собой коэффициенты полинома R(x), добавляемая к информационной последовательности, является циклической контрольной суммой, а итоговой кодовой последовательностью является коэффициенты полинома N(x).

После передачи сообщения по каналу на передаваемую последовательность могут накладываться ошибки, в следствии чего принятая комбинация примет вид :

M(x) = N(x) + E(x),                                          (8.3)

где E(x) – вектор ошибки.

Определить наличие ошибок в принятой последовательности можно с помощью остатка от деления полинома M(x) на образующий полином G(x).  Если E(x) = 0 (ошибок в сообщении нет), остаток от деления равняется нулю, то есть (N(x) + E(x)) mod G(x) = 0 , иначе остаток от деления не равен нулю, что свидетельствует о наличии ошибок в принятой последовательности.

Существует вероятность того что обнаружение ошибок не произойдет при наличии ошибок в принятой последовательности. Это произойдет если вектор ошибок равен порождающему полиному, или является его произведением, то есть E(x) = G(x)A(x).

Так например нужно закодировать двоичную последовательность 11100110 :

K(x) = x ⁷ + x ⁶ +x ⁵ + x ² + x

Порождающий полином выберем G(x) = x ⁴ + x ³ + 1

K(x) · x ⁴ = x ¹¹ + x ¹⁰ +x ⁹ + x ⁶ + x ⁵

R(x) = (K(x) · x ⁴ ) mod G(x) = x ² + x

N(x) = K(x) · x ⁴ + R(x) = x ¹¹ + x ¹⁰ +x ⁹ + x ⁶ + x ⁵ + x ² + x

Теперь допустим произошла ошибка, которой соответствует полином E(x) = x ⁶ + x ⁵ + x ² = G(x) · x ²  в следствии чего

N(x) + E(x) = x ¹¹ + x ¹⁰ +x ⁹ + x   и     (N(x) + E(x)) mod G(x) = 0 .

Остаток от деления равен нулю хотя произошли ошибки. Поэтому для понижения вероятности этого события в качестве порождающего полинома выбирают неприводимый полином, то есть который нельзя разложить на множители. Так же можно понизить вероятность ошибки используя порождающий полином большей степени.

Для решения вышеуказанной задачи применяется множество алгоритмов расчёта CRC. Самыми распространёнными, на данный момент, являются алгоритмы CRC-16, CRC-24, CRC-32. Расчеты показывают, что чем выше степень порождающего полинома, тем меньше вероятность ошибки. Например, используя алгоритм CRC-32, вероятность ошибки составит 1/2³². Для уменьшения вероятности ошибки можно увеличить добавляемый остаток в два раза путем применения CRC – кода последовательно второй раз.

В дипломной работе используется алгоритм CRC-32, что означает применение 32 битного порождающего полинома :

x³² + x²⁶ + x²³ + x²² + x¹⁶ + x¹² + x¹¹ + x¹⁰ + x⁸ + x⁷ + x⁵ + x⁴ + x² + x + 1

Такой полином обеспечивает вероятность ошибки 2^-32 ≈ 2,3 · 10^-10, но в силу того что CRC – код применяется последовательно два раза, остаток становится равным 64 бита, следовательно вероятность ошибки составит           2^-64 ≈ 5,421 · 10^-20.

 

ГЛАВА 9. ПРЕОБРАЗОВАНИЯ СООБЩЕНИЯ

Основной целью данной систем передачи информации является достоверность принятого сообщения, поэтому все действия направлены на то, чтобы принятое сообщение было декодировано точно, то есть совпало с переданным сообщением. В связи с этим передаваемая последовательность кодируется каскадным кодом, внешний код которого является кодом Рида-Соломона с характеристиками (255, K, D), а внутренний – модифицированным кодом Голея с характеристиками (24, 12, 8). Так же к исходному сообщению будет добавляться контрольная сумма CRC, которая будет использована для проверки кодовой последовательности на заключительном этапе, и в случае ее не совпадения будет производиться перебор стертых кодовых слов внутреннего кода до тех пор пока контрольная сумма не совпадет.

В процессе передачи сообщения от источника к потребителю исходное сообщение  трансформируется в различные формы, удобные для той или иной операции. Распишем последовательность преобразований, происходящих с исходным сообщением в процессе операций кодирования и декодирования.

1. Формирование двоичной последовательности исходного сообщения. Оно будет представлено в виде последовательности из N бит :

a₀, a₁, a₂, …, a_N-1 .

2. Вводим первую избыточность данных в виде m бит циклической контрольной суммы CRC, которая используется для проверки кодовой последовательности на заключительном этапе. Таким образом исходное сообщение будет представлено в виде последовательности из N+m бит :

a₀, a₁, a₂, …, a_N-1, a_N, a_N+1, a_N+2, …, a_{N+ m-1} .

3. Поскольку кодирование будет производиться по принципу каскадного кодирования, внешним кодом которого является код Рида–Соломона, определенный над полем GF(2⁸), то необходимо разбить исходную ..последовательность на блоки по 8 бит. .

a₀, a₁,…, a₇,     a₈, a₉,…, a₁₅, …… ,    a_{N+ m-9},a_{N+ m-8},…, a_{N+ m-1}

То есть получается новая последовательность :

a₀, a₁, … , a_{(N+ m) / 8–1} ,

каждый символ которой является элементом поля GF(2⁸). Преобразованная  последовательность будет использоваться как исходная для внешнего кода.

4. Далее данная последовательность кодируется кодом Рида-Соломона с характеристиками (255, K, D) , где

K = (N + m)/8

D = 255 – K + 1

Таким образом вводится избыточность, и последовательность представляется в виде  255 элементов поля GF(2⁸), каждый из которых по 8 бит :

b₀, b₁, … , b₂₅₄ .

5. В качестве внутреннего кода каскадного кода используется код Голея с характеристиками (24, 12, 8). И так как количество информационных символов данного кода равняется 12, то последовательность из 255 элементов по 8 бит нужно разбить на символы над полем GF(2¹²), то есть на 170 элементов по 12 бит.

b₀,    b₁¹ ,      b₁²,   b₂,        b₃,   b₄¹,        b₄²,   b₅,   …

⇓                   ⇓                     ⇓                      ⇓

g₀                 g₁                    g₂                     g₃       … ,

где b_i¹ — первые 4 бита элемента b_i , а b_i² – вторые 4 бита b_i .

Преобразованная  последовательность будет использоваться как исходная для внутреннего кода.

6. Полученная последовательность поэлементно кодируется кодом Голея с характеристиками (24, 12, 8). В итоге последовательность представляется в виде 170 элементов, каждый из которых содержит по 24 бита :

d₀, d₁, … , d₁₆₉ .

7. Перед отправкой преобразованного сообщения на модулятор необходимо произвести еще одно преобразование последовательности, а именно разбиение закодированных блоков на символы алфавита {C_k}, согласованного с модемом :

c₀, c₁, … , c_{170*24 / i -1} ,

где i – количество бит в одном символе алфавита {C_k}, определяется характеристиками модема.

8. Далее закодированная последовательность подается на модем, где преобразуется в последовательность сигналов, которые с передатчика отправляется в эфир.

Процесс восстановления сообщения  на приемной стороне системы передачи информации будет происходить в обратном порядке.

1. Принятый сигнал с помощью модема преобразуется в последовательность кодовых символов :

c₀, c₁, … , c_{170*24 / i -1}

2. Преобразование символов алфавита {C_k}, согласованного с модемом, в последовательность для внутреннего декодера (170´24 бита) :

d₀, d₁, … , d₁₆₉

3. Декодирование кода Голея. Последовательность примет вид 170 блоков по 12 бит :

g₀, g₁ , … , g₁₆₉

4. Преобразование последовательности для внешнего декодера (255´8 бит) :

b₀, b₁, … , b₂₅₄ .

5. Декодирование кода Рида — Соломона. Последовательность примет вид 170 блоков по 8 бит :

a₀, a₁, … , a₁₆₉ .

6. Далее следует вычисление и проверка циклической контрольной суммы CRC. Если проверка дала положительный результат, то полученное сообщение совпадает с переданным и посылается получателю.

 

ГЛАВА 10. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РАЗРАБОТАННОЙ КОДОВОЙ КОНСТРУКЦИИ

Программная реализация разработанной кодовой конструкции осуществлена в среде Microsoft Visual C++ 6.0 . Эта среда разработки программного обеспечения дает такие качества как универсальность применения, логическую стойкость и удобочитаемость исходного кода программы.

Минимальные требования, предъявляемые к компьютеру:

• процессор Pentium II 450 MHz;
• объем оперативной памяти не менее 64Мб (желательно 128 и более)
• монитор SVGA;
• дисковод CD-ROM – для установки приложений Microsoft Visual C++;
• клавиатура;
• мышь;
• объем свободного дискового пространства 10 Мбайт

На компьютере должна быть установлена одна из операционных систем Windows 98, Windows 2000, Windows ME, Windows NT или Windows ХР.

 

ГЛАВА 11. РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ

Разработанная в дипломной работе система передачи информации предназначена для систем передачи информации без обратной связи, где требуется высокая достоверность принятого сообщения. Так как основным критерием является достоверность принятого сообщения, в следствии чего возросла сложность кодовой конструкции и увеличился объем вычислений, то в других системах  данную конструкцию применять не рекомендуется. В системах с обратной связью сложность кодовой конструкции и объем вычислений можно сделать гораздо меньше.

---

Страницы:   1   2   3   4   5

---