СОДЕРЖАНИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПОСТАНОВКА ЗАДАЧИ
- 1.1. Основные задачи дипломной работы
- 1.2. Обоснование возможности восстановления стертых кодовых слов внутреннего кода
- ГЛАВА 2. ПРИНЦИП КАСКАДНОГО ПОСТРОЕНИЯ СХЕМЫ
- 2.1. Обоснование применения каскадного кода
- 2.2. Структура каскадного кода
- ГЛАВА 3. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 3.1. Структура линейных блоковых кодов
- 3.2. Матричное описание линейных блоковых кодов
- 3.3. Совершенные и квазисовершенные коды
- 3.4. Циклические коды
- ГЛАВА 4. СТРУКТУРА КОДА ГОЛЕЯ
- 4.1. Двоичный код Голея
- 4.2. Методы декодирования циклических кодов
- 4.3. Декодер Меггитта для кода Голея
- ГЛАВА 5. КОДЫ БЧХ
- 5.1. Определение кодов БЧХ
- 5.2. Коды Рида – Соломона
- ГЛАВА 6. АЛГОРИТМ БЕРЛЕКЭМПА – МЕССИ
- 6.1. Алгоритм Берлекэмпа – Месси
- 6.2. Ускоренный алгоритм Берлекэмпа – Месси
- ГЛАВА 7. ИСПРАВЛЕНИЕ СТИРАНИЙ И ОШИБОК
- ГЛАВА 8. СТРУКТУРА CRC – КОДА
- ГЛАВА 9. ПРЕОБРАЗОВАНИЯ СООБЩЕНИЯ
- ГЛАВА 10. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РАЗРАБОТАННОЙ КОДОВОЙ КОНСТРУКЦИИ
- ГЛАВА 11. РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- ГЛАВА 12. ОЦЕНКА ЭФФЕКТИВНОСТИ ИНВЕСТИЦИЙ В РАЗРАБОТКУ ПРОГРАММНОГО ПРОДУКТА
- 12.1. Цели, задачи и методы оценки эффективности инвестиций
- 12.2. Выбор и описание разрабатываемого и альтернативного вариантов продукта
- 12.3. Выбор ставки сложных процентов и расчет дисконтного множителя по годам вложения
- 12.4. Расчет вложений на этапе разработки и отладки
- 12.5. Расчет вложений по годам этапа эксплуатации
- 12.6. Расчет показателя современной итоговой величины затрат по сравниваемым вариантам
- ГЛАВА 13. БЕЗОПАСНОСТЬ И САНИТАРНО – ГИГИЕНИЧЕСКИЕ УСЛОВИЯ ТРУДА НА РАБОЧЕМ МЕСТЕ ПОЛЬЗОВАТЕЛЯ ПЭВМ
- 13.1. Микроклимат производственного помещения
- 13.2. Предельно допустимое содержание вредных веществ в воздухе рабочей зоны. Вредные вещества
- 13.3. Защита от производственного шума
- 13.4. Защита от вибрации
- 13.5 Защита от излучений
- 13.6. Электробезопасность
- 13.7. Освещение на рабочем месте
- 13.8. Освещенность рабочего места программиста
- 13.9. Расчет общего искусственного освещения помещения
- 13.10. Общие требования к организации режима труда и отдыха при работе с ВДТ и ПЭВМ
- 13.11. Организация рабочего места
- 13.12. Пожарная безопасность
- ЗАКЛЮЧЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
История кодирования, контролирующего ошибки, началась в 1948 г. публикацией знаменитой статьи Клода Шеннона. Шеннон показал, что с каждым каналом связано измеряемое в битах в секунду и называемое пропускной способностью канала число С, имеющее следующее значение. Если требуемая от системы связи скорость передачи информации R (измеряемая в битах в секунду) меньше С, то, используя коды, контролирующие ошибки, для данного канала можно построить такую систему связи, что вероятность ошибки на выходе будет сколь угодно мала. В самом деле, из шенноновской теории информации следует тот важный вывод, что построение слишком хороших каналов является расточительством; экономически выгоднее использовать кодирование. Шеннон, однако, не указал, как найти подходящие коды, а лишь до¬казал их существование. В пятидесятые годы много усилий было потрачено на попытки построения в явном виде классов кодов, позволяющих получить обещанную сколь угодно малую вероятность ошибки, но результаты были скудными. В следующем десятилетии решению этой увлекательной задачи уделялось меньше внимания; вместо этого исследователи кодов предприняли длительную атаку по двум основным направлениям.
Первое направление носило чисто алгебраический характер и преимущественно рассматривало блоковые коды. Первые блоковые коды были введены в 1950 г., когда Хэмминг описал класс блоковых кодов, исправляющих одиночные ошибки. Коды Хэмминга были разочаровывающе слабы по сравнению с обещанными Шенноном гораздо более сильными кодами. Несмотря на усиленные исследования, до конца пятидесятых годов не было построено лучшего класса кодов. В течение этого периода без какой-либо общей теории были найдены многие коды с малой длиной блока. Основной сдвиг произошел, когда Боуз и Рой-Чоудхури [1960] и Хоквингем [1959] нашли большой класс кодов, исправляющих кратные ошибки (коды БЧХ), а Рид и Соломон [I960] нашли связанный с кодами БЧХ класс кодов для недвоичных каналов. Хотя эти коды остаются среди наиболее важных классов кодов, общая теория блоковых кодов, контролирующих ошибки, с тех пор успешно развивалась, и время от времени удавалось открывать новые коды.
Открытие кодов БЧХ привело к поиску практических методов построения жестких или мягких реализаций кодеров и декодеров. Первый хороший алгоритм был предложен Питерсоном. Впоследствии мощный алгоритм выполнения описанных Питерсоном вычислений был предложен Берлекэмпом и Месси, и их реализация вошла в практику как только стала доступной новая цифровая техника.
Второе направление исследований по кодированию носило скорее вероятностный характер. Ранние исследования были связаны с оценками вероятностей ошибки для лучших семейств блоковых кодов, несмотря на то что эти лучшие коды не были известны. С этими исследованиями были связаны попытки понять кодирование и декодирование с вероятностной точки зрения, и эти попытки привели к появлению последовательного декодирования. В последовательном декодировании вводится класс не блоковых кодов бесконечной длины, которые можно описать деревом и декодировать с помощью алгоритмов поиска по дереву. Наиболее полезными древовидными кодами являются коды с тон¬кой структурой, известные под названием сверточных кодов. Эти коды можно генерировать с помощью цепей линейных регистров сдвига, выполняющих операцию свертки информационной последовательности. В конце 50-х годов для сверточных кодов были успешно разработаны алгоритмы последовательного декодирования. Интересно, что наиболее простой алгоритм декодирования — алгоритм Витерби — не был разработан для этих кодов до 1967 г. Применительно к сверточным кодам умеренной сложности алгоритм Витерби пользуется широкой популярностью, но для более мощных сверточных кодов он не практичен.
В 70-х годах эти два направления исследований опять стали переплетаться. Теорией сверточных кодов занялись алгебраисты, представившие ее в новом свете. В теории блоковых кодов за это время удалось приблизиться к кодам, обещанным Шенноном: были предложены две различные схемы кодирования (одна Юстесеном, а другая Гоппой), позволяющие строить семейства кодов, которые одновременно могут иметь очень большую длину блока и очень хорошие характеристики. Обе схемы, однако, имеют практические ограничения, и надо ждать дальнейших успехов. Между тем к началу 80-х годов кодеры и декодеры начали появляться в новейших конструкциях цифровых систем связи и цифровых систем памяти.
Так как развитие кодов, контролирующих ошибки, первоначально стимулировалось задачами связи, терминология теории кодирования проистекает из теории связи. Построенные коды, однако, имеют много других приложений. Коды используются для защиты данных в памяти вычислительных устройств и на цифровых лентах и дисках, а также для защиты от неправильного функционирования или шумов в цифровых логических цепях. Коды используются также для сжатия данных, и теория кодирования тесно связана с теорией планирования статистических экспериментов. Приложения к задачам связи носят самый различный характер. Двоичные данные обычно передаются между вычислительными терминалами, между летательными аппаратами и между спутниками. Коды могут быть использованы для получения надежной связи даже тогда, когда мощность принимаемого сигнала близка к мощности тепловых шумов. И поскольку электромагнитный спектр все больше и больше заполняется создаваемым человеком сигналами, коды, контролирующие ошибки, становятся еще более важным инструментом, так как позволяют линиям связи надежно работать при наличии интерференции. В военных приложениях такие коды часто используются для защиты против намеренно организованной противником интерференции.
Во многих системах связи имеется ограничение на передаваемую мощность. Например, в системах ретрансляции через спутники увеличение мощности обходится очень дорого. Коды, контролирующие ошибки, являются замечательным средством снижения необходимой мощности, так как с их помощью можно правильно восстановить полученные ослабленные сообщения.
Передача в вычислительных системах обычно чувствительна даже к очень малой доле ошибок, так как одиночная ошибка может нарушить программу вычисления. Кодирование, контролирующее ошибки, становится в этих приложениях весьма важным. Для некоторых носителей вычислительной памяти использование кодов, контролирующих ошибки, позволяет добиться более плотной упаковки битов.
Связь важна также внутри одной системы. В современных сложных цифровых системах могут возникнуть большие потоки данных между подсистемами. Цифровые автопилоты, цифровые системы управления процессами, цифровые переключательные системы и цифровые системы обработки радарных сигналов – все это системы, содержащие большие массивы цифровых данных, которые должны быть распределены между многими взаимно связанными подсистемами. Эти данные должны быть переданы или по специально предназначенным для этого линиям, или посредством более сложных систем с шинами передачи данных и с разделением по времени. В любом случае важную роль играют методы кодирования, контролирующего ошибки, так как они позволяют гарантировать соответствующие характеристики.
Комплексная автоматизация и совершенствование электронных вычислительных машин сопровождаются резким возрастанием объема и скорости передачи и обработки информации. Одновременно повышаются требования к достоверности передачи и обработки информации. Поэтому разработка новых систем передачи информации будет всегда актуальна.
ГЛАВА 1. ПОСТАНОВКА ЗАДАЧИ
1.1. Основные задачи дипломной работы
Задачей дипломной работы является разработка кодовой конструкции, позволяющей исправлять стертые слова внутреннего кода при использовании каскадного кода, внешний код которого является кодом Рида-Соломона, а внутренний – расширенный код Голея (24, 12).
Задачи, которые необходимо решить для выполнения поставленной цели:
1. обоснование использования каскадного кода;
2. выбор внутреннего кода;
3. выбор внешнего кода;
4. разработка способа восстановления стертых кодовых слов внутреннего кода и обоснование его применения;
5. расчет характеристик полученной системы;
6. выработка рекомендаций по использованию кодовой конструкции.
1.2. Обоснование возможности восстановления стертых кодовых слов внутреннего кода
Так как внутренним кодом является код Голея (24, 12, 8), то минимальное кодовое расстояние данного кода равно d = 8, а значит декодер может исправить не более 3 ошибок. Если в кодовом слове Голея было 4 ошибки, то правильное декодирование такого слова будет невозможным, так как на расстоянии Хэмминга равным 4 находятся несколько слов данного кода, а конкретно 6, в следствии чего появятся стертые символы кода Голея, что может привести к неверному декодированию кода Рида – Соломона, в следствии чего контрольная сумма CRC полученной последовательности будет не верна. В такой ситуации становится актуальной проблема восстановления стертых символов.
При восстановлении стертых символов используется обратная связь с перебором символов внутреннего кода, то есть производится перебор кодовых слов этого кода, которые находятся от стертых на расстоянии Хэмминга равным 4, до тех пор пока в результате не выполнится условие совпадения циклической контрольной суммы CRC.
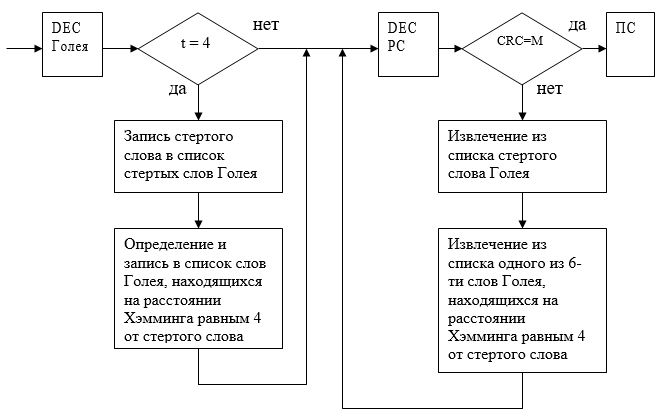
где DEC Голея – декодер Голея (внутренний декодер),
t – число ошибок в кодовом слове Голея,
DEC РС – декодер Рида-Соломона (внешний декодер),
М – циклическая контрольная сумма,
ПС – получатель сообщения
Количество переборов слов внутреннего кода зависит от количества стертых слов nст этого кода, конкретно 6 nст. Среднее число стертых слов во всей последовательности равно :
nст = P{4 ошибки в слове}*170 ,
где P{4 ошибки в слове} = C424 P4ош/бит (1- Pош/бит)20
Pош/бит – вероятность ошибки на бит сообщения для реальных коротковолновых (КВ) каналов, на практике равна 0,04 – 0,07
В реальных условиях при использовании симметричного дискретного канала вероятность ошибки на бит сообщения будем считать равной 0,05 , тогда P{4 ошибки в слове} = 0,0238, а nст » 5. Это означает что производить оптимизацию перебора кодовых слов внутреннего кода не нужно, так как 65 = 7776, что вполне осуществимо на современных вычислительных машинах.
Вычислим вероятности присутствия двух, пяти, восьми стертых слов в последовательности внутреннего кода :
P{n стертых слов} = Cn170 Pn{4 ошибки в слове} (1-P{4 ошибки в слове})170 — n
P{4 ошибки в слове} = 0,0238, следовательно :
P{2 стертых слов} = 0,1423
P{5 стертых слов} = 0,1599
P{8 стертых слов} = 0,0304
Так как для вычисления циклической контрольной суммы CRC используется алгоритм CRC-32, применяемый последовательно два раза, что означает получение 64 – битного остатка, то вероятность ложного набора Pлн =2-64 ≈ 5,421 ·10-20.
Вероятность ложного набора при количестве переборов равном N равна :
Pлн (N) = 1 – (1 – Pлн)N,
где (1 – Pлн)N – вероятность отсутствия ложного набора при N переборах.
В случае если в последовательности внутреннего кода присутствуют 5 стертых слов, то максимальное количество переборов равно 65 = 7776, следовательно вероятность ложного набора Pлн (65) = 4,215 · 10-16 . Если в последовательности внутреннего кода будут присутствуют больше 5 стертых слов, то максимальное количество переборов будет резко возрастать, а с ним и вероятность ложного набора Pлн (N). И если среднее число стертых слов во всей последовательности будет больше 5, то вероятность ложного набора Pлн (N) станет недопустимо большой, в этой ситуации ее можно понизить с помощью увеличения количества разрядов циклической контрольной суммы CRC при применении порождающего полинома большей степени.
Вычислим вероятности ложного набора Pлн (N) при присутствия пяти, шести, семи, восьми стертых слов в последовательности внутреннего кода :
Pлн (65 = 7776) = 4,215 · 10-16
Pлн (66 = 46656) = 2,529 · 10-15
Pлн (67 = 279936) = 1,517 · 10-14
Pлн (68 = 1679616) = 1,091 · 10-13
Вероятность ошибочного декодирования сообщения определяется по следующей формуле :
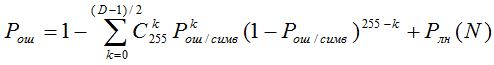
где D – конструктивное расстояние внешнего кода, Pош/симв – вероятность ошибки символа внешнего кода, равная
![]()
Pош/Голея – вероятность ошибки кодового слова Голея, равная :
1) перебор слов внутреннего кода не применяется
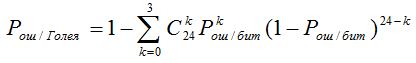
2) перебор слов внутреннего кода применяется
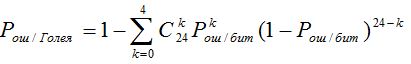
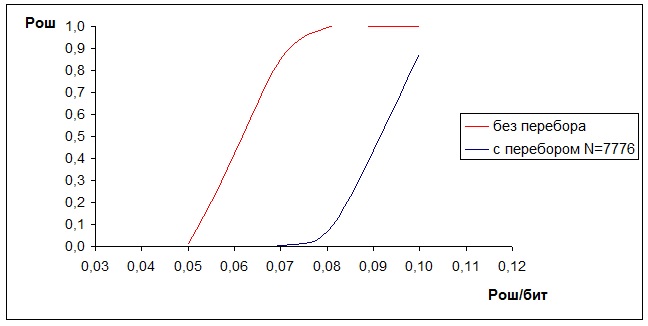
В таблице 1.1. приведены расчеты вероятности ошибочного декодирования сообщения Pош при использовании в качестве внешнего кода –кода Рида-Соломона (255, 235, 21), Pош/бит= 0,05 – 0,1 , количество переборов N равно 65 = 7776, Pлн (65) = 4,215 · 10-16.
Таблица 1.1
| Pош/бит = 0,05 | |||
| N | Pош/Голея | Pош/симв | Pош |
| Без перебора N=0 | 0,0297825 | 0,0199549 | 0,01440870000000000 |
| С перебором N=65 | 0,0059745 | 0,0039870 | 0,00000000991256958 |
| Pош/бит = 0,06 | |||
| Без перебора N=0 | 0,0526036 | 0,0353839 | 0,29460700000000000 |
| С перебором N=65 | 0,0126522 | 0,0084526 | 0,00001427079999958 |
| Pош/бит = 0,07 | |||
| Без перебора N=0 | 0,0830255 | 0,0561459 | 0,85187800000000000 |
| С перебором N=65 | 0,0232641 | 0,0155701 | 0,00245390999999958 |
| Pош/бит = 0,08 | |||
| Без перебора N=0 | 0,1207000 | 0,0821792 | 0,99510000000000000 |
| С перебором N=65 | 0,0385734 | 0,0258838 | 0,06997269999999960 |
| Pош/бит = 0,09 | |||
| Без перебора N=0 | 0,1648210 | 0,1131440 | 0,99997800000000000 |
| С перебором N=65 | 0,0590984 | 0,0397976 | 0,43588100000000000 |
| Pош/бит = 0,1 | |||
| Без перебора N=0 | 0,2142620 | 0,1484990 | 0,99999998580800000 |
| С перебором N=65 | 0,0850749 | 0,0575528 | 0,87232400000000000 |
ГЛАВА 2. ПРИНЦИП КАСКАДНОГО ПОСТРОЕНИЯ СХЕМЫ
2.1. Обоснование применения каскадного кода
При синтезе и анализе информационных систем необходимо оперировать определенными качественными и количественными показателями, позволяющими производить оценку эффективности систем, а также сопоставлять их с другими, подобными им системами.
Под эффективностью системы передачи информации понимается ее способность обеспечить передачу информации с заданной скоростью и достоверностью. Скорость передачи информации определяется количеством информации, передаваемой в единицу времени. Максимально возможную скорость передачи информации принято называть пропускной способностью. Пропускная способность характеризует потенциальные возможности системы, и ее значение определяется теоремой Шеннона.
Наиболее полная количественная оценка эффективности системы передачи информации будет характеризоваться отношением передаваемой информации к затратам, связанным с передачей данного количества информации. Для передачи информации по каналу связи необходимы определенные затраты мощности радиопередающего устройства. Кроме того, для передачи и обработки сигналов необходимо определенное время. Наконец, сигналы, используемые в системе передачи информации занимают определенный диапазон частот. Поэтому эффективность характеризует способность системы обеспечить передачу данного количества информации с наименьшими затратами мощности сигналов, времени и полосы частот.
Для систем передачи информации важной характеристикой является информационная надежность, под которой будем понимать способность системы передавать информацию с заданной достоверностью. Достоверность количественно характеризуется степенью соответствия принятого сообщения переданному.
Снижение достоверности передачи сообщений происходит под воздействием внешних и внутренних (аппаратных) помех. Способность информационной системы противостоять вредному действию помех называют помехоустойчивостью.
Условия, при которых может быть достигнуто повышение помехоустойчивости и скорости передачи информации, являются противоречивыми. Повышение помехоустойчивости практически всегда сопровождается снижением скорости передачи информации и, наоборот, повышение оперативности отрицательно сказывается на помехоустойчивости систем.
Обоснуем целесообразность использования помехоустойчивого кодирования.
В качестве характеристики сигнала часто используют – объем сигнала, который равен : Vс=TcFcHc. Где Tc – длительность сигнала, Fc – ширина спектра сигнала, Hc – динамический диапазон. Объем сигнала Vс дает общее представление о возможностях данного ансамбля сигналов как переносчиков сообщений. Чем больше объем сигнала, тем больше информации можно “вложить” в этот объем и тем труднее передать такой сигнал по каналу связи.
Необходимым условием неискаженной передачи по каналу сигналов с объемом Vс , очевидно, должно быть Vс <= Vк. Преобразование первичного сигнала в высокочастотный сигнал и преследует цель согласования сигнала с каналом. В простейшем случае сигнал согласуют с каналом по всем трем параметрам, т.е. Tс <= Tк ; Fс <= Fк ; Hс <= Hк . При этих условиях объем сигнала полностью “вписывается” в объем канала. Однако это условие может выполняться и тогда, когда одно или два из неравенств не выполняется. Это означает, что можно производить “обмен” длительности на ширину спектра или ширину спектра на динамический диапазон и т.д.
Следовательно, если мы увеличим длительность сигнала, то уменьшится ширина спектра сигнала и его динамический диапазон, что важно при использовании широкополосных помехоустойчивых видов модуляции. По этому во избежании всех выше перечисленных проблем будет выгоднее использовать помехоустойчивое кодирование.
Далее обоснуем применение именно каскадного кода с внешним кодом Рида – Соломона.
Из теории информации известно, что дискретный канал без памяти обладает некоторой пропускной способностью С, такой что для любых скоростей передачи R, меньших С, существуют коды, которые при декодировании по критерию максимума правдоподобия обеспечивают сколь угодно малую вероятность ошибки. Согласно этой теореме может быть найден (методом проб и ошибок) соответствующий код. Для его технической реализации кодер должен хранить некий словарь из кодовых слов, а декодер должен быть способен вычислять переходную вероятность передаваемого кодового слова в принятый для каждого кодового слова. Однако в этом случае размеры кодера и число вычислений, которые придется выполнять декодеру, увеличиваются по экспоненциальному закону с ростом длины блока N, и если с ростом длины блока вероятность ошибки уменьшается по экспоненциальному закону, то с ростом сложности системы она уменьшается лишь по степенному закону.
В связи с этим возникает проблема нахождения такого кода и соответствующего метода декодирования, чтобы сложность кодера и декодера, реализующих этот метод, возрастала с увеличением длины кода N гораздо медленнее, чем по экспоненте. Использование линейных кодов в значительной мере решает проблему кодирования блочных кодов, так как для класса линейных кодов зависимость сложности кодера от N имеет линейный характер. Такими же свойствами обладают сверточные или рекуррентные коды.
Существуют два подхода к решению проблемы уменьшения сложности декодера. Один из них, иногда называемый вероятностным, состоит в поисках более эффективных, чем простое сравнение, способов реализации декодирования, подобно декодированию по критерию максимума правдоподобия. Важным результатом, полученном на этом пути, является последовательное декодирование, которое может быть использовано для сверточных кодов. Однако при всей своей привлекательности последовательное декодирование обладает тем недостатком, что количество вычислений в этом способе декодирования является переменной величиной и требует применения буферного накопителя, вероятность переполнения которого снижается лишь по степенному закону с увеличением его размеров. Кроме того, при последовательном декодировании скорость не может превышать некоторый предел R¢, значение которого меньше пропускной способности. Второй подход, иногда называют алгебраическим, заключается в том, что для облегчения поиска эффективного алгоритма декодирования при выборе кода используются структуры, изучаемые в современной алгебре. Выдающимся результатом, полученном на этом пути, являются коды Боуза-Чоудхури-Хоквингема (коды БЧХ). Коды БЧХ небольшой длины весьма эффективны, однако при больших длинах их эффективность падает, так как при больших длинах кодового слова n либо d/n ®0 либо r® n ( где d это минимальное расстояние кода, а r число проверочных символов ).
В дипломной работе использован подход к построению системы связи, основанный на кодировании и декодировании по каскадному принципу. Он объединяет алгебраический и вероятностный подходы, позволяя получить достаточно длинные коды, для которых при возрастании длины блока вероятность ошибки в каналах без памяти уменьшается по экспоненте, а сложность декодера возрастает лишь как небольшая степень длины блока. Это свойство сохраняется для всех скоростей передачи, меньших пропускной способности. В этом смысле оно позволяет нам в значительной степени приблизиться к осуществлению тех возможностей, которые излагаются в теореме Шеннона.
2.2. Структура каскадного кода
Одним из путей построения блоковых кодов с большими длинами является каскадирование кодов. Этот прием состоит в сочетании кода с символами из малого алфавита с кодом с символами из алфавита с большим объемом. Представим себе последовательность q-ичных символов длины kK. Эту последовательность можно разбить на K блоков по k символов и рассматривать каждый такой блок как элемент qk-ичного алфавита. Последовательность из K таких элементов кодируется ( N, K ) – кодом, заданным над полем GF(qk). Затем каждый из N получившихся qk-ичных символов представляется в виде последовательности из k q-ичных символов и кодируется q-ичным (n, k) – кодом. Таким образом, каскадный код имеет два различных уровня кодирования.
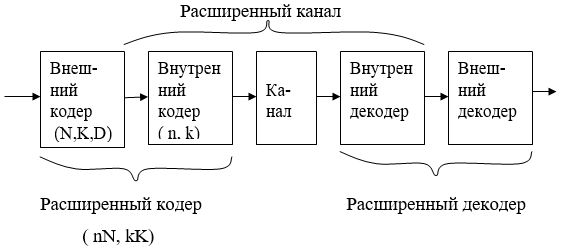
Легко видеть, что для такого расширенного канала можно создать код с длиной n и кодовой скоростью r = k/n. Применительно к исходному каналу этот блочный код имеет полную длину N0=nN, а его результирующая скорость передачи равна R0=rR, где R = K/N. Кодер этого длинного блочного кода может состоять из двух последовательно соединенных кодеров, а декодер – из двух декодеров, рассчитанных на более короткие коды.
В качестве внешнего кода целесообразно применять код Рида-Соломона. Этот выбор обусловлен ниже сказанным.
Из теоремы кодирования следует, что при любой скорости передачи, меньшей пропускной способности канала, убывание вероятности ошибки с увеличением общей длины кодовой комбинации происходит по экспоненте, показатель которой несколько меньше максимально возможной величины, причем такое убывание обеспечивается двухступенным каскадным кодом, второй ступенью которого является код Рида-Соломона. Сложность декодирования такого каскадного кода определяется в основном сложностью декодирования кода Рида-Соломона, которое осуществляется применением эффективных алгоритмов декодирования, основанных на использовании их алгебраической структуры, позволяющей использовать алгоритмы быстрых вычислений, в частности быстрое преобразование Фурье.
Из выше сказанного видно, что наиболее выгодным сочетанием скорости декодирования и помехоустойчивости является использование двухступенного каскадного кода, второй ступенью которого является код Рида-Соломона. Именно этот принцип и будет использоваться в дипломной работе.
ГЛАВА 3. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
3.1. Структура линейных блоковых кодов
Большинство известных хороших кодов принадлежит классу линейных кодов. Этот класс кодов определяется специально выбираемой структурой кода. Рассмотрим структуру линейных блоковых кодов.
Векторное пространство GF n (q) представляет собой множество n – последовательностей элементов из GF(q) с покомпонентным сложением и умножением на скаляр. Наиболее важным частным случаем является GF n (2) – векторное пространство двоичных слов длины n, в котором при сложении двух векторов в каждой компоненте происходит сложение по модулю 2.
Линейный код есть подпространство в GF n (q). Таким образом, линейный код есть непустое множество n – последовательностей над GF(q), называемых кодовыми словами, такое, что сумма двух кодовых слов является кодовым словом, и произведение любого кодового слова на элемент поля также является кодовым словом.
Каждое слово в линейном коде связано с остальными словами кода так же, как любое другое кодовое слово. Расположение соседних кодовых слов вокруг нулевого слова есть типичное расположение слов вокруг любого другого кодового слова. Например, предположим, что с – некоторое кодовое слово и с1, …., сr – кодовые слова, находящиеся на некотором расстоянии d от с ; тогда с – с – нулевое слово и с1 – с, с2 – с, …., сr – с – кодовые слова, находящиеся на расстоянии d от нулевого слова. Таким образом, для определения минимального расстояния линейного кода достаточно определить расстояние между нулевым словом и ближайшим к нему другим кодовым словом.
Вес Хемминга w(c) кодового слова с равен числу его ненулевых компонент. Минимальный вес кода w* есть минимальный вес ненулевого кодового слова. Для линейного кода минимальное расстояние d* находится из равенства :
d* = min w(c) = w*(c), (3.1)
где минимум берется по всем кодовым словам, кроме нулевого.
Следовательно, для нахождения линейного кода, исправляющего t ошибок, необходимо найти линейный код с минимальным весом, удовлетворяющем неравенству w* >= 2t + 1 .
