Реферат на тему «Применение математической модели в лесотехнической промышленности»

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

1. Понятие математического моделирования

2. Применение математической модели в лесотехнической промышленности

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

Сложная социально-экономическая ситуация в России, обострение конкуренции среди промышленных предприятий и необходимость снижения себестоимости производимой продукции все настоятельнее требуют повышения эффективности производства, более рационального расходования имеющихся в его распоряжении финансовых и материальных средств и ресурсов, повышения производительности труда. Сложное финансовое, положение многих предприятий и проблемы поиска инвестиций, часто не удается добиться повышения эффективности производства за счет экстенсивных факторов или расширения производства, его существенной реструктуризации и модернизации, освоения новой, более совершенной и конкурентоспособной продукции. Учитывая эти факторы, промышленный сектор страны стал применять моделирование для прогнозирования, учета, с целью обезопасить свои предприятия. Именно поэтому можно считать данная тема в современном мире актуальна.

Идея моделирования состоит в замене реальной системы, машины или механизма моделью, которая находится с ними в соответствии и способна максимально точно воспроизводить свойства или характеристики реальной системы, то есть эффективно решать все задачи экспериментального исследования. Под моделированием предполагается описание посредством математических уравнений и неравенств реальных процессов. Моделирование позволяет значительно сократить объём экспериментальных исследований и сроки проектирования объектов. Если результаты моделирования подтверждаются, то они могут служить базисом для дальнейшего прогнозирования процессов, протекающих в исследуемых объектах. При этом адекватность модели зависит от цели моделирования и принятых критериев.

Целью данной работы можно считать рассмотрение понятия математическое моделирование и его применяемость в лесотехнической промышленности.

1. Понятие математического моделирования

Первоначально определение «моделирование» использовалось для изучения проблем и вопросов, которые не получалось решить с помощью теории и эксперимента.

Моделирование — процесс рассмотрения и изучения различных явлений на физических моделях. С помощью моделей можно воспроизводить изучаемые явления, которые являются оригиналами, при этом сохранять природу возникновения и внешний вид оригинала, при этом отличительной особенностью могут быть размеры, скорость протекания процесса и материал, и другие факторы, и это именно приводит к изменению параметров.

Чаще всего используют два основных метода моделирования, такие как физический и математический. Физический метод основан на изучении модели, которая имеет одинаковую природу с оригинальным образцом. Этот метод может заменить эксперимент, а это очень ценно для изучения сложных машин и систем. Также, стоит учесть, что с помощью данного метода можно изучать явления, происходящие в системе оригинала, при этом сохраняя его природу.

Совокупность математических объектов и зависимость между ними, описывающая свойства технического объекта формирует математическую модель системы или механизма в целом. Математическая модель позволяет рассматривать различные характеристики, а также помогает оценить возможность использования определенной системы или механизма.

Математическое моделирование, может быть использовано в двух направлениях, таких как:

—      построение моделей на основе прямой аналогии.

—      построение моделей на основе компьютерного моделирования.

К первому направлению можно отнести сеточные электрические модели для решения дифференциальных уравнений в частных производных.

Математическое моделирование предполагает определение процесса на основе анализа его математического описания с помощью ПК и соответствующего программного обеспечения. При этом под моделью понимают математическую модель, преобразованную к виду (языку программирования и интерфейсу), удобному и понятному для применения ЭВМ.

При решении практических задач нужно пользоваться схемой действий, представленной на рисунке 1.

Рисунок 1 – Схема действий при решении задач

Математическое формулирование задачи можно представить в форме геометрических фигур, различных функции, неравенств, систем уравнений и т.п. Описание объекта либо явления можно представить в виде: непрерывной формой либо дискретной, детерминированной или стохастической, либо другими.

Первоначальная теория о математическом моделировании гласила о получении закономерностей протекания различных явлений либо работы механизмов. А в нынешнее время теория математического моделирования обеспечивает выявление закономерностей протекания различных явлений окружающего мира или работы систем и устройств путем их математического описания и моделирования без проведения натурных испытаний. При этом используются положения и законы математики, описывающие моделируемые явления, системы или устройства на некотором уровне их идеализации.

Математическая модель – система, составленная на некотором абстрактном языке, в виде формул, выражений, неравенств и др. Функцию имитации деятельности явления — оригинала должна выполнять именно модель.

Математическая модель всегда описывает только существующий объект либо явление, насколько возможно приближенностью к реальности. Ее вид напрямую зависит от природы реального объекта, так и от задач исследования.

Общественная деятельность, поведение экономики в определенный процесс времени, и многое другое можно смоделировать математически. Это осуществляется сложное работой, требует сверхмощного оборудования, а также крупного квалифицированного персонала. Но несмотря на это, математическое моделирование сложных процессов и явлений экономит финансовые ресурсы, так как, например, на проведение эксперимента требуется гораздо дороже. Умелое использование математического моделирования позволяет избежать многих экологических катастроф, например, позволяет отказаться от испытаний ядерного и термоядерного оружия.

На уровне решений несложных задач и заданий, сейчас можно на любом ПК создать математическую модель. Примером может служить разбор механики либо изучение электронных микросхем электроники в программах Mathcad и MatLab. Для инженеров, созданные программные продукты для создания 3D-моделей деталей, конструкций, улучшают процесс проектирования и конструирования. Создаются комплектные довольно сложные математические модели, которые вводятся в повседневную жизнь, например, телекоммуникационные системы, online – кинотеатры и др.

Цель любого моделирования – анализ реальных данных как в природе, так и в технике. Для выполнения цели необходима формализация математического моделирования, как процесса исследования. Любую модель представляют в виде математического выражения, состоящее из переменных,

поведение которых аналогично поведению реальной системы. Модель может включать элементы случайности, которые учитывают вероятности возможных действий двух или большего числа «игроков», как, например, в теории игр; либо она может представлять реальные переменные параметры взаимосвязанных частей действующей системы.

Для изучения характеристик объектов, систем математическое моделирование делят на аналитическое, имитационное и комбинированное. А вот, математическую модель условно можно разделить на имитационную и аналитическую.

В работе с любым моделированием возникает множество проблем, рассмотрим основные сложности, связанные с математическим моделированием:

—      Модели образуются на определенных допущениях, и соответственно, это приводит к тому, что результаты не могут превышать заложенных в начале допусков.

—      Часто приходиться упрощать начальные допущения, но это не означает, что результаты будут неточными. Желательно избегать лишних допущений. Также существует мнение, что модели лучше создавать как можно простым языком и простой структурой. Но это имеет место быть лишь до того предела, когда модель продолжает отражать реальные процессы, протекающие в системе или объекте.

2. Применение математической модели в лесотехнической промышленности

При рассмотрении данного вопроса, стало ясно, что математическое моделирование применяется во всех сферах жизнедеятельности человека. Рассмотрим подробно применение математического моделирования в лесотехнической промышленности.

При моделировании техпроцессов основой является формирование задачи, которая должна быть экономически выгодной для процесса производства. После простановки поставленных целей и задач необходимо выбрать конкретные выражения показателей в виде конкретных математических зависимостей и отношений. Создание экономико-математических моделей очень трудоемкий процесс.

Математическая модель экономической эффективности технологического процесса функционирования лесотехнического предприятия выстраивается комплексно. Одна из частей показателей модель находится аналитическим методом, а другая – статистическим методом. Данный способ позволяет получить наилучшие результаты.

Любая производственно-экономическая система (ПЭС) имеет главную цель – получение требуемой прибыли производства. Экономическую эффективность ПЭС, в лице лесотехнического предприятия, в условиях рыночной экономики определяет прибыльность функционирования технологической системы в виде различных типов техпроцессов, систем машин и оборудования для их реализации. Какой не была б стабильная ситуация на рынке, все может поменяться в любое время, спрос на продукцию может как увеличиваться, так и уменьшаться. Исходя из этого, любая производственно-экономическая система должна быть устойчивой на рынке и стараться обезопасить свое производство.

Для реализации такой политики деятельности ПЭС предприятие должно обладать определенной производственной мощью, обеспечивающей формирование надежного бизнеса. Также стоит учитывать, что работа предприятий направлена на выпуск определенного объема и качества товара, которые обеспечивали бы получение максимума прибыли ПЭС.

Для лесотехнической промышленности Дальневосточного региона РФ возможны различные варианты техпроцессов продукции:

—        производство лесоматериалов;

—        производство пиломатериалов;

—        производство топливной щепы из низкотоварной древесины и древесных остатков, и отходов лесопиления и др.

Для рассмотрения применения математического моделирования взята проблема места переработки древесного сырья. Анализ мест переработки древесного сырья по социальным, экономическим, экологическим и техническим факторам реализации показал, что задачу выбора приоритетных технологий можно разбить на два этапа. Первый этап связан с проблемой определения структуры и метода организации модельных лесопромышленных участков с целью реализации комплексной переработки древесины на верхних лесопромышленных складах. Это позволит уменьшить издержки на транспортировку древесного сырья. Таким образом, обосновывается эффективная промышленная структура переработки низкотоварной древесины в условиях лесосеки с решением вопросов специализации и концентрации производства продукции на базе новых технологий и оборудования.

Оставшаяся после первого этапа часть объема древесных отходов сырьевой базы по ЛПП на втором этапе привязывается к пунктам переработки древесины для производства продукции специализированного характера.

Полная схема глубокой переработки древесного сырья лесопромышленным предприятием представлена на рисунке 1.

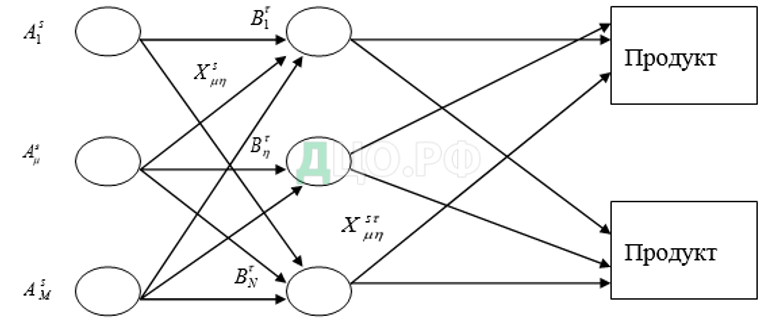
Рисунок 1 — Полная схема глубокой переработки

Возникновение сложной задачи размещения производства с концентрацией различных видов низкотоварной древесины и древесных остатков в местах их возможной переработки с расчетом следующих параметров:

объемы отходов s вида в µ-м пункте (м³);

объемы поставки сырья s из пункта µ в пункт переработки η (м³);

расчетная мощность переработки продукта технологией в η-м пункте переработки (м³);

объемы поставок продукции, изготовленной по технологии в η-м пункте (м³).

Так как существует большое количество различий в деятельности лесозаготовительных предприятий, к ним можно отнести различная удаленность от электросетей, различные природно-производственные факторы и др., задачу выбора главных технологий можно разделить на две составляющие:

• получение готовой продукции и переработка низкотоварной древесины и древесных остатков силами лесопромышленных предприятий в условиях лесосеки (верхнего лесопромышленного склада);
• получение готовой продукции и переработка низкотоварной древесины и древесных остатков силами лесопромышленных предприятий в условиях нижнего лесопромышленного склада.

Показателем экономической эффективности является значение прибыли предприятия от реализации продукции, полученной из всего объема древесины, отпущенной в рубку. Этот показатель учитывает экономическую эффективность техпроцесса, также и уровень использования древесного сырья, а вот из этого можно выразить и степень занятости населения. Таким образом, комплексно отражаются основные критерии устойчивого лесопользования – экономический, экологический, социальный. С учетом этих особенностей, объективная и достаточно комплексная оценка при выборе рационального технологического процесса предприятия должна осуществляться по показателю прибыли F от реализации товарной продукции, получаемой предприятием со всего осваиваемого лесного массива за расчетный период.

Математическая модель экономической эффективности технологического процесса для любой лесосеки арендуемого лесного массива предприятия может быть представлена в общем виде:

общий объем сырья s, полученный с µ лесосеки и доставленный в η пункт переработки за четный период;

средневзвешенная стоимость единицы готового изделия полученной на η пункте переработки за расчетный период;

коэффициент переработки древесного сырья s в η-м пункте переработки по τ-й технологии;

ожидаемые суммарные удельные приведенные затраты на весь расчетный период.

Удельные приведенные затраты – это затраты на единицу продукции, приведенные к одному (чаще всего отчетному) периоду времени. Определение приведенных затрат должно базироваться на учете всех основных факторов, действующих дифференцированно при различных видах рубок и влияющих на воспроизводство леса, а также на учете динамики показателей древостоя. Динамика запаса отдельных секций лесосек лесного массива будет определять также схему транспортного освоения лесного массива. Здесь может быть несколько характерных случаев:

1. Имеется уже сложившийся основной транспортно-технологический процесс, при этом требуется принять такую систему лесозаготовительных машин перерабатывающего оборудования, которая бы имела минимальные приведенные затраты. Ограничением вариантов здесь может быть существующий тип техпроцесса предприятия, который определяется видом вывозимого из лесосек товара (деревья, хлысты, сортименты или готовой продукцией в виде пиломатериалов или технологической щепы).
2. Нет сложившегося транспортно-технологического процесса. В этом случае встает вопрос о целесообразности того или иного варианта технологического процесса, включая и транспортное освоение всего лесосечного фонда или его части.

С учетом изложенного, общая для обоих случаев функция для нахождения рационального техпроцесса для µ лесосеки будет иметь вид

где показатели С отвечают за себестоимость устройств, техники; показатели П – отвечают за производительность машин и техники, К – показатель капиталовложений в технику, Т – срок окупаемости затрат на технологию.

В рассматриваемой математической модели предположено, что суммарные запасы ( ) меньше суммарных потребностей ( ), и это может быть выражено неравенством:

При этом функция принимает вид открытой модели в том случае, если суммарные потребности превышают суммарные запасы. В этом случае вводится фиктивный поставщик A_m+1, запасы которого определяются по формуле:

Стоимость перевозки единицы груза от фиктивного поставщика полагают равным нулю, так как груз в обоих случаях не перевозится. После преобразований задача принимает вид закрытой модели и решается обычным способом.

Сравнение общей стоимости реализованной продукции, которую можно получить при проведении на µ лесосеке различных рубок, характеризует не только тот или иной вид рубки, но и экологический ущерб от них и производится в виде зависимости

ЗАКЛЮЧЕНИЕ

Целью любого моделирования является в получении рабочей системы, которая помогает обеспечивать деятельность человека. Важной процедурной концепцией анализа эффективности является определение периода неустойчивой работы и устранение искажения, вносимого статистическими данными, собранными за такой период.

Полученное с помощью математической модели конкретное оптимальное решение является наилучшим только в рамках использования именно этой модели. Другими словами, оно является наилучшим из всех возможных только тогда, когда выбранный критерий оптимизации можно считать полностью адекватным целям организации, в которой возникла исследуемая проблемная ситуация.

Подводя итог работы, необходимо сказать, что при создании модели желательно применять одновременно все оптимизации. Созданная математическая модель для анализа мест переработки древесного сырья помогает улучшать эффективность деятельности предприятия как в целом, так и в частном. Такие образом, можно считать, что цель работы выполненной.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Информационные технологии и вычислительные системы: Обработка информации и анализ данных. Программная инженерия. Математическое моделирование. Прикладные аспекты информатики / Под ред. С.В. Емельянова. — М.: Ленанд, 2015. — 104 c.
2. Александров, А.Ю. Математическое моделирование и исследование устойчивости: Учебное пособие / А.Ю. Александров, А.В. Платонов и др. — СПб.: Лань, 2017. — 320 c.
3. Алпатов, Ю.Н. Математическое моделирование производственных процессов: Учебное пособие / Ю.Н. Алпатов. — СПб.: Лань, 2018. — 136 c.
4. Горбунов, В.К. Математическое моделирование рыночного спроса: Учебное пособие / В.К. Горбунов. — СПб.: Лань, 2018. — 212 c.
5. Миненко, С.Н. Экономико-математическое моделирование производственных систем / С.Н. Миненко. — М.: МГИУ, 2008. — 140 c.
6. Федоткин, И.М. Математическое моделирование технологических процессов промышленности / И.М. Федоткин. — М.: КД Либроком, 2018. — 416 c.
7. Яглом, И.М. Математические структуры и математическое моделирование / И.М. Яглом. — М.: Ленанд, 2018. — 144 c.