Теория механизмов и машин

Вид работы: Задание

Тема: Теория механизмов и машин

Методические рекомендации по выполнению задания.

Тема «Зубчатые передачи»

1. Произвести геометрический расчет зубчатой передачи при заданных смещениях х₁ и х₂.
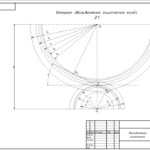
2. Построить картину зубчатого зацепления.

При выполнении задания студент должен:

1. Произвести геометрический расчет зубчатой передачи при заданных смещениях х₁ и х₂.
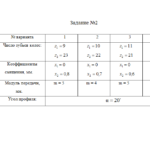
2. Результаты расчетов занести в таблицу 2.1.
3. После выполнения расчетов необходимо вычертить зубчатую передачу (Рис.2.1) в масштабе на бумажном листе формата А3, проставив все размеры. Чертежи также можно выполнить в графической программе Компас-3D (Версии 12–15) или в любой другой графической программе, но переслать по электронной почте в формате «Картинка», сохранив в JPEG или PDF. Можно выполнить чертеж на листе ватмана, затем также переслать в формате «Картинка».
   Варианты заданий распределяются согласно алфавиту.

Пример: Допустим, задан зубчатый механизм, показанный на рисунке 3.1.

Число зубьев колес равняется:

Z₁ = 16,  Z₂ = 60,  Z₂΄ = 18,  Z₃ = 30,  Z₄ = 28,  Z₅ = 26,  Z₆ = 24.

Угловая скорость звена 1: ω₁ = 250 рад/с.

Модуль зубчатых колес: m = 2,5 мм.

Требуется найти число зубьев колеса 3′ (Z₃΄= ?), и определить степень подвижности механизма W.

Решение. Степень подвижности данного механизма определяется по формуле Чебышева:

где

• n = 5 – число подвижных звеньев механизма (1, 2-2′, 3-3′, Н-5, 6);
• p₅ = 5 – количество одноподвижных кинематических пар 5 класса (0-1, 2-0, 3-Н, Н-0, 6-0);
• p₄ = 4 – количество двухподвижных кинематических пар 4 класса (1-2, 2′-3, 3′-4, 5-6).

Стойка – неподвижное звено, всегда имеет обозначение 0.

Рассчитаем, исходя из условия соосности, недостающее количество зубьев у колеса 3′. Условие соосности заключается в том, чтобы геометрические оси ведущего и ведомого валов совпадали. Составим условия соосности.

Следует отметить, что для каждого типа планетарного механизма оно индивидуальное:

• механизм а;
• механизм б;
• механизм в;
• механизм г.

Так как r – радиус делительной окружности равен , а модуль колес m = const, то есть одинаковый для всех звеньев механизма, то можно утверждать, что радиус колеса равен числу зубьев Z этого же колеса и можно записать условие соосности через числа зубьев колес:

• механизм а;
• механизм б;
• механизм в;
• механизм г.

В заданном многоступенчатом редукторе можно выделить три ступени (Рис. 3.3): А и С – простые ступени, Б  – планетарная ступе­нь.

Определим недостающее количество зубьев у колеса 3′, воспользовавшись условием соосности для планетарного механизма типа а.

 

Полное передаточное отноше­ние редуктора будет равно произведению передаточных отношений ступеней, входящих в редуктор. Для схемы редуктора на рис. 3.3 полное передаточное отношение определяется по формуле:

Передаточное отношение ступени А, состоящей из зубчатых колес 1 и 2, определяется по формуле:

 

Аналогично определяем передаточное отношение ступени С, состоящей из зубчатых колес 5 и 6.

Знак плюс относится к внутреннему зацеплению, а знак минус – к внешнему.

Передаточное отношение заданного механизма (ступень Б) получаем из формулы Виллиса для планетарного механизма:

где m – количество внешних зацеплений.

Передаточное отношение всего механизма:

Прикрепленные файлы:

Бланк выполнения задания

Варианты задания (1)

Варианты задания

Документ Microsoft Office Word

задача 2 — чертёж

Приложение 2

Пример выполнения задания