Задача 1
В урне 9 белых и 6 черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми?
Решение:
Вероятность события равна отношению числа исходов, благоприятствующих наступлению события, к общему числу исходов:
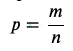
Общее число исходов равно числу способов, которыми можно вынуть 2 шара из 15 имеющихся:
![]()
Событие A состоит в том, что два случайно взятых шара окажутся белыми. Число благоприятствующих этому исходов равно числу способов вынуть 2 шара из 9 имеющихся:
![]()
Тогда, вероятность события А равна:

Ответ: вероятность того, что оба шара окажутся белыми, равна 0,343.
Задача 2
В студенческой группе организована лотерея. Разыгрываются две вещи стоимостью по 1000 руб. и одна стоимостью 3000 руб. Составить закон распределения суммы чистого выигрыша для студента, который приобрел один билет за 100 руб.; всего продано 50 билетов.
Решение:
Испытание состоит в том, что студент играет в лотерею.
Исход испытания может быть следующий: не выиграет в лотерее, выиграет 1000 руб., выиграет 3000 руб. Величина чистого выигрыша при этом соответственно составит: -100; 900 или 2900 руб.
Определим вероятности возможных выигрышей.
Выигрыша нет (всего 3 выигрышных билета, 47-без выигрыша):
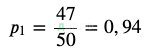
Выигрыш составит 1000 рублей (таких 2 выигрышных билета):
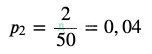
Выигрыш составит 3000 рублей (таких 1 выигрышный билет):
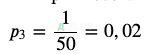
Составим закон распределения для чистого выигрыша:
|
| -100 | 900 | 2900 |
|
| 0,94 | 0,04 | 0,02 |
Проверим выполнение нормировки:
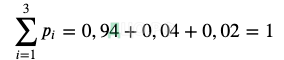
Прикрепленные файлы: |
|
|---|---|

|
Администрация сайта не рекомендует использовать бесплатные работы для сдачи преподавателю. Эти работы могут не пройти проверку на уникальность. Узнайте стоимость уникальной работы, заполните форму ниже: Узнать стоимость |

|
Скачать файлы: |
|
|
|
