Модернизация мостового крана с целью увеличения его грузоподъемности с 8 до 12,5 тонн. Часть 2

1  2  3

---

1.2.6 Выбор тормоза

 

Согласно правилам РОСТЕХНАДЗОРА РФ в данном механизме передвижения должен быть установлен тормоз, т.к. тележка, предназначенная для работы в помещении на надземном рельсовом пути, перемещается со скоростью больше 0,53 м/с.

Расчетный тормозной момент механизма при работе крана в закрытом помещении определяется для движения тележки без груза, под уклон. в предположении, что реборды колес не задевают головки рельсов:

M=M_У+M_ИН-M_ТР , (25)

где M_У — момент, создаваемый уклоном пути.

Рассчитывается по формуле:

M_У= , (26)

где W_У — сопротивление передвижению тележки, создаваемое уклоном (a — уклон рельсового пути): W_У=a×G_T , W_У =0,002×29430=59 Н.

M_У= 0,5 Н×м,

где M_ИН — момент, создаваемый инерцией. Рассчитывается по формуле:

M_ИН= , (27)

где W_ИН — сопротивление передвижению тележки, создаваемое инерцией (d — коэффициент, учитывающий инерцию вращающихся масс механизма; при скорости менее 1 м/с d=1,25): W_ИН=d×m_T×а, W_ИН =1,25×3000×0,07=263 Н.

M_ИН= 5 Н×м.

где M_ТР — момент, создаваемый трением. Рассчитывается по формуле:

M_ТР= , (28)

где W_ТР — сопротивление передвижению тележки, создаваемое трением ( =1,25 – коэффициент, учитывающий сопротивление движению тележки от троллейного токопровода):

W_ТР= , (29)

W_ТР= =338 Н.

M_ТР= 5 Н×м.

M=0,5+5-5= 1 Н×м

По рассчитанным параметрам установленный колодочный тормоз с электромагнитным приводом переменного тока ТКГ-200 со следующими характеристиками: Т_ном=250Н×м, m=38кг удовлетворяет условиям расчёта.

 

1.2.7 Выбор соединительных муфт

 

Муфты выбираем в зависимости от передаваемого вращающего момента и условий работы по формуле:

М_Р=К×М_КР£[М_КР], (30)

где М_Р — расчетный вращающий момент;

К — коэффициент запаса прочности;

М_КР — действующий вращающий момент;

[М_КР] — допускаемый вращающий момент для муфты.

Коэффициент запаса прочности: К=К₁×К₂×К₃ (В этой формуле:

К₁ — коэффициент, учитывающий степень ответственности соединения,

К₂ — коэффициент режима работы, К₃ — коэффициент углового смещения).

Подбираем муфты:

для тихоходного вала редуктора: K=1,8×1×1,25=2,25.

М_КР=353 Н×м, тогда М_Р=2,25×353=794 Н×м.

Выбираем зубчатую муфту с М_К=1000 Н×м.

для быстроходного вала редуктора: K=1,8×1×1=1,8.

М_Р=1,8×5,7=10 Н×м.

Выбираем втулочно-пальцевую муфту с тормозным шкивом, с номинальным вращающим моментом, М_К=250 Н×м

 

2 РАСЧЕТ ДОЛГОВЕЧНОСТИ ПОДШИПНИКА ОПОРЫ БАРАБАНА

 

С=86 кН – динамическая грузоподъемность, [4];

p=10/3 – показатель степень для шарикоподшипников, [4];

L – долговечность подшипника, ч.;

F – эквивалентная нагрузка;

n=16 об/мин – частота вращения внутреннего кольца подшипника.

где Р – нагрузка на барабан, Р=21491 Н.

Н <86000 H.ч.

11230>10000 ч, что удовлетворяет условию.

 

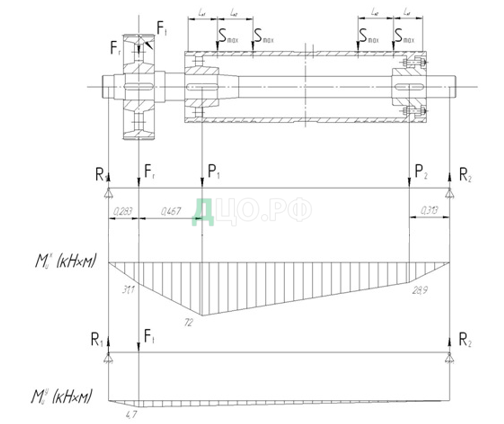
3 ПРОВЕРКА БАРАБАНА НА ИЗГИБ И КРУЧЕНИЕ

 

Нагрузки на ступицы барабана (при пренебрежении его весом) рис. 8:

где l_н – длина нарезанной части;

l_гл – длина гладкой части барабана;

l₁ – расстояние от ступицы барабана до опор вала.

Определяем коэффициент запаса прочности s в опасном сечении (под левой ступицей барабана):

где s_σ – коэффициент запаса прочности по нормальным напряжениям;

s_τ – коэффициент запаса прочности по касательным напряжениям.

где σ_-1 = 379 МПа – предел выносливости стали при симметричном цикле изгиба;

k_σ=1,9–эффективный коэффициент концентрации нормальных напряжений;

ε_σ = 0,61 – масштабный фактор для нормальных напряжений;

σ_υ – амплитуда цикла нормальных напряжений

где М_max = 72 кНм – максимальный изгибающий момент в рассматриваемом сечении;

W – момент сопротивления сечения:

 

где τ_-1 = 220 МПа – предел выносливости стали при симметричном цикле кручения;

k_τ = 1,9 – эффективный коэффициент концентрации касательных напряжений;

ε_τ = 0,52 – масштабный фактор для касательных напряжений;

τ_υ – амплитуда цикла нормальных напряжений:

где М_max = 72 кНм – максимальный изгибающий момент в рассматриваемом сечении;

W_к – момент сопротивления сечения:

Запас прочности вала барабана удовлетворяет требованиям.

Прогиб вала:

4 ПРОВЕРОЧНЫЙ РАСЧЕТ ПРОЛЕТНЫХ БАЛОК КРАНА

 

Примем расчетные комбинации нагрузок для проектного расчета металлоконструкции моста:

• Комбинация нагрузок 1.1 .А.
• Комбинация нагрузок 1.1.Б.

Где римская цифра I означает предельное состояние конструкции, в нашем случае – прочность; арабская цифра 1 – расчетный случай положения тележки – в середине моста, буква – работа механизмов:

А – подъём грузов; Б – движение крана.

В качестве материала для несущих конструкций моста примем сталь как и у других элементов металлоконструкции сталь Ст3сп5 – 12 ГОСТ 380 – 71.

Расчетные сопротивления основного металла, в соответствии с таблицей 6.7 [3] равны:

При растяжении, сжатии, изгибе:

R = 260 (МПа).

При срезе R_cp = 15О (МПа).

При смятии торцевой поверхности R_m.см. = 390 (МПа).

Собственный вес моста крана при пролете 28,5 м равен

G =26·9,81= 255,1 (кН).

Интенсивность нормативной распределенной нагрузки на каждую балку моста определяем по формуле:

где G_пм.н – нормативный вес пролетной части моста (пролетной балки с площадками обслуживания), кН;

L – пролет крана, м;

 

4.1 Расчетные нагрузки комбинации 1.1. А

 

Расчетная схема приложения вертикальных нагрузок имеет вид рис. 6

Рисунок 6 – Расчетная схема приложения вертикальных нагрузок

где q_н – распределенная нагрузка от собственного веса пролетной части моста;

G_пр – вес приводов механизма передвижения крана;

G_к – вес кабины управления;

D₁, D₂ – давление колес тележки на балку;

D_R – равнодействующая давлений колес тележки;

При расчете будем использовать:

D₂ = 38,6 (кН);

D₁ = 50,8 (кН);

D_R = D₂ + D₁ = 89,4 (кН).

При четырехколесной тележке наибольший изгибающий момент от подвижной нагрузки действует в сечении под колесом с давлением , расположенным от опоры на расстоянии:

Большинство источников рекомендуют вводить в расчеты коэффициенты перегрузок:

Коэффициент перегрузки веса тележки принимают обычно:

К_а = 1,1 [3]

Исходя из вышеприведенного находим:

Нагрузка от собственного веса:

q = 1,1 · 4,475 = 4,9 ^кН/_м.

Вес кабины:

G_к = 21,5 · 1,2 = 25,8 кН.

Вес привода механизма передвижения

G_пр = 9,7 · 1,2 = 11,62 кН.

Равнодействующая давлений колес:

D_R = 89,4 · 1,3 = 116 кН.

Для сечения под колесом с давлением D₁ суммарный изгибающий момент равен:

где q – распределенная нагрузка от собственного веса пролетной части моста;

L – пролет крана;

D_R – равнодействующая давлений колес тележки;

G_np – вес привода механизма передвижения;

G_k – вес кабины управления;

Для расчетной схемы приложения вертикальных нагрузок, следующие значения имеют величины:

b₁ = 0,85 м; a₁ = 1,5 м; a₂ = 2,5 м.

Геометрические характеристики сечения пролетной балки моста по рисунку 7

Рисунок 7 – Геометрические характеристики сечения пролетной балки моста

Момент инерции относительно горизонтальной оси:

Момент инерции относительно вертикальной оси главной (пролетной) балки:

Момент сопротивления сечения пролетной балки относительно горизонтальной оси:

Момент сопротивления сечения пролетной балки относительно вертикальной оси:

Расчетная зависимость проверки прочности балки в средней части пролета имеет вид:

где М_1у – изгибающий момент в вертикальной плоскости;

W_x – момент сопротивления балки при изгибе в горизонтальной плоскости;

m₀ – коэффициент неполноты расчета;

R – расчетное сопротивление.

m₀ = m₁ ∙ m₂ ∙ m₃,(45)

где m₁ = 0,9 – коэффициент, учитывающий ответственность рассчитываемого элемента, т.е. возможные последствия его разрушения и наличие предупредительных признаков разрушения;

m₂ = 0,95 – коэффициент, учитывающий отклонения в геометрических размерах конструкции, влияние коррозии и т.п.;

m₃ = 0,85 – коэффициент, учитывающий несовершенство расчета, связанные с неточностью расчетных схем, неполнотой методов расчета и т.п.;

m₀ = 0,9 ∙ 0,95 ∙ 0,85 = 0,73;

Расчетная прочность балки:

σ = 115,4 < 0,73 · 260

σ = 115,4 (МПа) < 189,9 (МПа);

Прочность средней части пролетной балки при изгибе в вертикальной плоскости обеспечена [3].

 

4.2 Расчетные нагрузки комбинации 1.1. Б

 

Расчетная схема приложения нагрузок в вертикальной плоскости аналогична схеме при комбинации нагрузок 1.1. А.

Вертикальные динамические нагрузки, возникающие при движении крана определяют по выражению:

где h_с = 3-15 мм – высота ступеньки стыка рельсов;

а = 0,025 – коэффициент, принимаемый в зависимости от скорости крана V_k, ^м/_сек и частоты колебания моста;

ξ – коэффициент, зависящий от схемы крана и вида нагрузки;

Для собственного веса моста двухбалочного четырехколесного крана коэффициент будет равен:

где В_к – база крана;

L_T – колея тележки;

Парциальная частота собственных поперечных колебаний моста определяется по формуле:

где С_м – коэффициент жесткости, ^кН/_м ;

m_т – приведенная масса моста, т;

Коэффициент жесткости моста может быть принят как минимально возможный по условиям третьего предельного состояния.

где G_q.н. – номинальный вес груза, кН;

G_т.н. – номинальный вес тележки, кН;

L – пролет крана, м;

[f_<] = ¹/₆₀₀ – предельный относительный прогиб моста при действии номинальной подвижной нагрузки принимаемый в соответствии с ОСТ – 24.090.72 – 83.

Определяем изгибающий момент для сечения под колесом с давление D₁:

Горизонтальные нагрузки двухбалочного моста.

Влиянием горизонтальных нагрузок от инерции масс приводов механизма передвижения и кабины при расчетах можно пренебречь.

Схема приложения горизонтальных нагрузок от инерции масс комбинации 1.1. Б. при четырехколесной тележке имеет вид на рисунке 8:

Рисунок 8 – Схема приложения горизонтальных нагрузок.

С достаточной степенью точности суммарный горизонтальный изгибающий момент в расчетном сечении пролета может быть определен по выражению:

где q_г – горизонтальная нагрузка от распределенного веса пролетной части моста;

L – пролет крана;

D_Rг – равнодействующая горизонтальных давлений колес тележки;

Величину находим по формуле:

где В_к – база крана, м;

J_1y – момент инерции пролетной балки относительно вертикальной оси;

J_2y – момент инерции концевой балки относительно вертикальной оси;

L_т – колея тележки;

Геометрические характеристики сечения концевой балки моста по рисунке 9

Рисунок 9 – Геометрические характеристики сечения концевой балки моста

Момент инерции относительно горизонтальной оси:

Момент инерции относительно вертикальной оси концевой балки:

Момент сопротивления сечения пролетной балки относительно горизонтальной оси:

Момент сопротивления сечения концевой балки относительно вертикальной оси:

Тогда:

При J_k = 0,1 (^м/_сек²) – ускорение, возникающее в период неустановившегося режима работы механизма передвижения, т.е. при , горизонтальные инерционные нагрузки будут равны:

Тогда суммарный изгибающий момент в горизонтальной плоскости:

m₃ принимаем равным 0,95, тогда коэффициент неполноты расчета будет равным:

m₀ = 0,9 ∙ 0,95 ∙ 0,95 = 0,812.

Проверку прочности балки в средней части пролета при действии нагрузок комбинации 1.1. Б производим по следующей зависимости:

где М_1у – изгибающий момент в вертикальной плоскости;

М_1х – изгибающий момент в вертикальной плоскости;

W_x – момент сопротивления балки при изгибе в горизонтальной плоскости;

W_у – момент сопротивления балки при изгибе в вертикальной плоскости;

m₀ – коэффициент неполноты расчета;

R – расчетное сопротивление материала моста.

σ = 112,92 (МПа) < 211 (МПа).

Прочность средней части балки при изгибе в двух плоскостях обеспечена.

 

4.3 Прочность верхнего пояса балки моста

 

При контакте подошвы рельса с поясом балки, пояс находится в плосконапряженном состоянии и его прочность нужно проверять по условию:

где σ_z = σ_z0 + σ_z.м.;

σ_z0 – напряжение в балке от ее общего изгиба в продольном направлении;

σ_z.м и σ_у.м – местные нормальные напряжения в поясе соответственно вдоль и поперек продольной оси балки;

где N – сила, передающаяся на поясной лист через рельс от давления ходового колеса тележки;

где δ_п – толщина пояса;

k₂ и k₃ – коэффициенты;

а₁ – расстояние между диафрагмами;

J_p.c – момент инерции рельса в вертикальной плоскости;

D – давление от колес тележки;

При а₁ = 835 мм, b = 480 мм определяем:

k₁ = 0,149; k₂ = 0,25; k₃ = 0,18;

тогда:

где М₁ – изгибающий момент в вертикальной плоскости определенный для нагрузок комбинации 1.1. Б;

W_1х – момент сопротивления балки при изгибе в горизонтальной плоскости;

σ_z = 103,8 + 7,52 = 111,32 (МПа).

112,9 (МПа) < 166,4 (МПа).

 

4.4 Торцевая балка моста крана

 

Проверку прочности балки в опасном сечении – в узле сопряжения с пролетной балкой – производим для случая действия нагрузок комбинации 1.2. Б (тележка у торцевой балки).

Расчетная схема нагружения моста крана на рисунке 10:

Рисунок 10 – Расчетная схема нагружения моста крана

G_пр – вес приводов механизма передвижения крана;

G – вес пролетной балки;

D₁, D₂ – давление колес тележки на рельс;

Определим более опасное с точки зрения максимальной поперечной силы в опорном сечении положения тележки.

При положении тележки с грузом у опоры А реакция опор “приводной” пролетной балки определяется согласно указанной выше схемы.

При положении тележки с грузом у опоры В:

Более опасным будет случай положения тележки у опоры В.

Горизонтальные изгибающие моменты в узлах сопряжения балок:

У более нагруженной концевой балки этот момент равен:

где L – пролет крана, м;

L_T – колея тележки, м;

q_г – горизонтальная нагрузка от распределенного веса пролетной части моста;

D_1г – горизонтальная нагрузка от силы давления колеса;

Р_пер – сила перекоса при движении крана;

где В_к = 5,3 м – база крана;

где J_1y – момент инерции пролетной балки относительно вертикальной оси;

J_2y – момент инерции концевой балки относительно вертикальной оси;

Сила перекоса при движении крана:

где μ_сц – коэффициент сцепления приводных колес с рельсами (при работе в помещении μ_сц = 0,2);

суммарное давление на приводные колеса менее нагруженной концевой балки;

тогда:

Скручивающий момент для опорного узла приводной пролетной балки:

где q_iг – распределение нагрузки;

Р_i – сосредоточенные нагрузки;

L – пролет балки;

z_i – расстояние от рассматриваемого опорного сечения;

_i – эксцентриситеты нагрузок относительно Ц.И.;

Т_пр – реактивный момент привода передаваемый на балку;

Схема нагрузок на приводную балку для определения скручивающих нагрузок приведена на рисунке 11

Рисунок 11 – Схема нагрузок на приводную балку для определения скручивающих нагрузок

Для неприводной пролетной балки:

Максимальный изгибающий момент в вертикальной плоскости:

Горизонтальный момент равен М_г = 132,21 (кНм);

Определим нормальные напряжения изгиба в двух плоскостях:

принимаем m₀ =0,9; R_p = 0,9 ∙ 260 = 234 (МПа).

σ = 122,7 (МПа) < 234 (МПа).

Максимальные касательные напряжения среза в стенке:

τ = 23,4 (МПа) <  = 135 (МПа).

Прочность торцевой балки обеспечена. [3]

---

1  2  3