Вид работы: Лабораторная работа
Предмет: Основы преобразования информации
Тема: Технология полиграфического и упаковочного производства
Лабораторная работа №2. ВШПиМ МПУ
Размытие при воспроизведении изобразительной информации.
Взаимосвязь различных функций, описывающих размытие.
К числу практически важных задач относится расчет распределения интенсивности в изображении одиночной (отдельной) мелкой штриховой детали, воспроизводимой в системе с размытием.
Непосредственное применение функции передачи модуляции (ФПМ) или расчет воспроизведения в соответствии с интегральными преобразованиями по прямой теореме свертки в данном случае являются достаточно трудоемкими. Более просто и наглядно эта задача решается с использованием краевой функции (КФ). Таким образом, возникает необходимость в преобразовании ФПМ в КФ.
С другой стороны, в ряде случаев при исследовании системы или ее отдельных звеньев бывает невозможным размещение в объекте периодического тест-объекта, но в то же время в самом объекте имеются отдельные детали с резкими краями. Анализ таких деталей позволяет получить КФ. Следовательно, тогда для оценки передаточных свойств возникает необходимость в решении обратной задачи — переходе от КФ к ФПМ.
При отображении изобразительной информации мы сталкиваемся с проблемой точной передачи мелких деталей.
Реальные системы отображения информации обычно обладают некоторым размытием, которое проявляется в том, что бесконечно большой импульс, приложенный на бесконечно малом пространстве (или на бесконечно малом отрезке времени) и называемый -функцией (дельта-функцией), воспроизводится системой уже не в виде -функции, а характерным для данной системы (ее отдельного звена) пятном размытия.
Поскольку реальные системы отображения (носители) информации обладают размытием, то исходные функции (край полуплоскости, бесконечно узкая цель и т.д.) будут отображаться с искажениями их начальной формы. Этим исходным сигналам будут соответствовать распределения интенсивности, дающие информацию о размытии:
1) краевая функция (КФ), h(x), описывающая распределение интенсивности в изображении края полуплоскости
функция размытия линии (ФРЛ), g(х), описывающая распределение интенсивности в изображении бесконечно узкой щели.
Одномерная дельта-функция ( (x) и функция размытия линии g(x)).
Краевая функция и функция размытия линии взаимосвязаны, и одна может быть найдена из другой.
Выполнение работы
Задано:
- формула для построения ФРЛ
- параметр
Функция g(x) является симметричной относительно оси ординат, поэтому необходимо только нормировать эту функцию.
gmax(x) = 1, это реализуется умножением функции на некоторый множитель.
Нахождение множителя:
При x = 0 функция g(x) = 0,399.
Нам необходимо значение при х = 0 g(x) = 1.
Тогда и функция станет нормированной:
Построим ФРЛ на отрезке [- 3, 3] мкм.
Зону размытия ФРЛ [- x0, x0] разделим на n = 24 частей через интервал 0,25.
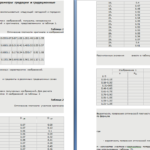
По формуле для точек деления найдем значения g(x). Полученные результаты сведем в таблицу, учитывая симметричность функции относительно оси ординат.
Используя полученные значения, строим график функции размытия линии.
Краевая функция и функция размытия линии взаимосвязаны, и одна может быть найдена из другой.
Краевая функция рассчитывается посредством интегрирования функции размытия линии:
Где x0 – начало зоны перехода, xi – текущее значение x внутри зоны перехода [-x0, x0].
Функция размытия линии находится по краевой функции:
КФ как и ФРЛ нормируется:
При х=3 функция h(x) должна равняться 1, а при x=0 h(x)=0,5.
КФ нормируется аналогично ФРЛ и в результате получаем нормированную КФ:
По найденным точкам для ФРЛ по формуле трапеции находим значения интеграла:
Где найденный коэффициент нормализации 0,165.
Полученные результаты заносим в таблицу и находим значения h(x) и строим график краевой функции.
Вывод:
В ходе работы провели исследование взаимосвязи различных функций, описывающих размытие, а также выполнили расчет и построение краевой функции.
Прикрепленные файлы:
Прикрепленные файлы: |
|
|---|---|

|
Администрация сайта не рекомендует использовать бесплатные работы для сдачи преподавателю. Эти работы могут не пройти проверку на уникальность. Узнайте стоимость уникальной работы, заполните форму ниже: Узнать стоимость |

|
Скачать файлы: |
|
|
|