ТЕСТОВЫЕ ЗАДАЧИ И УПРАЖНЕНИЯ КАК СРЕДСТВО ПОВТОРЕНИЯ ТЕМЫ ВЕКТОРЫ

ВВЕДЕНИЕ

ГЛАВА 1 ТЕОРЕТИЧЕСКИЙ И МЕТОДИЧЕСКИЙ ПОДХОДЫ К

ИЗУЧЕНИЮ ОСНОВ ВЕКТОРНОГО ИСЧИСЛЕНИЯ

История развития векторного исчисления

1.2. Векторное исчисление в курсе математики. Различные подходы к

определению понятия вектора

1.3. Анализ учебной литературы

1.4. Изучение векторного метода в средней школе

ГЛАВА 2 ВЕКТОРНЫЙ МЕТОД В РЕШЕНИИ ЗАДАЧ И

ДОКАЗАТЕЛЬСТВА УТВЕРЖДЕНИЙ

2.1. Основные типы задач, решаемые векторным методом

2.2. Доказательство алгебраических и геометрических неравенств, с

применением скалярного произведения

2.3. Тестовые задания по переводу геометрического содержания задачи на

векторный язык

ГЛАВА 3 ВЕКТОРНЫЙ МЕТОД В ЗАДАЧАХ ИТОГОВОЙ АТТЕСТАЦИИ

3.1. Задачи на нахождение угла, решаемые векторным методом в открытых

банках заданий

3.2. Задачи на нахождение расстояний, решаемые векторным методом в

открытых банках заданий

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ И ИСТОЧНИКОВ

ВВЕДЕНИЕ

 

Вектор является одним из основных математических понятий. При помощи векторного метода эффективно решаются различные задачи курса планиметрии и стереометрии. Применяемые в рамках евклидовой геометрии векторные методы значительно упрощают доказательства многих теорем и решение задач. Например, доказательства теоремы косинусов, теоремы о трех перпендикулярах и других стали значительно проще при применении скалярного произведениях векторов. Но роль векторов – не только в упрощении трудных мест школьного курса. Гораздо важнее то, что векторные методы находят сейчас широкое применение в физике, химии, экономике, биологии, не говоря уже о многих разделах современной математики. Так, скалярное произведение вектора силы и вектора перемещения есть работа, векторное произведение вектора тока и вектора напряженности магнитного поля есть сила воздействия этого поля на проводник и т. д. И здесь геометрия диктовала физике введение новых понятий, а не наоборот. А впоследствии, при рассмотрении многомерных пространств, скалярное произведение приобрело ещё больший вес и значение и стало важным рабочим аппаратом, применяемым буквально во всех областях математики и ее приложений. Кроме того, сам курс векторного исчисления в школе, является подготовительным этапом его дальнейшего развития и изучения на более глубоком уровне для большинства различных  предметов в области высшего профессионального образования.

В настоящее время в практике преподавания сложилась ситуация, которая свидетельствует о сохраняющихся системных недостатках в преподавании геометрии. Геометрическая задача 14 в Едином Государственном Экзамене  (стереометрия) повышенного уровня сложности имеет низкий процент выполнения (средний процент выполнения – 2,5), что свидетельствует о несформированности у большинства выпускников умения строить изображения многогранников и сечения многогранников плоскостями, комбинировать различные методы решения задач с использованием свойств фигур, пользоваться векторами и координатами для решения задач. Пути исправления ситуации видятся в полноценном изучении геометрии. Это обуславливает актуальность тематики выпускной квалификационной работы.

Объект исследования – изучение  геометрии в старших классах общеобразовательной школы;

Предмет исследования – задачи и упражнения, позволяющие повторить тему «Векторы» и актуализировать использование векторных методов в решении геометрических задач.

Целью работы является выявление условий эффективного обучения учащихся векторному методу и разработка тестовых задач и упражнений для повторения темы «Векторы»

Для достижения указанной цели в работе последовательно решается ряд задач:

В первой главе, которая носит подготовительный характер, рассмотрены различные подходы к определению понятия вектора, история формирования данного понятия в контексте развития различных разделов естествознания и математического образования. В частности затронут подход Вейля к аксиоматическому построению геометрии  на основе понятия вектора, который, как показывает анализ учебной литературы, является основополагающим при построении практически всех наиболее распространенных учебных пособий. Это комплекты учебников геометрии Атанасян Л.С., Бутузова В.Ф., Кадомцева С.Б. и др. Геометрия 7-11 классы, Погорелова А.В.  Геометрия 7-11 классы, А.Д. Александрова, А.Л. Вернер, В.И. Рыжика. Геометрия 7-11. Анализ темы в представленных учебниках позволили выявить общие принципы построения методики и ее различия у разных авторов, что позволило определить цели изучения векторного метода в средней школе. К ним относят…

Анализ решения задач векторным методом, позволил сформулировать в работе основные компоненты векторного метода решения задач и понятийного аппарата, которым должен овладеть ученик, чтобы решать задачи векторным методом.

Вторая глава посвящена изучению векторного метода в решении задач и доказательствах утверждений. В ней рассмотрены два основных типа геометрических задач аффинных и метрических, в решении которых целесообразно применение векторного метода. Задачу называют аффинной, если она не связана с измерением отрезков и углов  (прямо или косвенно). В противном случае задачу называют метрической или евклидовой. Среди них имеются задачи на доказательство и на вычисление, планиметрические и стереометрические. В задачах с аффинным содержанием обычно требуется установить принадлежность трёх точек одной прямой или четырёх точек одной плоскости, вычислить отношение, в котором точка, принадлежащая отрезку, делит этот отрезок, доказать параллельность отрезков или прямых, сонаправленность или противоположную направленность лучей, параллельность прямых и плоскостей. Реже встречаются задачи на нахождение различных множеств точек. В метрических же задачах преимущественно приходится вычислять расстояния и углы (междупрямыми, прямой и плоскостью, двугранные углы), доказывать перпендикулярность прямых и плоскостей и значительно реже находить и изучать множества точек на плоскости и в пространстве.  Решению этих задач посвящена большая часть второй главы. Опыт показывает, что самое трудное для учащихся – это научиться делать перевод геометрического факта на язык векторов и обратный перевод.

Чтобы сформировать у учеников умение переводить текст задачи на векторный язык, следует отработать сначала перевод отдельных элементов текста задачи и их связей на векторный язык, а уж затем чтение векторных соотношений. Для выработки отмеченных навыков в работе составлен ряд базовых тестовых заданий и упражнений, решение которых позволяет закрепить навык перевода основных геометрических понятий на язык векторов и находить геометрические интерпретации векторных выражений. Эти задания систематизируют знания учеников по векторной алгебре, помогает правильно выбрать векторы, которые удобно использовать для решения задачи, а также помогает записать условие задачи с помощью выбранных векторов и сделать соответствующие выводы и обобщения по мере выявления зависимости между ними. Кроме этого в заключительной части работы рассмотрены все основные типы задач, встречающиеся в  открытом банке заданий, решение которых рационально векторным методом. Это задачи по нахождению угла между прямыми, угла между прямой и плоскостью, угла между плоскостями; задачи на вычисление расстояния от точки до плоскости и расстояния между скрещивающимися прямыми. Следует отметить, что последние задачи относятся к заданиям профильного уровня и требуют от учащихся владения векторным методом на достаточно высоком уровне.

 

ГЛАВА 1. ТЕОРЕТИЧЕСКИЙ И МЕТОДИЧЕСКИЙ ПОДХОДЫ К ИЗУЧЕНИЮ ОСНОВ ВЕКТОРНОГО ИСЧИСЛЕНИЯ

1.1 История развития векторного исчисления.

 

Несмотря на то, что векторное исчисление в современном виде сформировалось в середине 19в., его истоки лежат в далеком прошлом. В Древней Греции математики пытались найти решение многих задач алгебры и арифметики геометрическим путем. В работе Евклида «Начала»,  алгебраические операции сложения и умножения интерпретировались как сложение отрезков и построение на них прямоугольников. Была  заложена  геометрическая теория отношений Евдокса. Вместе с этим, сам термин «сложения движений», был уже сформулирован механиками и астрономами и применялся в работах Архимеда и Птолемея. В 16 веке фламандец  С. Стевин публикует трактат «Основы статики», в котором  впервые применяет правило параллелограмма для сложения сил и использует для их обозначения стрелки. Позже, в 17 веке, Валлис в «Механике» использует правила,  в точности, совпадающие с правилами параллелограмма и параллелепипеда. С их помощью автор складывает различные физические величины. Астроном Кеплер,  при формулировке своих законов движения планет использует направленный отрезок с центром в Солнце и концом, направленным к движущемуся телу. Однако говорить о формировании векторной величины в то время было еще рано. Дальнейшее развитие векторное направление  получило  уже в алгебраической сфере и  связано с трудами датского землемера  ГаспараВесселя,  который в 1797 году представил академии наук в Копенгагене свой труд «О геометрической интерпретации комплексных чисел». Именно ему приписывают первое представление комплексных чисел, как направленных отрезков, введению операций умножения и деления при помощи их записи в тригонометрической форме. Вессель вводит правила сложения направленных отрезков на плоскости и в пространстве, развивая «алгебру вращения сферы», для решения задач по отысканию элементов сферических треугольников и многоугольников. Таким образом, развитие элементов векторного исчисления послужило решению прикладных задач, связанных с геодезией.  Представление комплексных чисел в виде направленных отрезков, использованное вначале Весселем, а в последствии Гауссом,  давало возможность их плодотворного применения в решении двумерных задач планиметрии и математической физики. Позднее английские математики Д.  Пикок, Д. Грегори, А. Де Морган, У. Гамильтон предпринимали попытки обобщить теорию комплексных чисел, на случай трех измерений, изучая вначале триплеты — выражения видаа затем, не добившись успеха и кватернионы

«Лекции о кватернионах» 1843г. Гамильтона явились основным алгебраическим источником современного векторного исчисления. В этой работе впервые вводится термины «вектор», «скаляр», «скалярное произведение», «векторное произведение» и изучены операции над векторами в пространстве. Именно теория кватернионов, развитая впоследствии  П. Тетом, дала возможность использовать аппарат векторного исчисления в аналитической геометрии. «Элементарный трактат по теории кватернионов» содержит главу «Геометрия прямой и плоскости» в которой сформулированы и решены базовые задачи аналитической геометрии, которые и по сегодняшний день входят в учебники. Окончательное становление векторного исчисление произошло во второй  половине 19 века и связано с именами Д. Максвелла и Г. Грассмана, которые явились предшественниками синтеза физического, алгебраического и геометрического  направлений, в развитии векторного исчисления и оформлении его в независимый раздел математики.

В настоящее время действия с векторами изучает раздел именуемый векторной алгеброй, наряду с ним существует, созданный Гамильтоном векторный анализ, изучающие вектор-функции.

Векторное исчисление, возникшее из решения прикладных задач в геодезии, астрономии и механике, в настоящее время используется практически во всех разделах математики, физики и других наук, подчеркивая тесную связь между ними,  и является одним из краеугольных камней всего естествознания.

 

1.2. Векторное исчисление в курсе математики. Различные подходы к определению понятия вектора.

Рассмотрим основные подходы к определению вектора, встречающиеся в различных учебных курсах

Абстрактный — представлен,   в «Курсе аналитической геометрии и алгебры»  Д.В. Беклемишева [3]. Вектор определяется, посредством описания свойств операций сложения и умножения на число, которые более чем-либо другим не определены.

Определение. Вектор — элемент пространства V, произвольной природы с введенными на нем операциями сложения элементов и умножения элемента на действительное число, такими, что указанные операции удовлетворяют требованиям 8 аксиом:

 

В данном случае определение вводится аксиоматически. После чего приводятся примеры таких векторных пространств, таких как — множество направленных отрезков на плоскости.- множество комплексных чисел над R.

Алгебраический – реализуется в учебнике Л.Я. Куликова «Алгебра и теория чисел» [4]:

Определение. n—мерным вектором над полем  F называется любой кортеж из n – элементов поля  F. Обозначается в виде .

Вводятся определения равных векторов, сложения векторов и умножения вектора на число.

Определение. Векторы и называют равными, если ;

Определение. Суммой векторов и называют вектор

.

Определение. Произведением скаляра на вектор называют вектор

.

Определение. Вектор — называют нулевым.

Определение. Вектор называют противоположным вектору .

Этот подход является в большей мере алгебраическим и сводит действия над объектами к операциям над числами.

Наряду с этими подходами к определению вектора,  существуют различные геометрические интерпретации вектора,  согласно которым «вектор это геометрический объект, характеризующийся направлением и длиной».

Традиционный

Вектор понимается как множество сонаправленных  отрезков, имеющих одинаковую длину. Под длиной вектора понимают длину отрезка, который его представляет. Векторы рассматривают с точностью до их параллельного переноса, и называют свободными. Равные векторы, не совпадающие по положению, рассматриваются как различные конкретные изображения одного и того же свободного вектора.

Данный подход реализуется во многих учебных пособиях и имеет ряд преимуществ. Он упрощает понятия равенства, однозначно определяет операции для свободных векторов, но, тем не менее, осложняется некоторыми нюансами. Примером может служить изображение силы, как физической величины в виде направленного отрезка, однако она не может быть изображена вектором в смысле этого определения, поскольку силы, изображаемые равными направленными отрезками, производят различные действия. (Если сила действует на упругое тело, то отрезок ее изображающий,  не может быть перенесен по прямой)

Вектор, как параллельный перенос

Параллельным  переносом называют такое движение в пространстве,  при котором точки смещаются по параллельным прямым на одно и то же расстояние в одном и том же направлении.  При данном подходе вектор определен  как, параллельный перенос плоскости. Это  позволяет устранить противоречия между понятиями равенства и эквивалентности, присутствующее в традиционном определении вектора, как направленного отрезка и определяет  логически строгое изложение векторного исчисления. Однако он лишен наглядности.

Вектор, как направленный отрезок

Чаще всего встречается в изложении курса геометрии.  Фундамент понятия  составляют следующие определения:

Определение. Пара точек, для которых указано, какая из них первая, а какая вторая, называется упорядоченной.

Определение. Отрезок, концы которого упорядочены, называется вектором.

Определение. Расстояние между началом и концом отрезка называют его длиной.

Определение. Векторы называются коллинеарными, если они параллельны одной прямой.

Определение. Векторы называются сонаправленными, если  а) они лежат на параллельных прямых;

б) лежат в одной полуплоскости относительно прямой .

Если условие а) выполняется, а б) не выполнено, то векторы называют противоположно направленными

 

Определение. Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют равные длины.

Определение. Суммой векторов и называют вектор, построенный на и по правилу треугольника или правилу параллелограмма.

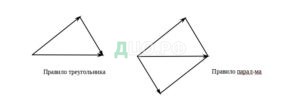
Рис.1.1Правила сложения векторов

Определение. Произведением вектора на действительное число называется вектор

такой, что  а) ;

б) или   .

Данный подход к определению вектора обладает достаточно высоким уровнем наглядности, но определяет результат действий над векторами с достаточно большим произволом.

 

Подход Вейля  к определению вектора.

На фоне всех уже перечисленных подходов к определению понятия вектора нельзя оставить в стороне еще один, отличный от всех остальных, подход

Вейля, послуживший отправной точкой создания целой аксиоматики.

Идея Вейля состояла в том, чтобы принять в качестве неопределяемых понятий точку и вектор, а в качестве аксиом — свойства сложения векторов и умножения вектора на число. А именно, согласно аксиоматике Вейля, операция сложения векторов должны удовлетворять требованиям группы аксиом

Кроме этих групп Вейль вводит группу аксиом размерности, группу аксиом скалярного умножения, а в последней 5 группе рассматривает аксиомы точек – свойства, устанавливающие связь между неопределяемыми понятиями вектора и точки.

 

Такой подход имеет ряд преимуществ. «С формальной стороны это лишь один из возможных путей аксиоматизации геометрии, эквивалентный гильбертовскому, т. е. позволяющий доказать те же самые теоремы. Но с методологической точки зрения вейлевский путь является неизмеримо более ценным. Вместо скрупулезной, утомительной и длинной цепочки рассуждений по гильбертовской схеме (к тому же оторванной от других разделов математики и от естественных наук) вейлевская схема дает исключительно ясное и краткое изложение, насыщенное современными идеями и близкое к наиболее актуальным разделам математики, физики, экономики и других областей знания» [6]

1.3.  Анализ учебной литературы.

Тема «Векторы» появляется  в курсе математики тогда еще советского школьного образования в 1963 году.  Вопрос о ее присутствии и значимости темы практически не возникал.   Вектор  является одним из фундаментальных понятий математики и  присутствие в школьном курсе векторного метода позволяет, во-первых, упростить решение многих задач, которые другими методами решаются труднее, внести в доказательства теорем и решение задач элемент наглядности, сделать приобретение геометрических знаний более естественным и доступным. Во-вторых, понятие вектора востребовано в изучении школьного курса физики и астрономии, что играет существенную роль в межпредметных связях. И в-третьих дает возможность заложить основы многих понятий, связанных с векторным исчислением и его применением во многих приложениях математики. Несмотря на то внимание, которое уделяется теме «Векторы», она была и остается наиболее трудной темой как для восприятия учащимися, так и для методики преподавания.  Сложность  темы подчеркивают исследования таких математиков, как А.Д. Александров, Л.С. Атанасян, В.А. Погорелов, А.Н. Колмогоров и многих других. Изучению методики преподавания темы «Векторы» в школьном курсе геометрии посвящено много работ. Их анализ позволяет сформулировать те моменты, которые вызывают у учащихся наибольшие затруднения:[2]

-способ введения понятия вектора;

-свойства сложения векторов и умножения вектора на число, скалярного умножения векторов;

-доказательства теорем, использующие переместительный и сочетательный законы  сложения векторов, теоремы о выражении скалярного произведения векторов через координаты.

Эти трудности представляют те противоречия, которые возникает между необходимостью обучения учащихся векторному методу, и его практической реализацией. Остановимся на них более подробно, анализируя, различные школьные учебные пособия.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7-11 классы

Тема «Векторы» впервые рассматривается в 8 классе и ему отведена 9 глава, состоящая из 3 параграфов.

• 1. Понятие вектора

Понятие вектора вводится на основе уже встречавшихся в курсе физики у учеников векторных величин. В качестве такого примера здесь выступает сила. Далее авторы, отвлекаясь от конкретных физических свойств, переходит к геометрическому понятию вектора. Вектор или направленный отрезок определен, как отрезок, «для которого указано, какая из его точек является началом, а какая — концом» После этого вводится условие считать точку нулевым вектором,  и определяется  длина или модуль вектора, как длина отрезка, который его представляет.  Второй пункт §1 дает определение  равных векторов.  Для этого авторы вновь обращаются к примеру движения тела, в котором все его точки движутся с одной и той же скоростью в одном и том же направлении. Указывая на то, что скорость является векторной величиной, а она изображается направленным отрезком, делается вывод о том, как определить равенство векторов. Рассмотрев дополнительно условие коллинеарности и сонаправленности векторов, в этом пункте дается определение равных векторов, как сонаправленных векторов одной длины. Заключительный пункт этого параграфа посвящен откладыванию вектора от данной точки. В нем доказывается утверждение, того, что от любой точки может быть отложен вектор равный данному и притом только один. Доказательство единственности опирается на построение, как и все предыдущие рассуждения. Также в конце параграфа присутствуют практические упражнения, направленные на закрепление введенных понятий и их свойств.

• 2. Сложение и вычитание векторов.

Посвящен сумме и разности векторов. Как и прежде, на примере перемещения материальной точки из точки в , а затем из в , делается вывод об их сумме,  как сумме направленных отрезков. Полученное правило суммирования оформляется, как правило треугольника. С его помощью доказываются переместительный и сочетательный закон сложения векторов:

Для любых векторов справедливы равенства:

-переместительный закон;

-сочетательный закон.

В процессе доказательства обосновывается правило параллелограмма, которое также используется при сложении векторов. Правила треугольника и параллелограмма обобщаются на случай сложения произвольного числа

векторов. Их сумма определяется по правилу многоугольника.

 

Рис.1.2. Правило многоугольника

Разность векторов определяется, как вектор, сумма которого с вектором дает вектор . Здесь же определяется противоположный вектор. Практические задания содержат задачи на применение правил суммирования векторов и нахождения их разности. Вопросы и задачи содержат задания на доказательство неравенств, в которых фигурируют модуль суммы  и разности векторов. Также присутствуют задачи на выражение одних векторов через другие.

• 3. Умножение вектора на число. Применение векторов к решению задач.

В этом параграфе авторы по сложившейся традиции рассматривают операцию умножения вектора на число на примере такой физической величины, как скорость трех автомобилей. Она в данном примере имеет одно и то же направление, но отличается по модулю.  Пример, как и в предыдущих случаях, наводит на правило умножение векторов на число.

Произведением ненулевого вектора на число называется такой вектор , длина которого равна , причем и .

Доказываются, свойства операции умножения вектора на число.

Для любых векторов , и любых чисел справедливы равенства:

— сочетательный закон;

— первый распределительный закон;

второй распределительный закон.

Этот параграф содержит достаточно большое количество задач, которые могут решаться при помощи векторов. Доказанным примером такого применения служит теорема о средней линии трапеции. Здесь же собраны задания повышенной трудности.

 

Учебный материал для 9 класса начинается с главы 10 «Метод координат»

• 1 Координаты векторовначинается с доказательства леммы о коллинеарных векторах:

Если векторы и коллинеарны и , то существует такое число , что .

Доказывается теорема о разложении любого вектора по двум неколлинеарным векторам и его единственности. Вводятся координатные векторы . Они используются в уже доказанной теореме, в качестве неколлинеарных векторов, по которым производится разложение. Речь идет фактически о введения базиса на плоскости, хотя понятия линейной зависимости и независимости векторов в явном виде нет. Координаты вектора определяются классическим способом, как коэффициенты разложения вектора по.

На основе этого определения координат в пункте 87 доказываются свойства о координатах суммы, разности векторов и произведение вектора на число. В §2 рассматривается связь между координатами вектора и координатами точек, его образующих. Вводится в рассмотрение понятие радиус-вектора точки и доказывается, что координаты точки совпадают с координатами радиус-вектора. В пункте 89 решаются простейшие вспомогательные задачи в координатах: нахождение середины отрезка, вычисление длины вектора по его координатам, и задача о вычислении расстояния между двумя точками. Завершает эту главу §3 Уравнение окружности и прямой и задачи связанные с ними. В Главе 11 «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов» после определения основных тригонометрических функций угла и соотношений в треугольнике, авторы определяют скалярное произведение векторов.

Скалярное произведение векторов, есть произведение их длин на косинус угла между ними. . После вывода отношения

рассматривается выражение скалярного произведения в координатах: В прямоугольной системе координат скалярное произведение векторов и выражается формулой . Завершает векторную тематику изучение свойств скалярного произведения и применение скалярного произведения к решению задач. Следующим этапом в изучении векторов в курсе геометрии, представленным данным учебным пособием является изучение векторов в пространстве, которое начинается с одноименной главы и рассматривается в 10 классе. Структура материала повторяет изучение векторов на плоскости. Дополнительно вводится понятие компланарных векторов, правило параллелограмма обобщается правилом параллелепипеда, и в 45 пункте рассматривается разложение вектора по трем некомпланарным векторам. Метод координат, изучаемый в главе 5,  методически повторяет аналогичный материал для плоскости, с тем отличием, что задачи решаются в трехмерном пространстве. Скалярное произведение используется  для вывода уравнения плоскости. Таким образом, весь материал, представленный в данном пособии, можно представить в виде следующей таблицы.

Таблица 1.Распределение учебного материала в учебнике Л.С. Атанасяна

Вывод: Тема «Векторы», в одном из самых распространенном учебном пособии по геометрии опирается на модель, в которой вектор представляет собой направленный отрезок. Изложение материала проводится по направлению, которое задается  аксиоматикой Вейля. Выбранная модель, обладает высокой степенью наглядности, соотносится с задачами из курса физики и удовлетворяет основным потребностям в геометрических знаниях у школьников. К недостаткам следует отнести нарушение математической строгости изложения материала, по сути, модель заменяет математическое понятие и как следствие не предполагает других представителей векторных пространств, кроме направленных отрезков.  Отношение равенства заменяет отношение эквивалентности, которое является более актуальным при определении вектора, как класса эквивалентности. Определение суммы в явном виде отсутствует, его заменяет правило построения суммы векторов. Очевидны большие затраты времени на изучение темы.

Погорелов А.В.  Геометрия 7-11 классы

Изложение материала начинается в 8 классе с 10 параграфа. Вектор  определен как направленный отрезок и обозначается либо как самостоятельный элемент , либо посредством задания двух точек . Сразу вводится понятие сонаправленных и противоположно направленных векторов, абсолютная величина или модуль и нулевой вектор. Равенство векторов определено посредством их совмещения параллельным переносом. В пункте 93 [9] определяются координаты вектора как разности координат начала и конца. Таким образом, использую связь с формулой расстояния между двумя точками, автор сразу получает формулу для вычисления модуля вектора. Сложение векторов определено в пункте 94 как вектор с суммой координат. Доказывается теорема«Каковы бы ни были точки , имеет место векторное равенство ». Именно она дает возможность наглядно представить правило суммы векторов в виде правила треугольников и правила параллелограмма. 95 пункт «Сложение сил» описывает возможность разложения вектора, по его проекциям на оси, в том числе и перпендикулярные друг другу. Умножение вектора на число определяется также посредством координат с приданием ему геометрического смысла в виде доказанной теоремы. В пункте 97  дается определение коллинеарных векторов, как лежащих на одной или параллельных прямых и доказывается, что любой вектор плоскости может быть представлен в виде линейной комбинации двух неколлинеарных векторов. Заключительные два пункта 98 и 99 посвящены заданию операции скалярного умножения, как суммы произведений соответствующих координат, определению угла между векторами и разложению вектора  по координатным осям, при помощи ортов.  К теме «Векторы в пространстве» автор обращается в 10 классе.  Изложение материала проводится в той же последовательности, как и для векторов на плоскости, с учетом добавления еще одной координаты. В 37 пункте вводится понятие компланарных векторов. И доказывается теорема о разложении произвольного вектора по трем некомпланарным векторам. План изложения дает следующая таблица:

 

Таблица 2.Распределение учебного материала в учебнике А.В. Погорелова

 

Вывод:  В рассмотренном учебном пособии, вектор также представляет направленный отрезок. Сумма и произведение вектора на число определяются посредством координат. Это определения являются математически строгими, позволяют значительно сэкономить время изложения так, как идет изучение двух тем в одной, однако они лишены наглядности, как элемента, который помогает изучению данной темы. Кроме этого, к недостаткам изложения можно отнести малое привлечение физических примеров при рассмотрении темы. Несомненным плюсом является краткость изложения материала.

А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Геометрия 7-11

Тема «Векторы и координаты» изучается в начале 9 класса. Определению  вектора предшествует разбор понятий векторных и скалярных величин. Вектор определен, как направленный отрезок. Вводится определение сонаправленных векторов, коллинеарных и ортогональных векторов, доказывается признак сонаправленности. Следует отметить, то, что работа над векторами не ограничена плоскостью, отдельные пункты доказательств даются для векторов в пространстве. Кроме этого отличительным признаком изложения темы в данном учебном курсе является то, что авторы уделили должное внимание раскрытию взаимосвязи понятий равенства и эквивалентности векторов как множеств отрезков имеющих одинаковую длину и направление. В §2 дается определение суммы векторов, которое иллюстрируется правилом треугольника на примере перемещения физического тела из точки в точку. Также на примере действия двух векторов скорости вводится правило параллелограмма. В пункте 2.3 определяется вычитание векторов, как операция, обратная сложению. Понятие противоположного вектора возникает, при необходимости свести разность к сложению. В §3 вводится правило умножения вектора на число, на основе которого доказываются основные свойства умножения и теорема о свойстве коллинеарных векторов.

Вывод: Как и в предыдущих учебниках, вектор изучается, как направленный отрезок. Материал  темы строго не разделен плоскостью и пространством, и содержит различный дополнительный материал, позволяющий раскрыть тему. Такой углубленный подход обусловлен тем, что учебник изначально предназначен для учащихся школ и классов с физико-математическим профилем. К недостаткам изложения можно отнести относительно малый объем визуальной информации по теме, в которой он так необходим. Но это характерная особенность изложения не только одного отдельно взятого вопроса. Наглядную картину о количестве визуальной информации дает, например, диаграмма [10]

Таблица 3.Визуальная информация в учебных пособиях

 

1.4. Изучение векторного метода в средней школе.

 

Цели изучения векторного метода в средней школе:

1) дать эффективный метод решения различных геометрических задач (как аффинных, так и метрических) и доказательства теорем;

2) показать широкое применение векторного аппарата в других областях знаний: технике, физике, химии, лингвистике и т. д. и на базе этого формировать учащихся диалектико-материалистичное мировоззрение;

3) использовать векторный метод при решении задач с целью формирования у учащихся умения выполнять обобщение и конкретизацию;

4) формировать у учащихся такие качества мышления, как: гибкость (не шаблонность), целенаправленность, рациональность, критичность и др.

 

Основные компоненты векторного метода решения задач:

Рассмотрим решение следующей задачи векторным методом.

«В треугольной пирамиде DABC плоские углы при вершине равны по 90°. Боковые ребра AD=6, DB=8, DC=24. Точка М равноудалена от всех вершин пирамиды. Найти расстояние DM».

Рис. 1.3. Иллюстрация к задаче

Решение:

Выберем направление осей прямоугольной системы координат так, как показано на рис. 1.3, поместив в её начало вершину D. Пусть M( x, y, z ).

Выберем базисные векторы .

Тогда разложение векторов по базисным запишется так:

Запишем условие равноудаленности точки M от вершины на векторном языке или

Выполним преобразования:

DM =13, Ответ: DM =13

Анализируя решение этой задачи, можно выделить основные компоненты векторного метода решения задач.

1. перевод условия задачи на язык векторов.
2. составление системы векторных уравнений (или одного уравнения);
3. упрощение векторных уравнений;
4. замена векторных уравнений алгебраическими и их решение;
5. объяснение геометрического смысла полученного решения этой системы (или одного уравнения).

 

Понятийный аппарат, которым должен овладеть ученик, чтобы научиться решать задачи векторным методом.

Для успешного использования векторного метода решения задач, ученик должен усвоить следующие основные понятия: вектор, начало вектора, конец вектора, одинаково направленные векторы, противоположно направленные векторы, абсолютная величина вектора (модуль вектора), равные векторы, нулевой вектор, проекция вектора на ось, координаты вектора, коллинеарные векторы, неколлинеарные векторы, единичный вектор, координатные векторы (орты), скалярное произведение векторов, угол между ненулевыми векторами.

Кроме того, он должен овладеть основными действиями, умение выполнять которые должно быть сформировано у учащихся: сложение векторов (пользуясь «правилом треугольника», «правилом параллелепипеда»); вычитание векторов, умножение вектора на число; представление вектора в виде суммы, разности двух векторов, в виде произведения векторов, в виде произведения вектора на число; заменять вектор ему равным, используя параллельный перенос; представлять вектор в виде его разложения по двум неколлинеарным векторам; переходить от соотношения между векторами к соотношению между их длинами и выполнять обратное действие; выражать длины вектора через скалярный квадрат; выражать величину угла между векторами.

Но и этого недостаточно, т. к. кроме перечисленных понятий и навыков учащийся должен овладеть компонентами метода: переводить геометрические термины на язык векторов и решать обратную задачу; переводить условие задачи на язык векторов, т. е. составлять систему векторных уравнений по условию задачи; выбирать базисные векторы, разлагать все введенные в рассмотрение векторы по базисным векторам; упрощать систему векторных уравнений; векторные уравнения заменять алгебраическими.

 

Основные этапы формирования векторного метода у учащихся.

Формирование векторного метода у учащихся можно разбить на следующие этапы:

а) подготовительный этап – его цель: овладение перечисленными основными понятиями и основными действиями;

б) мотивационный этап – его задача: показать необходимость овладения этим методом и добиться осознания того факты, что на следующих этапах целью их деятельности будет именно усвоение этого метода решения задач. Пример, используемый для этого – решение таких задач, которые векторным методом решаются проще, чем любым другим или другим вообще решить невозможно;

На мотивационном этапе можно рассмотреть с учащимися решение задачи «В трапеции ABCD углы A и B и равны по 90°, а стороны AB= 2, DC= 1, AD= 4. Докажите, что диагонали этой трапеции взаимно перпендикулярны».

Задача решается разными способами и показывается, что векторный метод решения задачи более прост.

Решение задачи векторным методом (рис. 1.4).

Что и требовалось доказать.

 

в) ориентировочный этап – разъясняется суть метода и выделяются его основные компоненты на примере анализа решенной этим методом задачи;

Рис. 1.4. Решение задачи векторным методом

 

Ориентировочный этап на основе решения данной задачи состоит в следующем:

1. Выясняется, что нужно доказать на геометрическом языке (языке, на котором сформулирована задача)?

(диагонали взаимно перпендикулярные):

— Что для этого достаточно доказать на векторном языке? (Скалярное произведение векторов и равно 0).

— Какую операцию осуществили? (Перевели требование задачи с геометрического языка на векторный).

1. Есть ли в условии задачи векторы и (Нет).

Каким образом можно получить векторы и   ?

(Ввести в рассмотрение систему координат, и записать векторы и в координатной форме).

1. Записать скалярное произведение векторов.
2. Выполнить преобразование и получается, что
3. Переводится векторное уравнение на геометрический язык.

Показывается, как можно формировать выделенные компоненты векторного метода.

Первое действие, которому необходимо научить учащихся – это перевод геометрических соотношений на векторный язык. Для формирования умения выполнять это действие целесообразно с учащимися решать задачи типа:

1. Точка принадлежит отрезку. Запишите это соотношение в векторной форме

.

1. Прочитайте запись на геометрическом языке

(Точка Mпринадлежит прямой).

1. Отрезки AB и MK параллельны. Запишите это соотношение в векторной форме.
2. Прямые AC и MP параллельны. Как записать это соотношение в векторной форме? Есть ли разница в записи решений задач 3 и 4? Почему?
3. Запишите в векторной форме условия перпендикулярности прямыхAB и PK.

Решение этих и других подобных задач желательно оформить в виде таблицы в кабинете и первое время ею пользоваться при решении задач векторным методом.

г) овладение компонентами метода – используются специально подобранные задачи для формирования отдельных компонентов метода (сначала задачи на формирование одного компонента, потом – двух, трех и т. д.);

д) формирования метода «в целом» — решаются задачи, в которых «работают» все или большинство компонентов метода, в том числе и на материале физики, химии и др. предметов.

Деление формирования метода на этапы здесь условно, так как они тесно взаимосвязаны. Очевидно, не стоит разделять ученикам четко задачи на формирование компонентов, но сам учитель должен четко знать, какой компонент с помощью какой из задач он будет формировать у учащихся. Однако цель каждого этапа должна быть ясна и учителю, и учащимся.

Выводы по 1 главе.

Формирование векторного исчисления началось с работ математиков Древней Греции, синтезирующих алгебраические и геометрические методы решения задач. Уже в то время была очевидна предметная связь со многими разделами физики и астрономии. Дальнейшее развитие понятия вектора получило в трудах Г. Весселя, и связано с его геодезическими изысканиями и геометрической интерпретацией комплексных чисел. Связь развития «многомерных» чисел и моделей, которые бы отражали их структуру дало мощное развитие векторного исчисления в работах Гамильтона, Тета, Максвелла и Грассмана, которые окончательно сформировали данный раздел в естествознании в конце 19 века.

Анализ теоретических подходов выявил достаточно большое разнообразие в определениях понятия вектора. Это закономерно, так как понятие вектора исторически формировалось в различных областях естествознания. Для реализации тех или иных целей может быть взяты за основу самые различные определения векторного пространства. Фундаментальным определением вектора было и остается его аксиоматическое определение, получившее развитие в работах Вейля. Однако такое введение понятия вектора в школьном курсе сопряжено со значительными трудностями восприятия и недостатком времени. Анализ наиболее распространённых учебных пособий по геометрии, таких как учебные пособия под ред. Л.С. Атанасяна, А.В. Погорелова, А.Д. Александрова,  выявил универсальный подход к введению понятия вектора, состоящий в замене математически строгого определения вектора его моделью, которая представляет собой направленный отрезок. Исключением является попытка ряда авторов, определить вектор, как параллельный перенос, который необходимо определять в пространстве. Несмотря на математическую строгость, она не получила достаточно широкого применения в построении курса геометрии отчасти из-за сложности работы с понятием движения в пространстве и проигрыше в наглядности, по сравнению с моделью множества направленных отрезков. Анализ решений задачи векторным методом позволяет выделить в работе основные компоненты векторного метода решения задач. Он состоит в переводе условия задач на язык векторов, составление векторных уравнений и их упрощение, перевод векторных уравнений в алгебраические, их решение и интерпретация смысла полученного решения.

---

1 2 3