ТЕСТОВЫЕ ЗАДАЧИ И УПРАЖНЕНИЯ КАК СРЕДСТВО ПОВТОРЕНИЯ ТЕМЫ ВЕКТОРЫ Часть 2

1 2 3

---

 

ГЛАВА 2. ВЕКТОРНЫЙ МЕТОД В РЕШЕНИИ ЗАДАЧ И ДОКАЗАТЕЛЬСТВА УТВЕРЖДЕНИЙ.

2.1. Основные типы задач, решаемые векторным методом.

Векторы целесообразно применять при решении двух основных типов геометрических задач: аффинных и метрических.

Задачу называют аффинной, если она не связана с измерением отрезков и углов  (прямо или косвенно). В противном случае, задачу называют метрической или евклидовой. Среди них имеются задачи на доказательство и на вычисление, планиметрические и стереометрические.

В задачах с аффинным содержанием обычно требуется установить принадлежность трёх точек одной прямой или четырёх точек одной плоскости, вычислить отношение, в котором точка, принадлежащая отрезку, делит этот отрезок, доказать параллельность отрезков или прямых, сонаправленность или противоположную направленность лучей, параллельность прямых и плоскостей. Реже встречаются задачи на нахождение различных множеств точек. В метрических же задачах преимущественно приходится вычислять расстояния и углы (междупрямыми, прямой и плоскостью, двугранные углы), доказывать перпендикулярность прямых и плоскостей и значительно реже находить и изучать множества точек на плоскости и в пространстве.

Для решения аффинных задач планиметрии, касающихся взаимного расположения двух прямых, принадлежности трёх точек одной прямой, вычисления отношения коллинеарных отрезков, удобно пользоваться векторами. В процессе решения таких задач необходимо владеть лишь операциями сложения и вычитания векторов, умножения вектора на число, которые известны из школьного курса.

Если же задача носит метрический характер, то этих операций недостаточно. На помощь приходит обычно операция скалярного умножения векторов. Посредством этой операции (в сочетании с аффинными операциями) можно вычислять расстояния и углы, находить метрические соотношения между линейными и угловыми элементами многоугольников, описывать различные множества точек, решать ряд задач, связанных с окружностью.

Рассмотрим примеры решения геометрических задач векторным методом.

Задача 1. Доказать, что средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

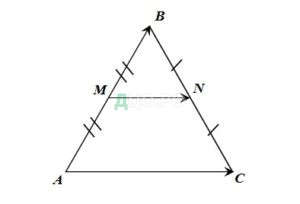
Решение.

Пусть MN – средняя линия ABC. Докажем, что  и . По “правилу треугольника”   Так как M и N– середины сторон  AB и BC, то , поэтому . Итак, .

Из этого векторного равенства следует:

а) векторы и коллинеарны, значит отрезки ACиMNпараллельны;

в) или  .

Задача 2. Дан параллелограмм и произвольная точка O пространства. Доказать, что сумма, доказать обратное утверждение, если для некоторого пространственного четырехугольника ABCD и некоторой точки O имеет место данное соотношение , то ABCD – параллелограмм

Задача 3. В плоскости треугольника ABC найти такую точку O, что .

Решение.

точка O – точка пересечения медиан DABC, т.е. точка O– центр тяжести DABC.

Задача 4. Даны два отрезка AB и CD. Доказать, что если , то. Верно ли обратное утверждение?

Решение.

Рассмотрим векторы и . В зависимости от их взаимного расположения может получиться плоская или пространственная фигура.

Учитывая, что , преобразуем данное равенство следующим образом:

а это и означает, что .

Выполняя преобразования “от конца к началу”

( или , или и т.д.), убеждаемся в том, что верно и обратное утверждение.

Задача 5. В равнобедренном треугольнике медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найти угол между боковыми сторонами этого треугольника.

Решение

Пусть  в треугольнике . Медианы BB1и по условию перпендикулярны, поэтому

Разложим векторы и по векторам и .

Имеем:

Из равенства (1) следует:

Обозначив и , воспользуемся определением скалярного произведения.

Тогда получим: отсюда

Задача 6. Доказать, что при произвольном выборе точки O равенство (1) является необходимым и достаточным условием принадлежности различных точек         A, B, C одной прямой.

Решение.

Достаточность. Пусть выполняется равенство (1).

Из него находим, что , отсюда по формуле вычитания векторов .

Следовательно, векторы и коллинеарны, а точки A, B, Cпринадлежат одной прямой.

Необходимость. Если точки A, B, C принадлежат прямой, то и коллинеарны, поэтому . Применим формулу вычитания векторов:

, или .

 

Задача 7. В параллелограмме OABC точки M и  N— середины сторон OC и CB.

Найти отношение:

где

Решение.

Пусть и . По условию задачи

. Для точек P, M, Aприменим условие принадлежности трёх точек одной прямой         (см. предыдущую задачу). Тогда получим:

Следовательно,

, или

Пользуясь однозначностью разложения вектора по двум неколлинеарным векторам, можно записать:

и . Отсюда .

Задача 8. Доказать, что плоскость, проходящая через концы трёх рёбер куба, имеющих общую точку, перпендикулярна диагонали куба, выходящей из этой точки.

Решение. Рассмотрим в кубе ABCDA1B1C1D1        диагональ A1C и сечение AB1D1.

Требуется доказать, что (A1C)^(AB1D1).Для этого достаточно установить, что (A1C)^(AB1), (A1C)^(AD1). Разложим векторы и по векторам

Тогда

Так как и , то , поэтому

Отсюда: (A1C)^(AB1). Аналогично доказывается, что (A1C)^(AD1). Следовательно, (A1C)^(AB1D1).

Задача 9. Доказать, что если в тетраэдре две пары противоположных рёбер взаимно перпендикулярны, то и  третья пара рёбер также взаимно перпендикулярна.

Доказательство. Пусть OABC – данный тетраэдр, у которого OA^CB и OB^AC.

Требуется доказать, что OC^AB. Для решения задачи введём в рассмотрение векторы , и и запишем данные условия, используя скалярное произведение векторов. Так как OA^CB, то или . Так как OB^AC, то или . Сложив эти два соотношения, получаем , , т.е. . Отсюда седует, что прямые OC и ABвзаимно перпендикулярны.

Задача 10.(Теорема косинусов) Доказать, что для любого треугольника ABC имеет место соотношение:

Решение. Введём обозначения: , , . Очевидно, . Отсюда , или .

Используя геометрический смысл скалярного произведения (Скалярное произведение векторов равно произведению модулей данных векторов на косинус угла, образованного данными векторами.), получаем искомый результат.

Следствием этой задачи являются прямая и обратная теорема Пифагора: для того чтобы треугольник ABC был прямоугольным с прямым углом при вершине A, необходимо и достаточно, чтобы  .

Скалярное произведение векторов равно произведению модулей данных векторов на косинус угла, образованного данными векторами.

Задача 11. В треугольнике ABC вычислить длину медианы ma, зная угол A и две стороны AB=c, AC=b.

Решение. Пусть M– середина стороны BC треугольника ABC. Согласно теореме “Основные свойства скалярного произведения векторов”.

Для произвольных векторов , , и любого числа имеем:

д) имеем: . Согласно лемме: “Если ABC – произвольный треугольник, а M – середина стороны”BC, то . Имеем: , где и . Подставив это значение в предыдущее соотношение, получаем:

Задача 12. Доказать, что высоты любого треугольника имеют одну общую точку.

Решение. Пусть ABC – данный треугольник, O – точка пересечения двух высот и .

Если обозначить через , и соответственно векторы , и , то

и , поэтому и .

Воспользуемся следующим тождеством, в справедливости которого легко убедиться, если раскрыть скобки:

 

Учитывая предыдущие соотношения, получаем:

или  . Отсюда следует, что — высота треугольника ABC.

2.2. Доказательство алгебраических и геометрических неравенств, с применением скалярного произведения.

 

При решении и исследовании многих задач арифметики, алгебры, анализа и геометрии приходится непосредственно или косвенно рассматривать неравенства и системы неравенств, применять свойства неравенств. Помимо известных приёмов решения задач на неравенства, в основе которых лежит теорема Коши, можно предложить дополнительно ещё неравенства, связанные со скалярным произведением:

Причём в (2) знак равенства имеет место тогда и только тогда, когда векторы и линейно зависимы (т.е. коллинеарны).

Более подробно: если , то ;  если , то  . Эти два неравенства позволяют доказать известные неравенства и открывают путь для получения новых неравенств, не рассматривавшихся в школьной учебной литературе.

Ниже будут приведены решения геометрических и алгебраических задач на неравенства посредством формул (1) и (2).

 

Задача 1. Доказать, что для каждого треугольника ABC выполняется неравенство , где R – радиус описанной окружности, r – радиус вписанной окружности. 

Решение. Пусть O – центр описанной окружности, I – центр вписанной окружности. Тогда, как известно,

Следовательно, , причём знак равенства имеет место только для равностороннего треугольника. Далее имеем:

Но поэтому    .

После упрощений получаем:

Сократив на  и положив .

Найдём: или .

Задача 2. Найти наибольшее и наименьшее значения функций 

Решение.  Рассмотри два вектора:

Согласно неравенству (2)

, где

Имеем

задача 3. Даны четыре точки A, B, C и D. Доказать, что

Решение. Пусть M – середина отрезка AB, N – середина отрезка CD.

Тогда

Отсюда причём знак равенства имеет место только тогда, когда M=N, т.е. когда ABCD – параллелограмм.

Имеем:

2.3.  Тестовые задания по переводу геометрического содержания задачи на векторный язык

Практика показывает, что в процессе решения задачи векторным методом самым трудным для учащихся является умение делать перевод геометрического факта на язык векторов и осуществлять обратный переход.

Для овладения учащимися векторным методом решения геометрических задач важно научиться делать перевод геометрического факта на язык векторов и обратный перевод, т.е. получение геометрической интерпретации векторного выражения.

Чтобы сформировать у учеников умение переводить текст задачи на векторный язык, следует отработать сначала перевод отдельных элементов текста задачи и их связей на векторный язык, а уж затем чтение векторных соотношений. Для выработки отмеченных навыков целесообразно использовать тестовые задания, позволяющие переводить основные геометрические понятия на язык векторов и находить геометрические интерпретации векторных выражений. Создание такого тестового «словаря» систематизирует знания учеников по векторной алгебре, помогает правильно выбрать векторы, которые удобно использовать для решения задачи, а также помогает записать условие задачи с помощью выбранных векторов и сделать соответствующие выводы и обобщения по мере выявления зависимости между ними. Составление перечня заданий в таком тестовом «словаре» целесообразно начинать с первых уроков знакомства учащихся с векторами. По мере изучения теории и в процессе решения задач появляются новые векторные соотношения, которые постепенно включаются в «словарь». Формулы перевода основных геометрических соотношений на векторный язык удобно оформлять для общего пользования учащимися в виде таблиц, и употреблять при тестировании как можно чаще.

Следует помнить, что:

аффинные свойства фигур могут быть выражены на языке векторов посредством линейных операций над векторами, а в некоторых случаях и с помощью скалярного произведения. Например, если векторы и сонаправлены, то  , где . С другой стороны, можно воспользоваться и скалярным произведением:   или . Аналогично,  если ABCD – параллелограмм, то или . В случае же, когда свойство фигуры  метрическое, оно выражается непременно через скалярное произведение; одних аффинных понятий для выражения этих свойств недостаточно. Поэтому в приводимом ниже тестовом «словаре» имеются три раздела:

а) аффинные свойства, записанные на языке линейных операций (1-11);        б) метрические свойства (12-20*, 24*-28*); в) аффинные свойства, выраженные на языке скалярного произведения с привлечением линейных операций (21-23*).

*Звёздочкой отмечены дополнения к основным записям, реже применяемые и предназначенные для работы с наиболее успевающими учениками.

1. а) Для любых трёх точек A, B, C имеем .                                                                 

    б) Для любых точек A, B и произвольной точки O имеем: .

2. а) Если M – середина отрезка AB,  то для любой точки O справедливо равенство: 

. 

   б) Если равенство справедливо для какой-либо точки O, то M – середина отрезка AB.

2.* Если M и N – середины отрезков AB и CD, то справедливы равенства и .

 

3. Точки M и M1 тогда и только тогда симметричны относительно точки O, когда .

3.* Если точки M и M1 симметричны относительно середины отрезка AB, то

4. Точка C делит отрезок AB в отношении тогда и только тогда, когда .
5. Четырёхугольник ABCD в том и только в том случае будет параллелограммом, если выполнено одно (любое) из следующих условий:

а) ;                        б) ;

в) (O – произвольная точка).

6. Точка G в том и только в том случае является точкой пересечения медиан треугольника ABC, если:

а) ;

б) ,

где O – произвольная точка. 

7. Прямые AB и CD параллельны тогда и только тогда, когда , где .
8. Точка M принадлежит прямойOA тогда и только тогда, когда  .

8.* Если — направляющий вектор прямой и , то:

а) для любой точки  и любой точки O (не обязательно принадлежащей прямой ) имеет место равенство ;

б) для любой точки справедливо равенство ; при этом число k однозначно определяется точкой P.

9. Множество точек C, для которых (где ), есть отрезок ABпри, луч BA при , луч AB при .

9.* 1) Если — полуплоскость с границей (AB) и O – любая точка этой полуплоскости, не принадлежащая (AB), то

     2) Если — полоса, определяемая парой параллельных прямых AB и CD, то

.

10. Если и —  неколлинеарные векторы, параллельные плоскости , то для любой точки имеем , где k, l – числа, однозначно определяемые точкой P. Обратно, если выполнено равенство , то .

10.* Если точки A, B, C не лежат на одной прямой, то точка D тогда и только тогда принадлежит плоскости ABC, когда

(точка O – произвольная). 

11. Если , где -гомотетия с центром  A и коэффициентом k, то.

11.* 1) Если , , то .

2) Если , то, где O — произвольная точка.

3) Композиция двух гомотетий и при есть гомотетия , где точка C определяется равенством (для любой точки O). Если , то точка C делит отрезок AB в отношении , которое зависит только от  коэффициентов гомотетий, но не зависит от центров гомотетий.

12. Если , то

а) ;

б)* , где O — любая точка.

13. Если , то

а) ;

б)* , где O — произвольная точка.

14. Для любых двух векторов и имеем.
15. Треугольник ABC — прямоугольный (), если

а) ;

б)* .

16. Треугольник ABC -равнобедренный, если выполнено какое-либо из следующих условий:

а) ;

б)* ;

в)* .

17. Треугольник ABC -остроугольный, если одновременно выполняются неравенства и.
18. Треугольник ABC — тупоугольный, если либо ,  либо , либо .
19. Для любых трех точек A, B, C имеем:

.

19.* Для любых четырёх точек A, B, C, D имеем:

.

20. Если — единичный вектор, то есть проекция вектора на ось с направляющим вектором .

20.* Если — направляющий единичный вектор прямой p, то составляющая вектора на прямой p вычисляется по формуле .

21. Векторы и коллинеарны тогда и только тогда, когда выполнено одно (любое) из следующих условий:

а) ;

б)* ;

в)* .

22. Четырёхугольник ABCD — трапеция тогда и только тогда, когда .

22.* 1) Четырёхугольник ABCD — прямоугольник тогда и только тогда, когда для любой точки M выполняется

2) Четырёхугольник ABCD — параллелограмм тогда и только тогда, когда

.точка M — середина отрезка AB тогда и только тогда, когда

(O — произвольная точка).

23.*  Точка G — точка пересечения медиан треугольника ABC тогда и только тогда, когда выполняется одно (любое ) из следующих условий:

 

24.* Точка H тогда и только тогда является точкой пересечения высот треугольника ABC, когда выполнено одно (любое ) из следующих условий:

а) , где O — центр описанной окружности около треугольника ABC;

 

25.*Если O– центр описанной около треугольника окружности, то

 

26.*Если I – центр вписанной в треугольник окружности, то выполняется одно (любое) из

27. Треугольник ABC – равносторонний тогда и только тогда, когда, гдеO– центр описанной (вписанной) окружности.
28. Если H – точка пересечения высот ортоцентрического тетраэдра ABCD, то , гдеO– центр описаннойсферы. (Тетраэдр называется ортоцентрическим, если его высоты пересекаются в одной точке).

Опыт показывает, что учащиеся лучше переводят геометрические факты на язык векторов, чем дают геометрическую интерпретацию полученной векторной записи, поэтому в процессе работы следует обращать внимание учащихся на то, что запись одного и того же геометрического факта неоднозначна.

Приведём две задачи на выработку навыка геометрической интерпретации векторных соотношений.

Задача 1. Дать геометрическую интерпретацию векторных выражений:

Решение. Рассмотрим параллелограмм ABCD, для которого , . Имеем , . При этих обозначениях можно дать следующую интерпретацию записанных равенств.

а) Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

б) Разность квадратов диагоналей параллелограмма равна учетверенному произведению его смежных сторон на косинус угла между ними.

в) Рассматриваемое векторное соотношение можно записать в виде

Отложим векторы ,, от некоторой точки O, т.е. , , , и рассмотрим треугольник ABC. Видим, что , где G — точка пересечения медиан треугольника ABC. Так как ,, , то рассматриваемому равенству можно дать следующую геометрическую интерпретацию: квадрат расстояния любой точки пространства до точки пересечения медиан треугольника равен одной третьей суммы квадратов расстояний этой точки до вершин треугольника без одной девятой суммы квадратов длин сторон треугольника. Если взять тетраэдр OABC, у которого ,, , то , где G – центроид треугольника ABC, и мы получаем такую интерпретацию: квадрат медианы OG тетраэдра равен одной третьей суммы квадратов ребер тетраэдра, сходящихся к вершине O, без одной девятой суммы квадратов длин сторон противолежащей грани.

г) Чтобы дать геометрическую интерпретацию этого векторного выражения, рассмотрим тетраэдр ABCD. Обозначим ,, , , тогда ,,, ,, .

Отсюда:

где P, Q – середины отрезков AC, BDсоответственно. Векторное тождество показывает, что учетверённый квадрат расстояния между серединами двух противоположных ребер тетраэдра равен сумме квадратов длин остальных рёбер без суммы квадратов длин рассматриваемых противоположных рёбер.

Аналогично можно сформулировать эту теорему применительно к четырёхугольнику: учетверённый квадрат отрезка, соединяющего середины диагоналей четырёхугольника, равен сумме квадратов всех его сторон без суммы квадратов его диагоналей.

д) Рассмотрим параллелепипед, построенный на векторах ,,, тогда имеем: квадрат длины диагонали параллелепипеда равен сумме квадратов длин диагоналей его граней OAB, OBC, OCA без суммы квадратов ребер, исходящих из вершины O. Это векторное равенство можно также получить и путём упрощения равенства в), а их геометрические интерпретации, как видим, различны.

Задача. Определить вид треугольника ABС,для которого выполняется условие , где G– точка пересечения медиан треугольника.

Решение. Из равенства следует,  что . Тогда ,

Но векторы и неколлинеарны, следовательно,

Из полученной системы находим, что

Итак, данное равенство выполняется только для равностороннего треугольника.

Проанализировав ход решения задач 1 и 2, отметим, что важен не просто поэлементный перевод условия задачи на язык векторов; в зависимости от ситуации, от содержания задачи одни и те же слова переводятся на векторный язык разными средствами. Задачи на выработку геометрической интерпретации векторных выражений способствуют более глубокому пониманию изучаемого материала, активизируют деятельность учащихся по применению полученных знаний.

Приведём пример решения задачи с помощью изложенного «словаря».

Задача. Если точка A пересечения диагоналей четырехугольника MNPQи средины B,C его противоположных сторон MNиPQ лежат на одной прямой, то MNPQ – трапеция или параллелограммы

Решение: положим ,. Тогда и . Так как B — середина отрезка MN, то:

Аналогично,

По условию точки A, B, C лежат на одной прямой, и поэтому, существует такое число m, что:

или .

Откуда следует, что m = k = l.

Тогда: ,,

т.е. (7). Следовательно, , т.е. MNPQ — трапеция или параллелограмм.

Выводы по второй главе.

Самое трудное для учащихся – это научиться делать перевод геометрического факта на язык векторов и обратный перевод. Для овладения учащимися векторным методом решения геометрических задач важно научиться делать перевод геометрического факта на язык векторов и обратный перевод, т.е. получение геометрической интерпретации векторного выражения.

---

1 2 3