Вопросы преподавания теории вероятностей в cтарших классах

1  2

---

ОГЛАВЛЕНИЕ

 

Глава 1 Теоретические основы изучения элементов теории вероятностей в старшей школе

1.1 Психолого-педагогические основы изучения в старших классах тематического модуля «Элементы теории вероятностей»

1.1.1 Психолого-педагогические особенности учащихся старших классов

1.1.2 Технология модульного обучения

1.2 Методические основы обучения учащихся старших классов принципам решения задач

Глава 2 Изучение современного состояния проблемы обучения учащихся старших в теме «Элементы теории вероятностей»

2.1 Базовые понятия и законы теории вероятности и особенности их представления учащимся общеобразовательной школы

2.2 Анализ нормативных документов

2.3 Анализ изложения элементов теории вероятностей в учебниках и программах

Глава 3 Методические аспекты преподавания в старших классах темы «Элементы теории вероятностей

3.1 Методологическая база исследования

3.2. Проведение констатирующего эксперимента

3.3 Разработка и внедрение модульной программы.

3.4 Анализ результатов опытно-экспериментальной работы

Заключение

Библиографический список

Приложения

 

ВВЕДЕНИЕ

 

Задача современной школы – сформировать гармонично развитую, компетентную личность, способную эффективно осуществлять жизнедеятельность в окружающем мире и социуме. С этой целью у школьника необходимо сформировать, в первую очередь, умение учиться, способность распознавать и применять определенные правила действий в той или иной ситуации.

Специфика школьного курса математики заключается в том, что данный предмет направлен на формирование основ мыслительной деятельности школьников, развитие логического мышления, умения систематизировать, проводить быстрые расчеты, применять алгоритмы и формулы и проч. Данные знания и умения пригодятся абсолютно каждому человеку в процессе обычной жизни [27].

Для того, чтобы суметь правильно сориентироваться в жизненной ситуации, применить определенные знания, найти решение, попытаться из нескольких вариантов решений выбрать более целесообразное – необходимы достаточно развитые творческие способности, быстрота и гибкость мыслительных процессов.

В то же время, школьные программы, учебники и задачники зачастую содержат достаточно мало заданий, развивающих данные способности. Программный материал больше нацелен на решение сугубо математических выражений, уравнений, задач на применение математических формул и т.п. К тому же, исследования уровня развития логического мышления у подростков показали, что логическое мышление у большинства школьников находится на недостаточном уровне развития [4; 16; 34].

На сегодняшний день возникла необходимость выбора наиболее эффективных методов и технологий, обеспечивающих доступ школьников к качественному образованию в соответствии с их индивидуальными способностями, склонностями и потребностями. Реализация концепции модернизации образования требует развития системы специализированной подготовки учащихся, с учетом индивидуализации обучения, расширения и углубления методов обучения с учетом инноваций.

Стоит отметить, что современные учителя ведут активный поиск способов развития логических способностей учащихся на уроках математики. Формирования умений самостоятельно ориентироваться в постоянно растущем объеме информации, применять имеющиеся знания с максимальной пользой, создавать наиболее выгодные условия для приобретения новых знаний и для сообщения их другим. Перечисленные умения играют большую роль не только в процессе обучения, но и во всей жизнедеятельности человека.

Следовательно, актуальной является проблема поиска эффективных подходов, способствующих развитию логического мышления на уроках математики.

Одним из аспектов формирования логики и нестандартного подхода к решению задач выступает тематический блок «Элементы теории вероятностей», изучаемый в курсе математики старшей школы.

На сегодняшний день значительная часть естественнонаучных и социально-экономических знаний базируется на знании вероятностных законов. В то же время, без соответствующей специальной подготовки невозможно адекватное восприятие и интерпретация подобной информации. Обострившиеся социальные, политические, экономические и даже бытовые проблемы требуют от человека умения анализировать случайные факторы и события, принимать решения в ситуациях, имеющих вероятностную основу. Вопросам использования элементов теории вероятностей в школьном курсе математики посвящены работы И.В. Белько, В.А. Булычева, Е.А. Бунимовича, И.Р. Высоцкого, Е.С. Вентцель, В.Е.  Гмурмана, М.А. Матальского, Ю.Н. Тюрина, В.В. Фирсова и др.[3; 5; 6; 8; 11; 20; 31; 33]

Однако, на сегодняшний день процедура проектирования программы, отвечающей современным запросам законодательства и действительности, обеспечивающей многоуровневое разностороннее применение математического аппарата, рассмотрена недостаточно. Необходима планомерная разработка методических приемов включения блока теории вероятности в программный материал математического образования старшей школы.

Проблема исследования состоит в необходимости совершенствования методики преподавания Теории вероятностей в курсе математики старших классов общеобразовательной школы.

Объект исследования: программа математики старшей школы.

Предмет исследования: изучение возможности оптимизации общего интеллектуального, математического и личностного развития старшеклассников посредством тематического блока «Элементы теории вероятности».

Цель исследования: изучить особенности преподавания Теории вероятностей в школьном курсе математики и разработать методические рекомендации, позволяющие формировать ключевые и предметные компетенции учащихся посредством данного тематического блока.

Гипотеза исследования: проектирование новой методики преподавания Теории вероятности на старшей ступени общего образования будет способствовать успешному развитию общих и предметных компетенций учащихся при соблюдении следующих условий:

1. Учет возрастных и индивидуальных особенностей обучения старшеклассников элементам теории вероятностей,
2. Разработка подходов к обеспечению дифференцированного содержания обучения для предоставления возможности реализации каждым учащимся собственных способностей в усвоении материала.

Для реализации цели и проверки гипотезы нами были поставлены задачи:

1. Раскрыть структуру математического образования в старшей школе.
2. Определить роль теории вероятностей в развитии логического и творческого мышления школьников – как условия их успешной социализации и самореализации в обществе.
3. Определить основные методические особенности преподавания «Теории вероятностей», позволяющие развивать ключевые и предметные компетенции школьников.
4. Разработать структурно-функциональную модель проектирования тематического блока «Теория вероятности» в курсе старшей школы.
5. Разработать методику решения задач по теории вероятностей на ЕГЭ и ОГ

Теоретико – методологическую основу исследования составили:

• компетентностный подход в образовании (И.А. Зимняя, В.В. Сериков, А.В. Хуторской);
• теории прикладной и практической направленности математического образования, (Р.М. Асланов, Б.В. Гнеденко, Г.Л. Луканкин, А.Г. Мордкович, , А.А. Русаков, В.В. Фирсов, и др.);
• труды, посвященные проектированию методики преподавания отдельных тем в курсе старшей школы (Н.Я. Виленкин, В.С. Лютикас, В.В.Орлов, Т.В. Черникова и др.).

Методами исследования стали:

— теоретический анализ и систематизация данных педагогической, математической литературы по теме исследования,

— анализ содержания учебных программ и практики преподавания теории вероятностей в старшей школе;

— теоретическое моделирование;

— разработка системы уроков по формированию навыков использования теории вероятности при решении задач.

Актуальность исследования заключается в том, что определены методические особенности преподавания теории вероятностей в современной школе и разработана схема проектирования тематического блока с целью реализации методических особенностей преподавания математики в старших классах.

Теоретическая значимость исследования обусловлена предоставлением систематизированной и структурированной информации по проектированию тематического блока «Элементы теории вероятностей», которая позволяет по- новому строить целевой, содержательный и процессуальный компоненты преподавания математики.

Практическая значимость исследования состоит в:

• разработке модели и программы преподавания теории вероятности, направленных на развитие ключевых компетенций учащихся,
• создании методического обеспечения преподавания блока «Элементы теории вероятностей».

Материалы данного исследования могут быть использованы учителями математики и репититорами в профессионально-педагогической деятельности.

Глава 1 Теоретические основы изучения элементов теории вероятностей в старшей школе

 

1.1 Психолого-педагогические основы изучения в старших классах тематического модуля «Элементы теории вероятностей»

1.1.1 Психолого-педагогические особенности учащихся старших классов

 

Особенности мышления являются основой для общего развития личности старшеклассников. На формирования ведущего типа мышления оказывают влияние различные психологические особенности, такие как восприятие, уровень развития внимания, тип и свойства памяти.

Исследованию процессов мышления в психологии и педагогике уделяется серьезное внимание, как основе интеллектуального и общего развития личности.

Под мышлением понимают социально обусловленный, связанный с речевой сферой, психический процесс познания нового, обобщенного и опосредованного отражения действительности путем её анализа и синтеза. [34, С. 35].

Большинство авторов отмечают, что мышление — высшая форма отражения мозгом окружающего мира, наиболее сложный познавательный психический процесс, свойственный только человеку.

Другие авторы рассматривают мыслительную деятельность, как один из мощнейших факторов развития цивилизации сегодняшнего дня» [4, с. 132]. Исследователи выделяют три основных вида мышления:

1. Предметно-действенное.
2. Наглядно-образное.
3. Словесно-логическое.

Предметно-действенное мышление позволяет учащимся сформировать определенные навыки обращения с предметами, их преобразования и применения в повседневной жизни. Начальными этапами формирования подобных умений являются элементарные действия с числами, изображения и соединения отрезков в фигуру и проч. В дальнейшем такие способности развиваются в осуществление практического анализа, конструирования процессов, предметов и явлений, что является важной характеристикой профессиональных навыков в разных сферах деятельности [21, с. 124].

Следует отметить особенности развития мышления старших подростков: они способны абстрагироваться от конкретного наглядного материала, переводя образы в слова, анализируя, доказывая и формулируя гипотезы.  Ведущими в данном возрасте становятся формально-логические операции, гипотетико-дедуктивное мышление. Особенности рефлексивной деятельности позволяют анализировать идеи, искать ошибки и выявлять противоречия в суждениях. Старшеклассник способен на системный поиск решений. Сталкиваясь с новой задачей, он старается найти различные пути ее решения, проверяя эффективность каждого и выбирая наиболее целесообразный. Для данного периода характерен интерес к абстрактным философским, религиозным, политическим и прочим проблемам, уровень которого зависит от особенностей развития интеллекта. Подростки рассуждают о будущем, вырабатывают собственные теории, приобретают более глубокий и обобщенный взгляд на мир. У них появляется склонность к самоанализу, приобретаются основы самовоспитания, самоорганизации и самоконтроля. Происходит активная интеллектуализация таких психических функций, как память и восприятие, воображение и креативность.

В то же время, этому возрасту присуща развитая способность к фантазированию, выстраиванию грандиозных, часто фантастических и утопических планов. Амбиции и стремления подросткового возраста, отношение к явлениям окружающей жизни, людям и событиям отличаются определенным максимализмом. Эмоциональные реакции сильно обострены. Однако, по мнению многих исследователей, именно этот факт способствует тому, что данный возраст становится сенситивным к развитию новых, нестандартных способов мышления.

В.Г. Сухомлинский отмечал важную роль логических и нестандартных задач в развитии мышления детей и формировании всесторонне развитой личности [29]. Поскольку логические задачи представляют собой не простое задание на применение определенных формул и алгоритмов, а требуют умения анализировать, обобщать, проводить аналогии, находить общее и проч. Данные умения являются чрезвычайно важными свойствами личности, помогающими ей адаптироваться в окружающем мире.

Наглядно-образное мышление опирается на восприятие или представления. Этот вид мышления связан с ярким и живым представлением тех или иных предметов или явлений. То есть, если ученику объяснять при помощи словесного метода понятие длины и направления, он, возможно, сформирует в сознании некий абстрактный образ. Однако он будет неточным или даже ошибочным. Если же преподаватель изобразит данные линии или продемонстрирует при помощи ленты, нитки, рисунка – данные понятия приобретут конкретику. Можно долго объяснять младшим школьникам состав числа или правила сложения и вычитания, но достаточно несколько раз продемонстрировать на примере конфет, яблок, стаканов и проч. – и у них сформируется ясное понимание данных процессов и характеристик.

Логическое мышление позволяет сознанию ребенка выйти за пределы непосредственного опыта ощущения и восприятия. Оно характеризуется определенной степенью абстрактности, которая позволяет судить о тех процессах и явлениях окружающего мира, которые человек непосредственно не наблюдает [24, с 125].

З.И. Калмыкова отмечает важность продуктивного (деятельностного) мышления и таких его характеристик, как глубина, гибкость, устойчивость, самостоятельность и осознанность [13, с.37-40].

Р.С. Немов отмечает значимость научного мышления, как выражения мышления логического, обосновывая его с позиций правильности и безошибочности суждений. [25, с. 316]. Автор утверждает, что мышление для логики – это абстрактный процесс рассуждения, включающий в себя логические операции, умозаключения и выводы, которые сами по себе могут рассматриваться как правильные и неправильные независимо от того, кто эти операции, умозаключения и выводы составляет.

Н.А. Менчинская отмечает, что логическое мышление характеризуется способностью к оперированию суждениями, терминами, понятиями и умозаключениями, а его развитие сводится к развитию логических приёмов мышления [21, с. 38].

Л.М. Фридман и другие исследователи также указывают, что в основе логического мышления лежат логические операции, умозаключения и выводы. Из чего возникает необходимость подробнее рассмотреть приведенные компоненты логического мышления [34, с. 106-108].

1) Способность к сравнению, то есть, сопоставлению объектов, нахождению сходств и различий. Посредством сравнения математических категорий школьники учатся воспринимать форму предметов, их размер, определять положение в пространстве и относительно других объектов. Сравнение позволяет научиться сопоставлять количественные характеристики явлений, знакомит с сущностью понятий «больше – меньше — равно», «высокий — низкий», «близкий — далекий», «длинный — короткий» и т.п.  Подобные характеристики приводят к более глубокому проникновению в суть явлений и предметов окружающего мира.

2) Аналитическое мышление, то есть, способность разбивать изучаемый объект на составные части, выделение отдельных частей, признаков и свойств. Посредством анализа дети учатся понимать состав числа, осознают понятие целого и дробного числа, глубже понимают сущность процессов сложения – вычитания, умножения – деления. Анализ геометрических фигур позволяет выделить в сложном объекте его составляющие, что помогает развивать творческое мышление, развивает способности к черчению и рисованию, предметное отношение к окружающим предметам. Аналитические умения также помогают ребенку в любой жизненной ситуации действовать по алгоритму, применять основополагающие знания и умения в меняющихся жизненных ситуациях

3) Способность к синтезу. Данная способность является логическим продолжением и развитием аналитических способностей. Оно позволяет учащимся из отдельных частей, характеристик, свойств, частей складывать единое целое. Синтез отдельных характеристик изучаемого объекта или явления позволяет учащимся формировать в сознании более полную картину окружающего мира. С одной стороны, ребенок учится понимать состав объекта, с другой – понимает логику возможности или невозможности объединения отдельных частей, характеристик и проч.

4) Абстрактное мышление. Способность к абстрагированию от конкретных признаков и характеристик явлений и процессов позволяет воспринимать окружающий мир  во всем его многообразии, включая свойства, о которых у учащегося еще нет определенных знаний. Данное свойство психики основано на формировании в воображении отвлеченной, и в то же  время, целостной и реальной, картины изучаемого явления. Способность к абстрактному мышлению является важной ступенью к формированию и развитию творческих способностей, обогащает внутренний мир и эмоциональную сферу детей. Посредством абстракции учащиеся могут мысленно объединять процессы и предметы в группы, что лежит в основе понимания и запоминания определений, правил, способности к классификации, умению делать выводы.

5) Конкретизация. Несмотря на важность абстрактного мышления для личностного развития ребенка, способность четко представлять отдельные характеристики явления лежит в основе правильного восприятия предметов и явлений, позволяет избегать ошибок и путаницы. Способность к конкретизации позволяет выделить главное путем постепенного перехода от общего к частному. Данная способность развивается посредством углубления изучения предмета, когда уже достаточно известный объект подвергается более тщательной оценке. Так, например, понимание того, что предмет представляет собой большой квадрат, является общей, но не конкретной характеристикой объекта. Для более точного его представления уточняются численные показатели длины, высоты, ширины и т.п. — это мысленный подход от общего к единичному, которое соответствует этому общему. Конкретизация объекта связывает теоретические знания с жизнью, с практикой и помогает правильно понять действительность. Отсутствие конкретизации приводит к формализму, оторванности знаний от реальной жизни.

6) Формулировка суждений. Характеризует умение учащихся отражать или утверждать связи между отдельными предметами или явлениями окружающей действительности. Данная характеристика демонстрирует достаточно высокий уровень сформировнности логического мышления, так как является показателем самостоятельности и основательности мыслительной деятельности учащегося, наличия у него определенной системы знаний, представлений о мире, развитых речевых показателей, уверенности, наличия собственного мнения и умения его высказывать. Другими словами, умение высказывать обоснованные суждения характеризует высокий уровень развития личности.

7) Умозаключение. Заключается в способности формулировать выводы на основании анализа нескольких суждений. Умозаключение может быть продолжением, развитием существующего суждения, синтезом нескольких сходных точек зрения, или же совершенно самостоятельном мнении, основанном на анализе ошибок, допущенных в различных формулировках.

Формирование логического мышления является одной из важнейших составляющих педагогического процесса. Учитель должен помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал. Успешная реализация этой задачи во многом зависит от сформированности у учащихся познавательных интересов. В данном отношении математика даёт реальные предпосылки для развития логического мышления, а задача учителя сводится к наиболее полному и всестороннему использованию данных возможностей при обучении детей. [16, с.74-76].

При этом наибольшие возможности и перспективы для развития логического мышления предоставляет именно раздел «Теория вероятностей», поскольку решение вероятностных задач невозможно без рассуждений, умозаключений, выявления закономерностей – что и составляет основу логики.

При анализе логического мышления и его структуры О.К. Тихомиров выделяет следующие ключевые элементы:

1. Определённость условий задачи.
2. Логика проверяемых признаков и информативность поисковых фактов. [29, с. 115.]

Однако, педагогами отмечается недостаточность четко структурируемых и логически описываемых математических знаний и представлений для глубокого понимания школьниками всей сложности и многообразия процессов окружающего мира. Так, Б.В. Гнеденко писал: «Давно назрел и не терпит дальнейших отлагательств вопрос о введении в школьный курс математики элементов вероятностно-статистических знаний. Законы жёсткой детерминации, на изучение которых целиком ориентировано наше школьное образование, лишь односторонне раскрывают сущность окружающего мира. Случайный характер многих явлений действительности оказывается за пределами внимания наших школьников. В результате этого их представления о характере многих природных и общественных процессов носят однобокий характер и неадекватны современной науке. Необходимо познакомить их со статистическими законами, раскрывающими многогранные связи бытия предметов и явлений» [12, с. 117].

И действительно, современные стандарты общего образования диктуют педагогам необходимость учить детей свободно ориентироваться и принимать решения в вероятностной ситуации. То есть, уметь извлекать, анализировать и правильно обрабатывать информацию, принимать обоснованные решения в ситуациях со случайными исходами. Ориентация на демократические принципы мышления, вариативность развития событий, на формирование способности жить и плодотворно работать в сложном, постоянно меняющемся мире, требует развития нового, вероятностно – статистического, мышления у современных подростков. Эта задача может быть решена в школьном курсе математики на базе тематических блоков, связанных с описательной статистикой и элементами математического анализа, с формированием комбинаторного и вероятностного мышления [19, с. 172].

Характерной особенностью подросткового возраста является способность к экспериментированию, в том числе и в способах осуществления мыслительных операций. Школьник при осуществлении познавательной деятельности пользуется различными видами обучения, как теоретическим, та и практическим, опытным, исследовательским, экспериментальным. Подростки проявляют повышенный уровень интеллектуальной активности, обусловленной  естественной возрастной любознательностью, и стремлением  продемонстрировать свои способности окружающим, заслужить высокую оценку результатов своей деятельности. [25, c.143].

Исследования, посвященные специфике развития мышления в подростковом возрасте, показывают, что процесс познания и обучения оказывает непосредственное воздействие на развитие мышления школьника, а мышление, в свою очередь, обеспечивает формирование основных личностных компетентностей учащегося. [4, c.165].

В подростковом возрасте являются определенные новообразования в мышлении школьников: стремление к активным предметным преобразованиям и перегруппировке различных сторон изучаемого объекта, с целью всестороннего, многогранного его изучения. При этом школьники более склонны к осуществлению совместной познавательной деятельности, обучению во взаимодействии со сверстниками. Такой подход, с одной стороны, позволяет реализовать коммуникативные потребности подростка. С другой стороны – помогает подростку проверить свои умозаключения, сопоставить их с мнениями сверстников, укрепиться в собственной позиции, или принять доводы одноклассников. В любом случае, такая деятельность делает процесс развития личности, более продуктивным, так как основывается на анализе теорий, сопоставлении и сравнении мнений, синтезе собственной теории, конкретизации, формулировании умозаключений и др. Познавательная деятельность, организованная в активном, творческом, деятельном аспекте, путем эффективного взаимодействия, способствует становлению устойчивой мотивации к обучению.  [35, с.147].

 

1.2. Методические основы обучения учащихся старших классов принципам решения задач

 

Ю.М. Колягин указывал на значимую роль и место задач в процессе формирования у учащихся общей математической культуры. Автор выделил основные функции задач, и описал этапы процесса поиска решения. Ю.М. Колягин отмечал, что умение решать задачи «образует сложный комплекс, в состав которого входят активно действующие математические знания (и соответствующие им специальные умения и навыки), опыт в применении знаний и определенная совокупность сформированных свойств мышления» [15, с.152]. Автор подчеркивает, что для каждого этапа решения задачи существуют свои методические положения, соблюдение которых способствует наиболее эффективной организации работы школьников над решением задач.

При решении математических задач наиболее важным аспектом является умение определять тип задачи и действовать по алгоритму.

В обобщенном виде алгоритм решения можно представить в виде схемы:

 

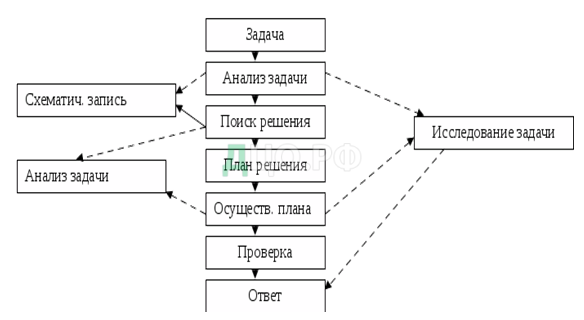
Основным моментом в обучении школьников способам решения различного рода задач выступает наличие у них мотивации к деятельности. Другими словами, содержание задачи должно быть актуальным, интересным для ученика, вызывать стремление найти решение. Особенно привлекательными для школьников выступают нестандартные задачи, задачи- шутки, мифологические сюжеты и т.д. В то же время наибольший интерес вызывают задачи, имеющие непосредственную связь с жизнью, развивающие умение находить правильные решения в жизненных ситуациях. Кроме того, подобные навыки пригодятся школьникам не только при изучении математики. Они формируют общую интеллектуальную компетентность, развивают творчество и логическое мышление.

Важной методической особенностью при выборе содержания задач для старшеклассников выступает выбор уровня сложности – с учетом личностно-ориентированного и дифференцированного подхода. Для того, чтобы задача вызвала интерес и желание найти решение, она должна быть не очень легкой, содержать некоторые противоречия или трудности, требующие напряжения ума. С другой стороны, эти трудности не должны быть чрезмерными. Учащийся должен чувствовать, что ему по силам найти решение. Для этого в каждой задаче должны быть элементы связи с ранее изученным.

Решение задачи должно осуществляться учениками самостоятельно. Возможна коллективная или групповая работа. Но учитель должен занимать координирующую и регулирующую роль. Он не должен сразу предлагать детям готовые формулы и решения, а может только отвечать на вопросы, возникающие у детей в ходе самостоятельных действий. Учитель координирует и направляет процесс поиска решения в нужном направлении, чтобы механизм поиска ответа стал для школьника открытием нового, которое затем закрепится в сознании и станет навыком.

Особую роль в развитии самостоятельности, креативности, творчества играют задачи, содержащие элементы теории вероятности и комбинаторики. Они требуют от ребенка нестандартного подхода к поиску решения.

Л.М. Фридман отмечал: «Для успешного решения нестандартных задач необходимо, прежде всего, уметь думать, догадываться. Но этого мало. Нужны, конечно, и знания, и опыт в решении необычных задач; полезно владеть и определенными общими подходами к решению» [34, c. 68].

Решение задачи начинается с восприятия и анализа условия. Первое, что должен обнаружить ученик – это знаком ли ему данный тип задач, на какую из ранее решенных задач похоже условие. Для этого учитель в начале изучения темы должен вооружить школьников набором вспомогательных задач, решение которых совместно отработано и разобрано по пунктам.

Понять идею и наметить пути поиска решения помогут и наводящие вопросы учителя, направляющие школьников по верному пути, актуализирующие ранее изученный материал.

Д. Пойа [26] сформулировал в своих работах основные принципы решения задач:

— изучить условие;

— вспомнить или найти родственную задачу;

— рассмотреть неизвестное;

— попытаться иначе сформулировать задачу;

— вернуться к основным определениям;

— сохранить часть условия;

— найти другие данные, вытекающие из условия, на основе которых можно бы было определить неизвестное.

В.И. Крупич [17, С.30] выделяет следующие виды поиска решения задач:

1. Перебор возможных вариантов решения посредством систематических проб.
2. Случайный поиск по случайно выбранному критерию.
3. Выборочный поиск, когда следующий ход выбирается на основании предыдущего.
4. Эвристический поиск, предполагающий упорядочивание информации путем отбрасывания неперспективных направлений.

В исследованиях Л.М. Фридмана [34] выделяет следующие направления работы по поиску решения:

— расчленение условия задачи на более простые части;

— замена задачи похожей или равносильной с помощью преобразования условия;

— введения вспомогательных элементов для сближения данных и искомых величин.

А. А. Столяр разделяет алгоритмы действий с задачами, метод решения которых еще неизвестен учащимся, и тех, в которых известен общий метод решения и нестандартных задач. [28, с.31].

При этом в первом случае стратегия решения должна быть ориентирована на самостоятельное открытие общего метода решения учеником, во втором случае первичным является поиск группы задач, аналогичных данной, которые решались ранее определенными, уже известными методами. Третий вид задач требует самостоятельного планомерного поиска решения.

Таким образом, при некоторых отличиях в подходах, большинство ученых сходятся к тому, что должен соблюдаться определенный порядок действий в решении задач. И одним из основных этапов является поиск аналогий.

В то же время, не все задачи можно решить, через цепочку ранее известных действий. Иногда решение может быть основано на предположении или «озарении» — т.н. эвристические задачи.

Для развития навыков действия с задачами основным является обучение школьников общим учебным действиям, формирование их личностной, интеллектуальной компетенции. Именно это свойство является основополагающим в решении задач по теории вероятностей.

 

Глава 2 Изучение современного состояния проблемы обучения учащихся старших в теме «Элементы теории вероятностей»

 

2.1 Базовые понятия и законы теории вероятности и особенности их представления учащимся общеобразовательной школы

 

Программный материал каждой дисциплины формируется на основе этапности усвоения знаний и формирования понятий. Математика, большей частью, наука, подчиненная логике мышления и закономерности выводов и решений. Именно здесь формируется умение работать по алгоритму и понимание взаимообусловленности всех процессов в окружающем мире. И действительно, в младших и средних классах школы все задачи и упражнения подчинены правилам и умению оперировать ими. У детей постепенно развивается логическое мышление, умение анализировать, сопоставлять, делать выводы.

Однако, к концу средней школы мышление школьников уже настроено на развитие абстрактного мышления и формирование образных представлений. Они уже способны, при помощи учителя корректировать житейские представления и обобщать личный опыт, формируя правильные представления о случайном, на основе которых далее можно вводить понятие вероятности и умение решать задачи на ее основе.

В свете требований современного общества и новых образовательных стандартов, необходимо учить детей анализировать ситуации и принимать решения в разных условиях, научить жить в вероятностной ситуации, анализировать и обрабатывать информацию, осуществлять логичные, обоснованные действия в ситуациях со случайными исходами.

Ориентация на демократические принципы мышления, на многовариантность возможного развития реальных ситуаций и событий, на формирование личности, способность жить и работать в сложном, постоянно меняющемся мире, с неизбежностью требует развития вероятностно — статистического мышления у подрастающего поколения.

Основными понятиями теории вероятности выступают:

• достоверные события;
• невозможные события;
• случайные события.

Невозможные события – это те события, которые при определенном комплексе условий определенно не наступают, если создался определенный комплекс условий. Другими словами, понимание смысла этих событий ведется методом «от обратного». Так, мы знаем, что у квадрата 4 одинаковых стороны, значит, если две стороны не равны – это не квадрат.

Случайные события – это те, вероятность наступления которых при данных условиях неопределенна. Так, при контакте с заболевшим ребенком несколько человек заболеют, а несколько – нет. То есть обязательность заражения не обусловлена наличием источника болезни.

Случайные события могут быть совместными или не совместными:

В случае несовместных событий, может наступить одно из этих них, но невозможно наступление двух или более.

Совместные события не исключают одновременного возникновения.

Достоверным событием является наступление хотя бы одного события из полного множества событий.

Классическое определение вероятности: Вероятностью P события А – называется отношение числа благоприятных исходов M к числу всех возможных исходов N.  Для события А вероятность рассчитывается по формуле:

P(A)=M/N

Независимые, противоположные и произвольные события.

События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.

Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события.

P(A)+P(B)=1  или  P(A) = 1- P(B)

Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е.

P(A+B)= P(A)+P(B)- P(A*B)

Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е.

P(A+B)=P(A)+P(B)

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.

Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае .

P(AB)= P(A)*P(B)

Если вероятность события В вычисляется в предположении, что событие А уже произошло, то такая вероятность называется условной вероятностью  события В по отношению к событию А. Обозначение: Р_А(В).

Теорема. Если события А и В являются зависимыми, то вероятность их произведения равна произведению вероятности одного из них на условную вероятность другого

P (AB) = P (A) · P_A(B)

Формула полной вероятности.

Если событие А может произойти только при выполнении одного из событий В₁, В₂, …, В_n которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

Р(А) = Р(В₁) · Р_В1(А) + Р(В₂) · Р_В2(А) + … + Р(В_n) · Р_Вn(А).

Эта формула называется формулой полной вероятности.

Формула Бернулли.

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.

Пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. p=P(A), а вероятность противоположного события (событие А не наступило) — буквой q=P(A¯)=1−p. Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

Геометрическое определение вероятности.

Классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом недостатков. Даже правильнее сказать, не недостатков, а ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:

На отрезок [0;1] наудачу бросается точка. Какова вероятность того, что она попадёт в промежуток [0,4; 0,7]?

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу P(A)=m/n (ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности.

Всё очень похоже: вероятность наступления некоторого события A в испытании равна отношению P(A)= g/G, где G– геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а g – мера, выражающая количество благоприятствующих событию A исходов. На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.

Рассмотрим событие: A – брошенная на отрезок [0;1] точка, попала в промежуток [0,4;0,7]. Очевидно, что общее число исходов выражается длиной большего отрезка: L=1-0=1, а благоприятствующие событию A исходы – длиной вложенного отрезка: l=0,7-0,4= 0,3

По геометрическому определению вероятности:

Законы вероятности во многом универсальны. Они являются основой научной картины мира. Современные естественные науки: биология, химия, физика, социология, философия, лингвистика и другие построены и развиваются на вероятностно — статистической базе.

На современном этапе российские программы школьного образования математике стараются объединить опыт ведущих стран мира, где теория вероятности давно введена в школьную программу. Однако, в различных странах существуют разные подходы к формированию основных вероятностных представлений. Чаще всего этот материал начинает изучаться в начальной школе. Однако, по мнению ведущих отечественных педагогов и психологов такой подход не эффективен, так как мышление младшего школьника не настроено на понимание закономерности случайных событий.

Достаточно перспективным видится подход поэтапного введения и расширения элементарных представлений о теории вероятности и навыков статистического анализа эмпирических данных на протяжении всего обучения. При этом усложнение материала проводится на основе возрастных особенностей и степени освоенности предыдущих понятий. Существенную роль при этом играют задачи прикладного характера, анализ реальных жизненных ситуаций.

Специфика решения задач по теории вероятности диктуется своеобразием вероятностно-статистического материала, его тесной связью с практической деятельностью.

Целесообразным является постоянное подкрепление операций с вероятностными законами элементами комбинаторики, усвоенными в 5-6 классах.

2.2 Анализ нормативных документов

 

Изучение дисциплин и составление рабочих программ, также, как выбор содержания и структуры теоретического и практического материала по предмету диктуется современными нормативными документами, к которым относят:

— Закон РФ «Об образовании»,

— Федеральный Государственный Образовательный Стандарт,

— Базовый учебный план,

— Образовательная программа,

— Учебная программа,

— Национальная доктрина образования и др. [37]

«Законом об образовании» диктуются основные направления образовательной деятельности и ее обеспечения, основанные на требованиях современного общества. На основе этого документа построен Государственный Стандарт Образовании, который положен в основу разработки местных, региональных нормативных документов, программ и календарных планов учителя.

Федеральный Государственный Образовательный Стандарт (ФГОС) по математике для основной школы включает изучение содержательного блока «Элементы логики, комбинаторики, статистики и теории вероятностей», определяет обязательный минимум содержания обучения статистике и требования к уровню подготовки учащихся по данному курсу.[38]

К теме, изучаемой в рамках данного блока в 5-6 классах, относится: «Описательная статистика. Вероятность. Комбинаторика», в составе которой изучаются:

— Понятие о случайном событии. Достоверное и невозможное событие. Сравнение шансов.

— Представление данных в виде таблиц, диаграмм.

— Решение комбинаторных задач перебором вариантов.

— Множество, элемент множества. Пустое множество. Подмножество. Объединение и пересечение множеств.

— Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна.

В результате освоения программы учащиеся должны:

— Уметь извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным, сравнивать величины, находить наибольшие и наименьшие значения и др.

— Выполнять сбор информации в несложных случаях, организовывать информацию в виде таблиц и диаграмм.

— Приводить примеры случайных событий.

— Сравнивать шансы наступления событий.

— Выполнять перебор всех возможных вариантов для пересчета объектов или комбинаций.

— Приводить примеры конечных и бесконечных множеств. Находить объединение и пересечение конкретных множеств.

— Иллюстрировать теоретико-множественные понятия с помощью кругов Эйлера.

В 7-9 классах вводится тема «Описательная статистика», в рамках которой ученик должен:

— Извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным. Определять по диаграммам наибольшие и наименьшие данные в однородном ряду, сравнивать величины.

— Организовывать информацию в виде таблиц, столбиковых и круговых диаграмм, в том числе с помощью компьютерных программ.

— Приводить примеры числовых данных, находить средние, размах, дисперсию числовых наборов.

— Приводить содержательные примеры использования средних и дисперсии для описания данных.

В теме «Случайные события и вероятность» учащимся дается понятие о случайном опыте и случайном событии. Также рассматриваются:

— Элементарные события.

— Частота случайного события.

— Статистический подход к понятию вероятности.

— Несовместные события. Формула сложения вероятностей.

— Вероятности противоположных событий.

— Независимые события. Умножение вероятностей.

— Достоверные и невозможные события.

— Равновозможность событий.

В результате дети учатся строить классические и статистические модели теории вероятностей.

Тема «Элементы комбинаторики» учит школьников способам решения комбинаторных задач перебором вариантов.

Основным методом итоговой проверки знаний выпускников школы на сегодняшний день является Единый Государственный Экзамен. В рамках ЕГЭ предусмотрен контроль следующих разделов математики:

• Статистические характеристики.
• Навыки сбора и группировки статистических данных.
• Наглядное представление статистической информации.
• Решение комбинаторных задач путём систематического перебора возможных вариантов и правила умножения.
• Вероятность случайных событий. Предполагает умение проводить вычисление частоты события готовых статистических данных, находить вероятности случайных событий в простейших случаях.

---

1  2