Задача № 5 по разделу «Теория машин и механизмов»
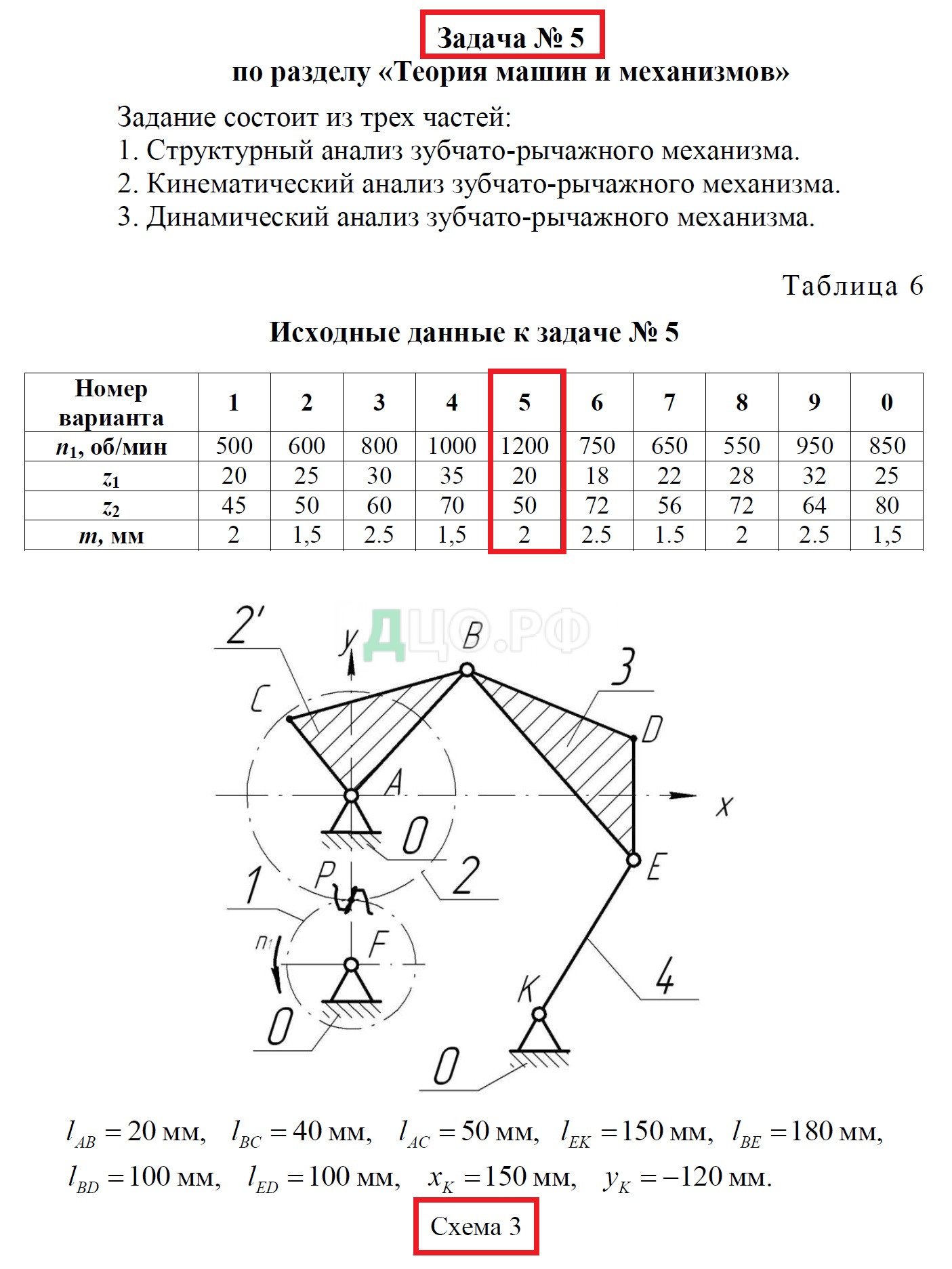
| Для заданного зубчато-рычажного механизма (рисунок 1, таблица 1) выполнить: 1. Структурный анализ зубчато-рычажного механизма. 2. Кинематический анализ зубчато-рычажного механизма. 3. Динамический анализ зубчато-рычажного механизма. Рисунок 1 – Кинематическая схема зубчато-рычажного механизма Таблица 1 – Исходные данные
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Задача 5, Вариант 5 | |||||||||||||||||||||||||||||||||||||||||||||||||
| Изм | Лист | № докум | Подпись | Дата | |||||||||||||||||||||||||||||||||||||||||||||
| Разраб. | Исследование зубчато-рычажного механизма | Лит | Лист | Листов | |||||||||||||||||||||||||||||||||||||||||||||
| Провер. | 1 | 28 | |||||||||||||||||||||||||||||||||||||||||||||||
| ТПУ | |||||||||||||||||||||||||||||||||||||||||||||||||
| Н. контр | |||||||||||||||||||||||||||||||||||||||||||||||||
| Утв. | |||||||||||||||||||||||||||||||||||||||||||||||||
Формат А4
1 Структурный анализ зубчато-рычажного механизма
Условные обозначения звеньев зубчато-рычажного механизма приведены в таблице 1.1. В таблице 1.2 приведены кинематические пары зубчато-рычажного механизма, их обозначение на схеме, класс и название.
Таблица 1.1 − Характеристика звеньев зубчато-рычажного механизма
| Звено | Схема | Название звена | Движение звена |
| 0 | Стойка | Неподвижное | |
| 1 | Шестерня − ведущее звено | Вращательное | |
| 2 | Зубчатое колесо − кривошип | Вращательное | |
| 3 | Шатун | Плоско- параллельное | |
| 4 | Коромысло | Вращательное | |
| Число подвижных звеньев n = 4 и одно неподвижное звено – стойка 0 | |||
Степень подвижности плоского зубчато-рычажного механизма по формуле П.Л. Чебышева:
W = 3n − 2p − p = 3∙4 − 2∙5 − 1 = 1, (1.1)
где n − число подвижных звеньев механизма, n = 4 (таблица 1.1);
p − число кинематических пар пятого класса, p = 5 (таблица 1.2);
p − число кинематических пар четвертого класса, p = 1 (таблица 1.2).
Соответственно с W = 1, механизм имеет одно входное звено − шестерня 1. Пассивных звеньев и кинематических пар механизм не содержит.
Составим структурные группы механизма, определим их класс и порядок (таблица 1.3).
Таблица 1.2 − Характеристика кинематических пар зубчато-рычажного механизма
| Схема | Обозна- чение | Звенья, образующие пару | Степень подвиж- ности | Класс | Тип и вид |
| В | Стойка 0, шестерня 1 | 1 | 5 | Низшая, вращательная | |
| ВП | Шестерня 1, кривошип 2 | 2 | 4 | Высшая, вращательно- поступательная | |
| В | Стойка 0, кривошип 2 | 1 | 5 | Низшая, вращательная | |
| В | Кривошип 2, шатун 3 | 1 | 5 | Низшая, вращательная | |
| В | Шатун 3, коромысло 4 | 1 | 5 | Низшая, вращательная | |
| В | Стойка 0, коромысло 4 | 1 | 5 | Низшая, вращательная |
Таблица 1.3 − Структурный состав зубчато-рычажного механизма
| Схема | Название, класс, порядок, вид, подвижность W | Чис-ло звень-ев | Число кинемати- ческих пар | Формула строения | |
| Все- го | Поводко- вых | ||||
| Начальный вращательный механизм I класса W = 3∙1−2∙1 = 1 | 1 | 1 | − | В | |
| Однозвенная двухповодковая группа с высшей кинематической парой W=3∙1−2∙1−1=0 | 1 | 2 | 2 (ВП; В) | [ВП− В] | |
| Двухзвенная двухповодковая группа II класса, второго порядка, первого вида W = 3∙2−2∙3 = 0 | 2 | 3 | 2 (В; В) | [В− В−В] | |
| Начальных механизмов − 1. Структурных групп Ассура − 2, соединение групп − последовательное. Механизм второго класса. Формула строения: в общем виде − 1−[2]−[3−4]; в развернутом − В−[ВП−В]−[В−В−В]. | |||||
2 Кинематический анализ зубчато-рычажного механизма
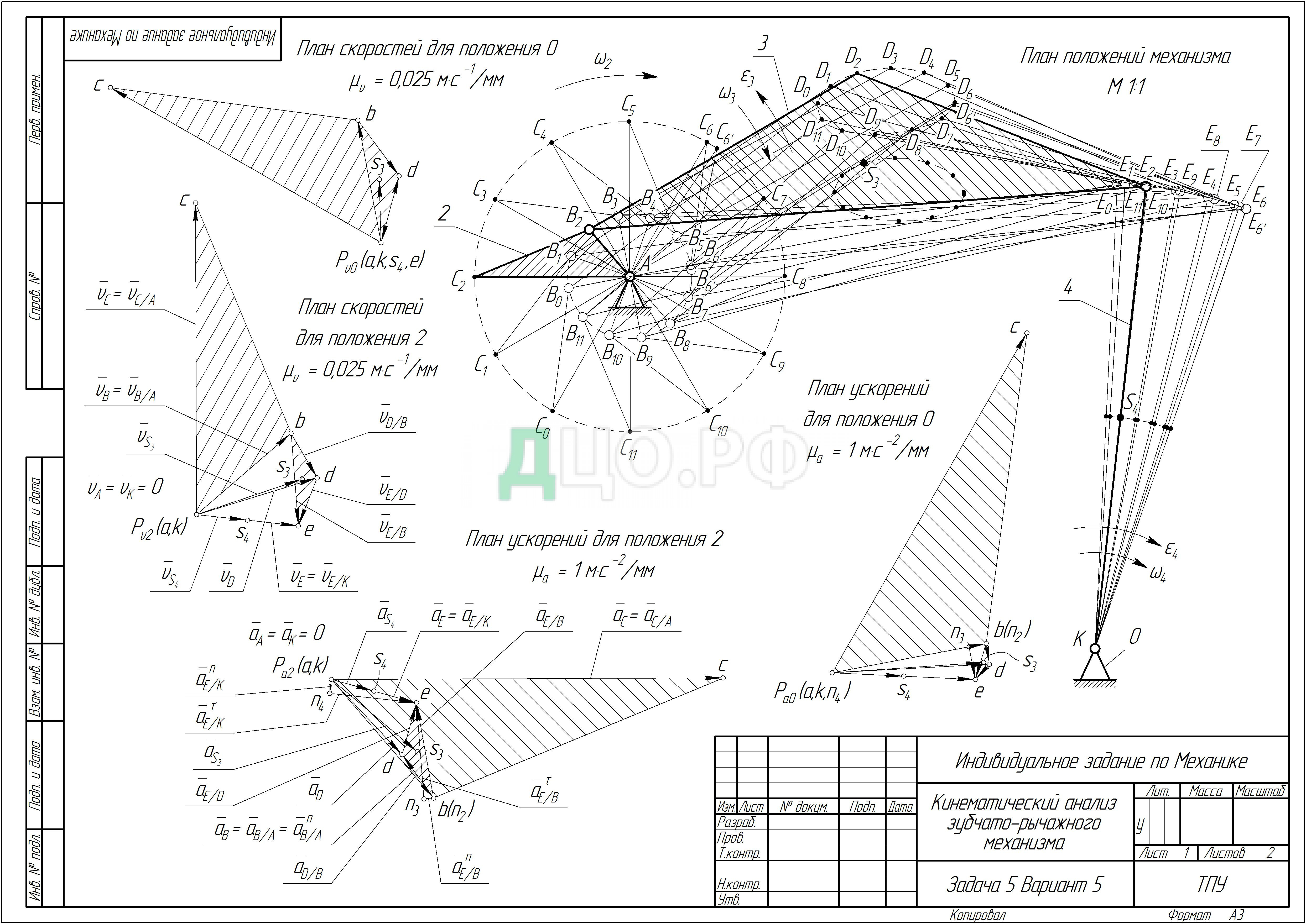
2.1 Построение плана положений механизма
Радиусы делительных окружностей зубчатых колес:
мм; (2.1)
мм, (2.2)
где m – нормальный модуль зубчатой передачи, m = 2 мм (ГОСТ 9563−80);
z1 – число зубьев ведущей шестерни 1, z1 = 20;
z2 – число зубьев ведомого колеса 2, z2 = 50.
Масштабный коэффициент длины для построения плана положений механизма:
μ = ABAB;\s\up(¯¯ = = 0,001 , (2.3)
где l − действительная длина кривошипа 2, l = 0,02 м;
− величина отрезка изображающего длину кривошипа 2 на чертеже, принимаем = 20 мм.
Расчет величин отрезков, изображающих в масштабе μ действительные размеры механизма, производим в таблице 2.1.
Таблица 2.1 − Величины отрезков, изображающих в масштабе μ
действительные размеры механизма
| Параметр | l | l | l | l | l | l | l | l | x | y | r | r |
| l, м | 0,02 | 0,04 | 0,05 | 0,18 | 0,1 | 0,1 | 0,15 | 0,075 | 0,15 | −0,12 | 0,02 | 0,05 |
| , мм | 20 | 40 | 50 | 180 | 100 | 100 | 150 | 75 | 150 | −120 | 20 | 50 |
Построение плана положений звеньев механизма производим методом планов в последовательности, определяемой формулой строения механизма.
В масштабе 1:1 строим планы механизма, начиная с построения положений ведущего звена − кривошипа AB. Наносим на чертеже произвольную точку A, которая является центром вращения кривошипа 2. Затем проводим окружность радиуса AB = 20 мм и отмечаем на ней 12 положений точки B (B, B, …, B) через каждые 30º, начиная с положения 0. Начало отсчета положений кривошипа (нулевое положение) принимаем, когда кривошип AB и шатун BE находятся на одной линии − это левое крайнее положение коромысла 4. Положения кривошипа AC = 50 мм расположены под углом 49,458º против часовой стрелки к соответствующим положениям кривошипа AB. Соединив точки B и C, получаем положения треугольника ABC кривошипа 2. Положения остальных звеньев механизма, соответствующие заданным положениям ведущего звена ABC, определяем методом засечек.
По заданным координатам, относительно центра вращения A кривошипа 2, определяем на чертеже положение неподвижной точки K(150;−120) коромысла 4. Для определения положений точки E из точки K проводим дугу окружности радиуса KE = 150 мм, а из точки B проводим дугу окружности радиуса BE = 180 мм. На пересечении дуг окружностей радиусами BE (BE, BE, …, BE) и KE (KE, KE, …, KE) определяем положения точки E (E, E, …, E). Соединив точку E (E, E, …, E) с точками B (B, B, …, B) и K, получим положения звеньев структурной группы 3−4. Положения шатуна BD = 100 мм расположены под углом 25,842º против часовой стрелки к соответствующим положениям шатуна BE. Соединив точки E и D, получаем положения треугольника BED шатуна 3. Соединив последовательно полученные точки D, D, …, D плавной кривой, получим шатунную кривую точки D шатуна 3 за один оборот кривошипа 2. Для каждого положения треугольника BED шатуна 3, на пересечении медиан, определяем положения точки S. Соединив последовательно полученные точки S плавной кривой, получим шатунную кривую центра масс S шатуна 3 за один оборот кривошипа 2.
2.2 Построение планов скоростей
Определение скоростей точек звеньев механизма производим методом планов в последовательности, определяемой формулой строения механизма.
Передаточное число зубчатой передачи:
(2.4)
Угловая скорость ведущей шестерни 1:
ω = = = 125,664 рад/с, (2.5)
где n − частота вращения ведущей шестерни 1, n = 1200 об/мин.
Угловая скорость кривошипа 2:
ω = = = 50,265 рад/с. (2.6)
Определим скорость точки B, принадлежащей начальному звену 2. Рассмотрим движение точки B относительно точки A, принадлежащей стойке 0. Запишем уравнение в векторной форме:
= + , (2.7)
где − вектор абсолютной скорости движения точки A, принадлежащей неподвижной стойке кривошипа 2, u = 0;
− вектор относительной скорости движения точки B, во вращательном движении кривошипа 2, относительно неподвижной стойки A, направленный перпендикулярно кривошипу AB.
Абсолютная скорость точки B кривошипа 2:
u = u = ωl = 50,265∙0,02 = 1,005 м/с. (2.8)
Абсолютная скорость точки C кривошипа 2:
u = ωl = 50,265∙0,05 = 2,513 м/с. (2.9)
Скорость точки B кривошипа 2 будет одинаковой для всех положений механизма. Последовательность построения плана скоростей рассмотрим на примере для положения 2.
Принимаем масштаб построения плана скоростей:
μ = 0,025 . (2.10)
Длина вектора линейной скорости точки B на плане скоростей:
u¯¯ = = = 40,2 мм. (2.11)
Из точки P, принятой за полюс плана скоростей, откладываем, в направлении вращения кривошипа, вектор скорости точки B кривошипа 2, u¯¯ ^ AB, длинной u¯¯ = 40,2 мм.
Длина вектора линейной скорости точки C кривошипа 2:
u¯¯ = u/μ = 2,513/0,025 = 100,53 мм. (2.12)
Из полюса P, в направлении вращения кривошипа, откладываем вектор скорости точки C кривошипа 2, u¯¯ ^ AC.
Определим скорость точки E, принадлежащей группе Ассура 3−4 первого вида. Рассмотрим движение точки E относительно точек B и K. Запишем уравнения в векторной форме, которые решим графически:
\s\up12( \o(u;¯E (2.13)
где − вектор абсолютной скорости движения точки B, принадлежащей кривошипу 2 (см. выше);
− вектор относительной скорости движения точки E, во вращательном движении шатуна 3 относительно точки B, направленный перпендикулярно шатуну BE;
− вектор абсолютной скорости движения точки K, принадлежащей неподвижной стойке коромысла 4, u = 0;
− вектор относительной скорости движения точки E, во вращательном движении коромысла 4 относительно стойки K, направленный перпендикулярно коромыслу KE.
Согласно первому уравнению (2.13) через точку b, на плане скоростей, проводим прямую перпендикулярную шатуну BE, а согласно второму − через полюс P (т.к. в полюсе скорости равны нулю, а u = 0) проводим прямую перпендикулярную коромыслу KE. Пересечение этих прямых определяет положение точки e, изображающей на плане скоростей конец векторов относительной скорости и абсолютной скорости , для положения 2:
u = ∙μ = 29,94∙0,025 = 0,749 м/с; (2.14)
u = u = u¯¯∙μ = 32,98∙0,025 = 0,825 м/с. (2.15)
Для определения скорости точки D шатуна BD воспользуемся теоремой подобия:
= ∙ = 29,94∙ = 16,64 мм. (2.16)
На плане скоростей относительно вектора , под углом 25,842º против часовой стрелки, от точки b откладываем отрезок , длиной 16,64 мм. Соединив полюс P с точкой d, получаем вектор u¯¯ = 40,63 мм. Тогда, абсолютная скорость точки D шатуна BD:
u = u¯¯∙μ = 40,63∙0,025 = 1,016 м/с. (2.17)
Соединив точки e и d на плане скоростей, получаем треугольник bed подобный треугольнику BED шатуна 3 на плане положений и повернутый относительно него на угол 90º.
Для определения скорости центра масс S шатуна 3 на плане скоростей определим точку s, расположенную на пересечении медиан треугольника ebd. Соединив полюс P с точкой s, получаем вектор u3 = 35,93 мм. Тогда, абсолютная скорость центра масс S шатуна 3:
u = u3∙μ = 35,93∙0,025 = 0,898 м/с. (2.18)
Скорость центра масс S коромысла KE определяем на основании теоремы о подобии:
u4 = u¯¯∙KS\s\do(4¯¯ = 32,98∙ = 16,49 мм. (2.19)
На плане скоростей отложим, на векторе u¯¯ от полюса P, вектор u4, длиной 16,49 мм, изображающий в масштабе μ абсолютную скорость центра масс S коромысла KE:
u = u4∙μ = 16,49∙0,025 = 0,412 м/с. (2.20)
Все векторы, выходящие из полюса P на плане скоростей, изображают абсолютные скорости, а отрезки, соединяющие концы векторов − относительные скорости точек механизма. В указанной последовательности производим построение планов скоростей для всех 12 положений механизма. Величины отрезков, изображающих в масштабе μ скорости точек звеньев механизма, сводим в таблицу 2.2. Величины линейных скоростей характерных точек механизма сводим в таблицу 2.3.
Таблица 2.2 − Величины отрезков, изображающих в масштабе μ
скорости точек звеньев механизма, мм
| № | u¯¯ | u¯¯ | u¯¯ | u¯¯ | u3 | u4 | |||
| 0 | 40,21 | 100,53 | 40,21 | 0 | 22,34 | 22,34 | 22,34 | 20,37 | 0 |
| 2 | 40,21 | 100,53 | 29,94 | 32,98 | 16,64 | 40,63 | 16,64 | 35,93 | 16,49 |
Таблица 2.3 − Линейные скорости характерных точек механизма, м/с
| № | u = u | u | u | u = u | u | u | u |
| 0 | 1,005 | 2,513 | 1,005 | 0 | 0,559 | 0,509 | 0 |
| 2 | 1,005 | 2,513 | 0,749 | 0,825 | 1,016 | 0,898 | 0,412 |
Определим угловые скорости звеньев механизма для положения 2.
Модуль угловой скорости шатуна 3:
|ω| = = = 4,159 рад/с. (2.21)
Направление угловой скорости ω определим, перенося мысленно вектор с плана скоростей, для соответствующего положения механизма, в точку E шатуна 3 и наблюдая направление поворота этого звена вокруг точки B, видим, что для положения 2 угловая скорость ω направлена по часовой стрелке.
Модуль угловой скорости коромысла 4:
|ω| = = = 5,497 рад/с. (2.22)
Направление угловой скорости ω определим, перенося мысленно вектор u¯¯ с плана скоростей, для соответствующего положения механизма, в точку E коромысла 4 и наблюдая направление поворота этого звена вокруг точки K, видим, что для положения 2 угловая скорость ω направлена по часовой стрелке.
На схеме механизма показываем направления угловых скоростей звеньев круговыми стрелками. Вычисленные таким образом величины угловых скоростей звеньев механизма сводим в таблицу 2.4. За положительное значение угловой скорости ω принято вращение звена против часовой стрелки.
Таблица 2.4 − Угловые скорости звеньев механизма, рад/с
| № | ω | ω | ω | ω | ω |
| 0 | 0 | 125,664 | −50,265 | −5,585 | 0 |
| 2 | 0 | 125,664 | −50,265 | −4,159 | −5,497 |
2.3 Построение планов ускорений
Определение ускорений точек звеньев механизма производим методом планов в последовательности, определяемой формулой строения механизма.
Определим ускорение точки B, принадлежащей начальному звену 2. Рассмотрим движение точки B относительно точки A, принадлежащей стойке 0. Запишем уравнение в векторной форме:
= + \s\up( nB/A + \s\up( τB/A, (2.23)
где − вектор абсолютного ускорения движения точки A, принадлежащей неподвижной стойке кривошипа 2, a = 0;
\s\up( nB/A − вектор нормального ускорения движения точки B, во вращательном движении кривошипа 2, относительно неподвижной стойки A, направленный параллельно кривошипу AB от точки B к точке A
nB/A = ω22l = 50,265∙0,02 = 50,532 м/с; (2.24)
\s\up( τB/A − вектор касательного ускорения движения точки B, во вращательном движении кривошипа 2 относительно неподвижной стойки A, направленный перпендикулярно кривошипу AB в сторону вращения углового ускорения ε. Учитывая, что кривошип 2 вращается с постоянной угловой скоростью τB/A = 0.
Учитывая, что угловая скорость кривошипа 2 постоянная, ω = const, абсолютное ускорение точки B кривошипа AB равняется его нормальному ускорению и будет одинаковым для всех положений механизма:
a = nB/A = 50,532 м/с; (2.25)
Принимаем масштаб построения плана ускорений:
μ = 1 м·с-2/мм. (2.26)
Длина вектора абсолютного ускорения точки B кривошипа 2 на плане ускорений:
a¯¯ = = = 50,532 мм. (2.27)
Последовательность построения плана ускорений рассмотрим на примере для положения 2.
Из произвольной точки P, принятой за полюс плана ускорений, по направлению от B к A, откладываем вектор абсолютного ускорения a¯¯ параллельно AB, длиной 50,532 мм.
Для определения ускорения точки C кривошипа AC воспользуемся теоремой подобия:
= ∙ = 50,532∙ = 126,331 мм. (2.28)
На плане ускорений относительно вектора , под углом 49,458º против часовой стрелки, от точки a откладываем отрезок , длиной 126,331 мм. Соединив полюс P с точкой c, получаем вектор a¯¯ = 126,331 мм. Тогда, абсолютное ускорение точки C кривошипа AC:
a = a¯¯∙μ = 126,331∙1 = 126,331 м/с. (2.29)
Соединив точки b и c на плане ускорений, получаем треугольник abc подобный треугольнику ABC кривошипа 2 на плане положений.
Определим ускорение точки E, принадлежащей группе Ассура 3−4 первого вида. Рассмотрим движение точки E относительно точек B и K. Запишем уравнения в векторной форме, которые решим графически:
\s\up12( \o(a;¯E (2.30)
где − вектор абсолютного ускорения движения точки B, принадлежащей кривошипу 2 (см. выше);
\s\up( nE/B − вектор нормального ускорения движения точки E, во вращательном движении шатуна 3, относительно точки B, направленный параллельно шатуну BE от точки E к точке B, для положения 2
nE/B = ω23l = 4,159∙0,18 = 3,113 м/с; (2.31)
\s\up( τE/B − вектор касательного ускорения движения точки E, во вращательном движении шатуна 3, относительно точки B, направленный перпендикулярно шатуну BE в сторону вращения углового ускорения ε;
− вектор абсолютного ускорения движения точки K, принадлежащей неподвижной стойке коромысла 4, a = 0;
\s\up( nE/K − вектор нормального ускорения движения точки E, во вращательном движении коромысла 4, относительно точки K, направленный параллельно коромыслу KE от точки E к точке K, для положения 2
nE/K = ω24l = 5,497∙0,15 = 4,533 м/с; (2.32)
\s\up( τE/K − вектор касательного ускорения движения точки E, во вращательном движении коромысла 4, относительно точки K, направленный перпендикулярно коромыслу KE в сторону вращения углового ускорения ε.
Отрезок, изображающий на плане ускорений в масштабе μ вектор нормального ускорения точки E шатуна 3:
3¯¯ = nE/B/μ = 3,113/1 = 3,11 мм. (2.33)
Отрезок, изображающий на плане ускорений в масштабе μ вектор нормального ускорения точки E коромысла 4:
a4 = nE/K/μ = 4,533/1 = 4,53 мм. (2.34)
В соответствии с первым векторным уравнением (2.30) на плане ускорений через точку b проводим прямую параллельную шатуну BE и откладываем на ней в направлении от точки E к точке B отрезок 3¯¯ длиной 3,11 мм. Через точку n проводим прямую перпендикулярную шатуну BE. Согласно второму векторному уравнению (2.30) через полюс P (т.к. в полюсе ускорения равны нулю, а a = 0) проводим прямую параллельную коромыслу KE и откладываем на ней в направлении от точки E к точке K отрезок a4 длиной 4,53 мм. Через точку n проводим прямую перпендикулярную коромыслу KE. Пересечение прямых и определяет положение точки e, изображающей на плане ускорений конец векторов касательных ускорений \s\up( τE/B и \s\up( τE/K, для положения 2:
τE/B = ∙μ = 31,04∙1 = 31,036 м/с; (2.35)
τE/K = ∙μ = 28,14∙1 = 28,137 м/с. (2.36)
Относительное ускорение точки E шатуна 3 определим графически, решив векторное уравнение:
= \s\up( nE/B + \s\up( τE/B. (2.37)
Соединив на плане ускорений точки b и e, получаем вектор = 31,19 мм. Тогда, относительное ускорение точки E шатуна 3:
a = ∙μ = 31,19∙1 = 31,192 м/с. (2.38)
Так как шарнир K коромысла 4 соединен со стойкой 0 (a = 0), абсолютное и относительное ускорения точки E коромысла 4 равны:
= = \s\up( nE/K + \s\up( τE/K. (2.39)
Соединив на плане ускорений полюс P с точкой e, получаем вектор
a¯¯ = 28,5 мм. Тогда, абсолютное ускорение точки E:
a = a = a¯¯∙μ = 28,5∙1 = 28,5 м/с. (2.40)
Для определения ускорения точки D шатуна BD воспользуемся теоремой подобия:
= ∙ = 31,19∙ = 17,33 мм. (2.41)
На плане ускорений относительно вектора , под углом 25,842º против часовой стрелки, от точки b откладываем отрезок , длиной 17,33 мм. Соединив полюс P с точкой d, получаем вектор a¯¯ = 33,29 мм. Тогда, абсолютное ускорение точки D шатуна BD:
a = a¯¯∙μ = 33,29∙1 = 33,293 м/с. (2.42)
Соединив точки e и d на плане ускорений, получаем треугольник bed подобный треугольнику BED шатуна 3 на плане положений.
Для определения ускорения центра масс S шатуна 3 на плане ускорений определим точку s, расположенную на пересечении медиан треугольника ebd. Соединив полюс P с точкой s, получаем вектор a3 = 36,28 мм. Тогда, абсолютное ускорение центра масс S шатуна 3:
a = a3∙μ = 36,28∙1 = 36,285 м/с. (2.43)
Ускорение центра масс S коромысла KE определяем на основании теоремы о подобии:
a4 = a¯¯∙KS\s\do(4¯¯ = 28,5∙ = 14,25 мм. (2.44)
На плане ускорений отложим, на векторе a¯¯ от полюса P, вектор a4, длиной 14,25 мм, изображающий в масштабе μ абсолютное ускорение центра масс S коромысла KE:
a = a4∙μ = 14,25∙1 = 14,25 м/с. (2.45)
Все векторы, выходящие из полюса P на плане ускорений, изображают абсолютные ускорения, а отрезки, соединяющие концы векторов − относительные ускорения точек механизма. В указанной последовательности производим построение планов ускорений для всех 12 положений механизма. Величины отрезков, изображающих в масштабе μ ускорения точек звеньев механизма, сводим в таблицу 2.5. Величины линейных ускорений характерных точек механизма сводим в таблицу 2.6.
Таблица 2.5 − Величины отрезков, изображающих в масштабе μ
ускорения точек звеньев механизма, мм
| № | a¯¯ | a¯¯ | 3¯¯ | a4 | a¯¯ | a¯¯ | a3 | a4 | ||||||
| 0 | 50,53 | 126,33 | 101,06 | 5,61 | 10,78 | 12,15 | 0 | 46,19 | 46,19 | 6,75 | 50,79 | 6,75 | 48,94 | 23,1 |
| 2 | 50,53 | 126,33 | 101,06 | 3,11 | 31,04 | 31,19 | 4,53 | 28,14 | 28,5 | 17,33 | 33,29 | 17,33 | 36,28 | 14,25 |
Таблица 2.6 − Линейные ускорения характерных точек механизма, м/с
| № | a | a | nE/B | τE/B | a | nE/K | τE/K | a = a | a | a | a |
| 0 | 50,532 | 126,331 | 5,615 | 10,778 | 12,153 | 0 | 46,193 | 46,193 | 50,786 | 48,945 | 23,096 |
| 2 | 50,532 | 126,331 | 3,113 | 31,036 | 31,192 | 4,533 | 28,137 | 28,5 | 33,293 | 36,285 | 14,25 |
Определим угловые ускорения звеньев механизма для положения 2.
Модуль углового ускорения шатуна 3:
|ε| = \s\up( τE/B = = 172,424 рад/с. (2.46)
Направление углового ускорения ε определим, перенося мысленно вектор с плана ускорений, для соответствующего положения механизма, в точку E шатуна 3 и наблюдая направление поворота этого звена вокруг точки B, видим, что для положения 2 угловое ускорение ε направлено против часовой стрелки.
Модуль углового ускорения коромысла 4:
|ε| = \s\up( τE/K = = 187,582 рад/с. (2.47)
Направление углового ускорения ε определим, перенося мысленно вектор с плана ускорений, для соответствующего положения механизма, в точку E коромысла 4 и наблюдая направление поворота этого звена вокруг точки K, видим, что для положения 2 угловое ускорение ε направлено по часовой стрелке.
На схеме механизма показываем направления угловых ускорений звеньев круговыми стрелками. Вычисленные таким образом величины угловых ускорений звеньев механизма сводим в таблицу 2.7. За положительное значение принято направление углового ускорения ε в направлении вращения против часовой стрелки.
Таблица 2.7 − Угловые ускорения звеньев механизма, рад/с
| № | ε | ε | ε | ε | ε |
| 0 | 0 | 0 | 0 | −59,879 | −307,952 |
| 2 | 0 | 0 | 0 | 172,424 | −187,582 |
3 Динамический анализ зубчато-рычажного механизма
3.1 Силы, действующие на звенья механизма
Силовой анализ механизма проводим для положения 2. Рабочим звеном данного механизма является звено 4, к которому приложено полезное (производственное) сопротивление M = 15 Н∙м. Также на механизм действуют силы тяжести, силы и моменты инерции звеньев.
Массы зубчатых колес:
кг; (3.1)
кг. (3.2)
Масса шатуна 3:
кг, (3.3)
где k – линейная плотность, для шатунов k = 8…12 кг/м;
l3 – длина шатуна 3, для треугольников l3 = 1,3lBE = 1,3·0,18 = 0,234 м.
Масса коромысла 4:
кг, (3.4)
где k – линейная плотность, для коромысел k = 10…20 кг/м.
Моменты инерции зубчатых колес относительно оси вращения:
кг·м2; (3.5)
кг·м2. (3.6)
Момент инерции шатуна 3:
кг·м2. (3.7)
Момент инерции коромысла 4:
кг·м2. (3.8)
Силы тяжести звеньев механизма:
F = mg = 0,08∙9,81 = 0,78 Н; (3.9)
F = mg = 1,25∙9,81 = 12,26 Н; (3.10)
F = mg = 2,34∙9,81 = 22,96 Н; (3.11)
F = mg = 2,25∙9,81 = 22,07 Н, (3.12)
где g − ускорение свободного падения, g = 9,81 м/с.
Величины сил инерции:
F = ma = 0,08∙0 = 0; (3.13)
F = ma = 1,25∙0 = 0; (3.14)
F = ma = 2,34∙36,285 = 84,91 Н; (3.15)
F = ma = 2,25∙14,25 = 32,06 Н. (3.16)
Моменты сил инерции звеньев механизма:
M = J|ε| = 0,000016∙0 = 0; (3.17)
M = J|ε| = 0,001563∙0 = 0; (3.18)
M = J|ε| = 0,012813∙172,424 = 2,209 Н∙м; (3.19)
M = J|ε| = 0,005062∙187,582 = 0,95 Н∙м. (3.20)
Полученные значения сил, действующих на звенья механизма в положении 2, заносим в таблицу 3.1.
Таблица 3.1 − Внешние силы, действующие на звенья механизма
| № | F | F | F | F | F | F | M | M | M |
| Н | Н∙м | ||||||||
| 2 | 0,78 | 12,26 | 22,96 | 22,07 | 84,91 | 32,06 | 15 | 2,209 | 0,95 |
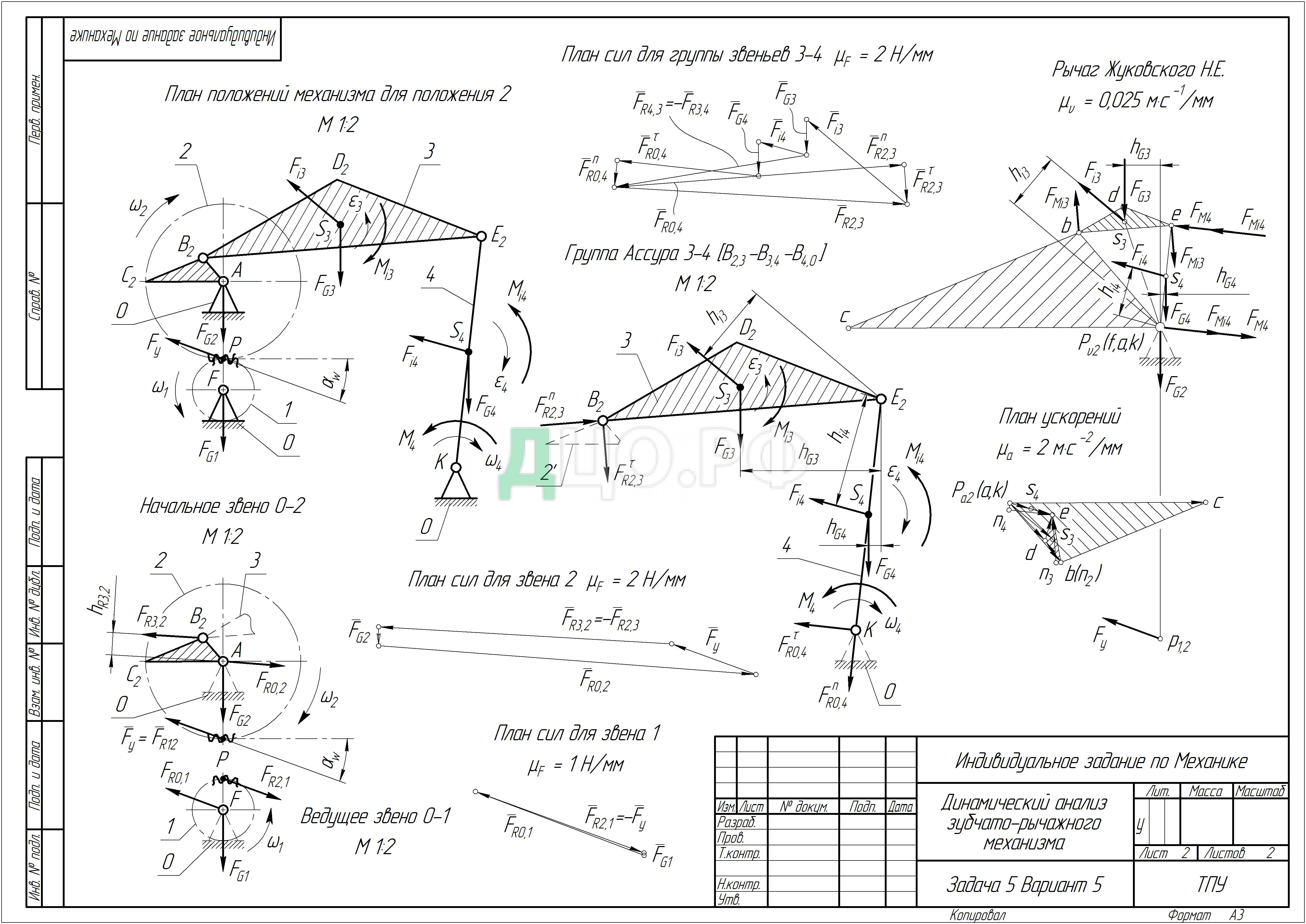
На коромысло 4 действует момент полезного сопротивления M направленный против движения коромысла. Силы тяжести ¯Gi прикладываем в центрах масс звеньев S и направляем их вертикально вниз. Силы инерции ¯ii прикладываем в центрах масс звеньев S и направляем их противоположно направлениям ускорений центров масс . Моменты сил инерции M прикладываем к соответствующим звеньям противоположно их угловым ускорениям ε.
3.2 Силовой расчет группы Ассура 3−4 первого вида
Силовой расчет начинаем с наиболее удаленной от начального звена группы Ассура II класса, состоящей из шатуна 3 и коромысла 4. В масштабе 1:2 строим схему нагружения группы звеньев 3−4, отсоединенной от остальной кинематической цепи.
К группе звеньев 3−4 приложены известные внешние силы F, F, F, F и известные внешние моменты M, M, M (см. пункт 3.1). Неизвестными являются реакции во внешних вращательных кинематических парах В и В: реакция ¯R2,3 в шарнире B, действующая на шатун 3 со стороны кривошипа 2 и реакция ¯R0,4 в шарнире K, действующая на коромысло 4 со стороны стойки 0. Реакцию ¯R2,3 разложим на две составляющие: нормальную ¯\s\up( n направленную вдоль линии BE и касательную ¯\s\up( τ направленную перпендикулярно линии BE. Также разложим на составляющие реакцию ¯R0,4: нормальную ¯\s\up( n направленную вдоль линии KE и касательную ¯\s\up( τ направленную перпендикулярно линии KE:
¯R2,3 = ¯\s\up( n + ¯\s\up( τ; (3.21)
¯R0,4 = ¯\s\up( n + ¯\s\up( τ. (3.22)
Составляющую ¯\s\up( τ определим из уравнения моментов всех сил, действующих на звено 3, относительно точки E:
ΣM = F τR2,3 − Fh + Fh − M/μ = 0, (3.23)
откуда
F τR2,3 = i3i3 = = 25,59 Н.
В результате решения уравнения (3.23) значение составляющей ¯\s\up( τ получилось со знаком плюс, что означает правильный выбор ее направления на схеме силового расчета.
Составляющую ¯\s\up( τ определим из уравнения моментов всех сил, действующих на звено 4, относительно точки E:
ΣM = −Fh + Fh − F τR0,4 + M/μ + M/μ = 0, (3.24)
откуда
F τR0,4 = i4i4 =
= = 91,71 Н.
В результате решения уравнения (3.24) значение составляющей ¯\s\up( τ получилось со знаком плюс, что означает правильный выбор ее направления на схеме силового расчета.
Уравнение равновесия всех сил, действующих на группу звеньев 3−4:
Σ¯группы 3−4 = ¯\s\up( n + ¯\s\up( τ + ¯i3 + ¯G3 + ¯i4 + ¯G4 + ¯\s\up( τ + ¯\s\up( n = 0. (3.25)
В этом уравнении неизвестными являются реакции ¯\s\up( n и ¯\s\up( n. Величины этих реакций определяем построением плана сил в масштабе μ = 2 Н/мм. В таблице 3.2 определим длину отрезков, мм, которые на плане сил будут изображать силы, указанные в векторном уравнении (3.25).
Таблица 3.2 − Силы, действующие на группу звеньев 3−4
| № | Ед. изм. | F | F nR2,3 | F τR2,3 | F | F | F=F | F | F | F τR0,4 | F nR0,4 | F |
| 2 | F, Н | 189,22 | 187,48 | 25,59 | 84,91 | 22,96 | 125,69 | 32,06 | 22,07 | 91,71 | 17,36 | 93,34 |
| , мм | 94,61 | 93,74 | 12,8 | 42,45 | 11,48 | 62,85 | 16,03 | 11,04 | 45,86 | 8,68 | 46,67 |
В соответствии с уравнением (3.25) строим план сил. Проводим линию действия реакции ¯\s\up( n и из любой точки этой линии строим известные векторы сил: ¯\s\up( τ, ¯i3, ¯G3, ¯i4, ¯G4, ¯\s\up( τ. Из конца вектора ¯\s\up( τ проводим линию действия реакции ¯\s\up( n. Точка пересечения линий действия ¯\s\up( n и ¯\s\up( n определяет их величину:
F nR2,3 = ¯\s\up( nμ = 93,74∙2 = 187,48 Н; (3.26)
F nR0,4 = ¯\s\up( nμ = 8,68∙2 = 17,36 Н. (3.27)
Соединив на плане сил начало вектора ¯\s\up( n с концом вектора ¯\s\up( τ, получим суммарную реакцию ¯R2,3 в шарнире B:
F = ¯R2,3μ = 94,61∙2 = 189,22 Н. (3.28)
Соединив на плане сил начало вектора ¯\s\up( n с концом вектора ¯\s\up( τ, получим суммарную реакцию ¯R0,4 в шарнире K:
F = ¯R0,4μ = 46,67∙2 = 93,34 Н. (3.29)
Для определения реакции ¯R4,3 = −¯R3,4 во внутренней кинематической паре В (шарнир E) рассмотрим условие равновесия шатуна 3:
Σ¯звена 3 = ¯R2,3 + ¯i3 + ¯G3 + ¯R4,3 = 0. (3.30)
Реакцию ¯R4,3 в шарнире E определяем, замыкая силовой многоугольник в соответствии с векторным уравнением (3.30), для чего на построенном плане сил конец вектора ¯G3 соединяем с началом вектора ¯R2,3:
F = ¯R4,3μ = 62,85∙2 = 125,69 Н. (3.31)
F = F = 125,69 Н. (3.32)
3.3 Силовой расчет начального звена 0−2
В масштабе 1:2 строим схему нагружения кривошипа 2, отсоединенного от остальной кинематической цепи. К кривошипу 2 приложены следующие силы: сила тяжести F, ставшая известной реакция ¯R3,2 = −¯R2,3 во вращательной кинематической паре В (шарнир B), неизвестная по модулю и направлению реакция ¯R0,2 в шарнире A и неизвестная по модулю уравновешивающая сила F, приложенная в полюсе зацепления P и направленная по линии зацепления зубчатых колес z−z.
Величину уравновешивающей силы определим из условия равновесия моментов всех сил, действующих на кривошип 2, относительно точки A:
ΣM = −Fh + Fh = 0, (3.33)
откуда
F = = = 57,84 Н.
В результате решения уравнения (3.33) значение уравновешивающей силы F получилось со знаком плюс, что означает правильный выбор ее направления на схеме силового расчета.
Реакцию ¯R0,2 в шарнире A определим из условия равновесия всех сил, действующих на кривошип 2:
Σ¯звена 2 = ¯у + ¯R3,2 + ¯G2 + ¯R0,2 = 0. (3.34)
Величину реакции ¯R0,2 определяем построением плана сил в масштабе
μ = 2 Н/мм. В таблице 3.3 определим длину отрезков, мм, которые на плане сил будут изображать силы, указанные в векторном уравнении (3.34).
Таблица 3.3 − Силы, действующие на кривошип 2
| № | Ед. изм. | F | F | F | F |
| 2 | F, Н | 57,84 | 189,22 | 12,26 | 243,98 |
| 28,92 | 94,61 | 6,13 | 121,99 |
В соответствии с уравнением (3.34) строим план сил. Из произвольной точки на чертеже строим известные векторы сил: ¯у, ¯R3,2, ¯G2. Соединив конец вектора ¯G2 с началом вектора ¯у, получим реакцию ¯R0,2 в шарнире A:
F = ¯R0,2μ = 121,99∙2 = 243,98 Н. (3.35)
3.4 Силовой расчет ведущего звена 0−1
В масштабе 1:2 строим схему нагружения шестерни 1, отсоединенной от остальной кинематической цепи. К шестерне 1 приложены следующие силы: сила тяжести F, ставшая известной реакция ¯R2,1 = −¯у в полюсе зацепления P и неизвестная по модулю и направлению реакция ¯R0,1 в шарнире F.
Реакцию ¯R0,1 в шарнире F определим из условия равновесия всех сил, действующих на шестерню 1:
Σ¯звена 1 = ¯R2,1 + ¯G1 + ¯R0,1 = 0. (3.36)
Величину реакции ¯R0,1 определяем построением плана сил в масштабе
μ = 1 Н/мм. В таблице 3.4 определим длину отрезков, мм, которые на плане сил будут изображать силы, указанные в векторном уравнении (3.36).
Таблица 3.4 − Силы, действующие на шестерню 1
| № | Ед. изм. | F | F | F |
| 2 | F, Н | 57,84 | 0,78 | 58,14 |
| , мм | 57,84 | 0,78 | 58,14 |
В соответствии с уравнением (3.36) строим план сил. Из произвольной точки на чертеже строим известные векторы сил: ¯R2,1, ¯G1. Соединив конец вектора ¯G1 с началом вектора ¯R2,1, получим реакцию ¯R0,1 в шарнире F:
F = ¯R0,1μ = 58,14∙1 = 58,14 Н. (3.37)
Результаты силового расчета механизма представлены в таблице 3.5.
Таблица 3.5 − Модули реакций в кинематических парах механизма, Н
| № | F = F | F = F = F | F = F | F = F | F = F | F = F |
| 2 | 58,14 | 57,87 | 243,98 | 189,22 | 125,69 | 93,34 |
3.5 Определение величины уравновешивающей силы методом рычага Н.Е. Жуковского
С целью проверки правильности силового расчета механизма уравновешивающую силу F определяем с помощью «жесткого рычага» Жуковского. Для этого строим в масштабе μ = 0,025 м∙с/мм, повернутый на 90º против часовой стрелки, план скоростей механизма. В одноименных точках прикладываем векторы всех внешних сил: силы тяжести F, F, F, силы инерции F, F, а также уравновешивающую силу F.
Вектор скорости в полюсе зацепления P зубчатых колес:
мм, (3.38)
где up – скорость в полюсе зацепления P, up = w2r2 = 50,265·0,05 = 2,513 м/с.
Момент силы инерции M заменим парой сил F, разнесенной по крайним точкам B и E перпендикулярно шатуну BE:
F = M/l = 2,209/0,18 = 12,27 Н. (3.39)
Момент силы полезного сопротивления M заменим парой сил F, разнесенной по крайним точкам K и E перпендикулярно коромыслу KE:
F = M/l = 15/0,15 = 100 Н. (3.40)
Момент силы инерции M заменим парой сил F, разнесенной по крайним точкам K и E перпендикулярно коромыслу KE:
F = M/l = 0,95/0,15 = 6,33 Н. (3.41)
Принимая повернутый на 90º план скоростей за рычаг, нагруженный внешними силами, составляем уравнение моментов этих сил относительно полюса P:
ΣM = −Fu¯¯cosα − F + Fh + Fh +
+ Fu¯¯ + Fu¯¯ + Fh − Fh = 0. (3.42)
Откуда определим уравновешивающую силу:
F’ = Mi3be;\s\up(¯¯ =
=
= 57,87 Н.
В результате решения уравнения (3.42) значение уравновешивающей силы F получилось со знаком плюс, что означает правильный выбор ее направления на рычаге Жуковского.
Сравним результаты определения уравновешивающей силы методом планов сил и методом рычага Н.Е. Жуковского:
ΔF = ∙100% = ∙100% = 0,05% < 5%, (3.43)
что допустимо.
Результаты сравнения уравновешивающих сил, полученные разными методами, сведем в таблицу 3.6.
Таблица 3.6 − Сравнение методов определения уравновешивающей силы
| № положения | F, Н | F’, Н | ΔF, % |
| 2 | 57,84 | 57,87 | 0,05 |
3.6 Определение величины КПД механизма
Радиусы цапф зубчато-рычажного механизма:
rF = 0,15r1 = 0,15·20 = 3 мм;
rA = 0,3lAB = 0,3·20 = 6 мм;
rB = 0,2lAB = 0,2·20 = 4 мм;
rE = 0,1lBE = 0,1·180 = 18 мм.
rK = 0,1lKE = 0,1·150 = 15 мм.
По ГОСТ 6636-69 принимаем:
rF = 3 мм; rA = 6 мм; rB = 4 мм; rE = 18 мм; rK = 15 мм. (3.45)
Моменты сил трения во вращательных кинематических парах:
Н·м;
Н·м;
Н·м; (3.46)
Н·м;
Н·м,
где f – коэффициент трения скольжения, принимаем f = 0,1.
Сила трения в зубчатом зацеплении колес:
Н. (3.47)
Мощности трения в кинематических парах:
Вт;
Вт;
Вт;
Вт;
Вт;
Вт.
Суммарная мощность трения:
= 2,136 + 7,339 + 3,504 + 0,302 + 0,77 + 4,974 = 19,025 Вт. (3.49)
Мощность, затрачиваемая на преодоление полезных (производственных) сопротивлений:
Вт. (3.50)
Мгновенное значение КПД механизма для положения 2:
Литература
- Горбенко В.Т. Теория механизмов и машин. Курсовое проектирование: учебно-методическое пособие / В.Т. Горбенко, М.В. Горбенко; Томский политехнический университет. – 3-е изд., доп. – Томск: Изд-во Томского политехнического университета, 2014. – 169 с.
- С.А.Попов. Г.А.Тимофеев. Курсовое проектирование по теории механизмов и механике машин: Учеб. Пособие для втузов / Под ред. К.В. Фролова. ‒ 2-е изд., перераб. И доп. ‒ М.: Высш. Шк., 1998. ‒ 351с.: ил.
- Теория механизмов и машин: Учеб. для втузов / К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова. ‒ М.: Высш. шк., 1987. ‒ 496 с.: ил.
Прикрепленные файлы: |
|
|---|---|

|
Администрация сайта не рекомендует использовать бесплатные работы для сдачи преподавателю. Эти работы могут не пройти проверку на уникальность. Узнайте стоимость уникальной работы, заполните форму ниже: Узнать стоимость |

|
Скачать файлы:
|
Скриншоты работы: |
|
|---|---|
|
|
|