Домашние и лабораторные работы по Информационным технологиям

Задачи: Освоить метод половинного деления, метод касательных и модифицированный метод Ньютона для решения нелинейного уравнения, научиться численно определять действительный корень нелинейного уравнения, составить алгоритм и соответствующую программу, развить практические навыки решения задач на ЭВМ.

Содержание отчета

1. Постановка задачи, исходные данные.
2. Определить с точностью относительную толщину динамического ламинарного пограничного слоя при обтекании пластины газом, используя выражения

а)  =  [3/2 – 1/2] б)  =  [2 – 2 + ],

где  – скорость газа в поперечном сечении пограничного слоя, м/с;

– скорость невозмущенного потока газа, м/с.

Сравнить полученное значение с точным.

Исходные данные: =2, =0,52, =10^-4.

методом  касательных.

2. Краткое описание метода решения нелинейных уравнений.

Метод касательных — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных.

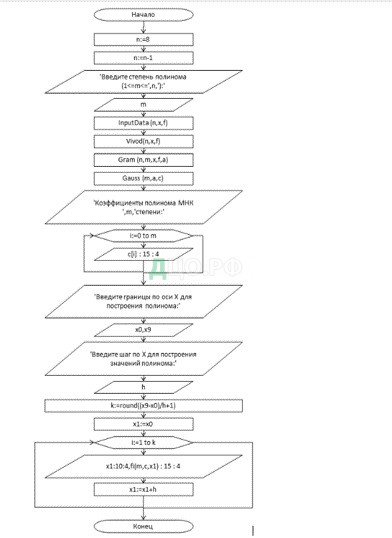
Алгоритм

1. Задается начальное приближение x₀.
2. Пока не выполнено условие остановки, в качестве которого можно взять
   |x _n+1-x _n|<или  |f'(x_n+1)|<(то есть погрешность в нужных пределах), вычисляют новое приближение:  x _n+1=x _n-f(x _n)/f'(x _n).

а)  =  [3/2 – 1/2]

Перепишем уравнение  в виде

0,52=2*(3/2x-1/2x³), подставив исходные значения

Тогда уравнение будет иметь вид

2*(3/2x-1/2x³)- 0,52=0

Упростим уравнение: 3x-2x³— 0,52=0

Введем функцию f1(х)=2*x-x*x*x-0.52;

Найдем производную функции f1(x) и обозначим f2(x):

f2(x)=f1^‘(x)= 2-3*x*x

Функция имеет две точки пересечения с осью Ох.

Цель: Изучение численных методов решения нелинейных уравнений.

Задачи: Освоить метод половинного деления, метод касательных и модифицированный метод Ньютона для решения нелинейного уравнения, научиться численно определять действительный корень нелинейного уравнения, составить алгоритм и соответствующую программу, развить практические навыки решения задач на ЭВМ.

Содержание отчета

1. Постановка задачи, исходные данные.
2. Определить с точностью относительную толщину динамического ламинарного пограничного слоя при обтекании пластины газом, используя выражения

а)  =  [3/2 – 1/2] б)  =  [2 – 2 + ],

где  – скорость газа в поперечном сечении пограничного слоя, м/с;

– скорость невозмущенного потока газа, м/с.

Сравнить полученное значение с точным.

Исходные данные: =2, =0,52, =10^-4.

методом  касательных.

2. Краткое описание метода решения нелинейных уравнений.

Метод касательных — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных.

Алгоритм

1. Задается начальное приближение x₀.
2. Пока не выполнено условие остановки, в качестве которого можно взять
   |x _n+1-x _n|<или  |f'(x_n+1)|<(то есть погрешность в нужных пределах), вычисляют новое приближение:  x _n+1=x _n-f(x _n)/f'(x _n).

а)  =  [3/2 – 1/2]

Перепишем уравнение  в виде

0,52=2*(3/2x-1/2x³), подставив исходные значения

Тогда уравнение будет иметь вид

2*(3/2x-1/2x³)- 0,52=0

Упростим уравнение: 3x-2x³— 0,52=0

Введем функцию f1(х)=2*x-x*x*x-0.52;

Найдем производную функции f1(x) и обозначим f2(x):

f2(x)=f1^‘(x)= 2-3*x*x

Функция имеет две точки пересечения с осью Ох.