1.3.1. Общие закономерности развития мышления
Исследованиями психологов (Ж. Пиаже, Дж. Брунер, А. Валлон, А.В. Запорожец, В.В. Давыдов и др.) показано, что развитие мышления ребенка происходит в направлении от наглядно-действенного к наглядно-образному и от образного к логическому. Однако трудности в определении наиболее целесообразных путей умственного развития ребенка, связаны с тем, что генетически более ранние виды мышления — наглядно-действенное и наглядно-образное — имеют двойственное значение: во-первых, они имеют собственное значение для всей последующей жизни человека, а во-вторых, подготавливают переход к следующему виду. При этом их развитие также продолжается. Подавление же этих компонентов мышления отрицательно сказывается на развитии мышления в целом. С.Л. Рубинштейн пишет: «Наглядное мышление, возникая на более ранней генетической ступени развития, чем мышление абстрактно-теоретическое, не остается затем в дальнейшем ходе развития на том элементарном, низком уровне, на котором оно первоначально находилось. В процессе общего умственного развития человека на все более высокий уровень поднимается и его наглядно-образное мышление» [36].
По мнению российских психологов, формирование каждого вида мышления и его преобладание в определенный возрастной период зависит от условий жизни ребенка, характерных для него видов деятельности, форм общения с окружающими и, что особенно важно, от форм обучения. Особенностью же детей 10–12 лет, уникальностью данного возрастного периода, является сосуществование всех трех типов мышления при ведущей роли образного мышления.
Мышление образное — процесс познавательной деятельности, направленный на отражение существенных свойств объектов (их частей, процессов, явлений) и сущности их структурной взаимосвязи. Образное мышление представляет собой единую систему форм отражения — наглядно-действенного, наглядно-образного и визуального мышления.
Опишем один эксперимент, который поможет разобраться в особенностях мышления в связи с геометрией. Эксперимент проводился с учащимися 5-го класса после того, как они изучили куб: определили форму граней, особенности расположения граней, ребер, вершин, их число, а также познакомились с разверткой куба. Все задания, предлагавшиеся учащимся в ходе эксперимента, были связаны именно с развертками куба.
Сначала учитель попросил каждого учащегося сложить куб из выданной ему развертки. С этой задачей справились все 25 учащихся класса. Далее учитель показал учащимся развертку, у которой одна из граней была заштрихована, попросил мысленно свернуть из этой развертки куб и определить, какая грань будет верхней, если заштрихованная грань — нижняя. Эта задача части учащимся оказалась не по силам, но они смогли справиться с ней после того, как такую же развертку дали им в руки. Выделим их в первую группу.
Затем учащимся было предложено аналогичное задание, но выполнить его надо было, глядя не на реальную развертку, а на рисунок в учебнике. Никто из учащихся первой группы с этим заданием не справился. Но и среди тех, кто решил предыдущую задачу, то есть выполнил мысленно преобразование предметной модели, оказались такие, что выполнить преобразование графической модели (рисунка) не смогли. Выделим их во вторую группу.
В завершение эксперимента учащимся была предложена конфигурация, изображенная на рисунке 1, и поставлен вопрос: «Является ли данная фигура разверткой куба?» Никто из учащихся первой и второй групп с заданием не справился. А остальные? Они мысленно пытались свернуть фигуру в куб и объясняли невозможность сделать это тем, что один из четырех квадратов, имеющих общую вершину, «все время перегибается», «мешается», «является лишним». Они составят третью группу. И только один учащийся свой вывод объяснил так: в каждой вершине куба должны сойтись 3 квадрата — грани куба, а здесь есть вершина, в которой 4 квадрата. Выделим его в отдельную, четвертую группу.
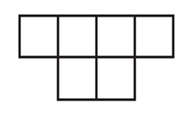
А теперь ответим на вопрос, в чем же заключаются различия в мышлении учащихся каждой из выделенных нами групп.
Мышление ребенка сначала имеет образную направленность. Оно возникает в форме наглядно-действенного мышления, основной специфической особенностью которого является неразрывная связь с практическими действиями.
Это и было характерно для учащихся первой группы. Значение этой формы мышления заключается, в частности, в том, что оно формирует такие звенья мыслительного процесса, имеющие фундаментальное значение для умственного развития ребенка, как анализ условий задачи, сопоставление полученного результата с заданным и т.д. Отметим здесь, что большое значение для развития наглядно-действенного мышления имеют графическая деятельность и конструирование.
С течением времени жизнь ставит перед ребенком новые, более сложные задачи, для решения которых необходимо осознание скрытых, существенных связей и отношений объектов и представление их в целостном организованном виде. Это требует более совершенных форм мыслительной деятельности, которые давали бы возможность преобразовать ситуацию не во внешнем, практическом, а во внутреннем, мысленном, плане. Возникает новая форма мышления — наглядно-образное мышление, являющееся способностью манипулировать образами без практических действий.
Сначала оно выступает как оперирование представлениями о конкретных предметах и их свойствах, но и в таком виде оно, теряя связь с практическими действиями, дает ребенку возможность выйти за пределы непосредственно воспринимаемого. Именно это было характерно для мышления учащихся второй группы.
Позднее образное мышление предстает в качестве способности оперировать не самими предметами, а их «заменителями»: символами, схемами, графическими моделями. Эту ступень развития мы зафиксировали на этапе исследования, когда перешли от предметной модели к графической и выделили третью группу учащихся.
Важно знать, что способность к оперированию образами не является непосредственным результатом усвоения ребенком знаний и умений. Успешный переход от наглядно-действенного к наглядно-образному мышлению зависит от уровня специально организованной деятельности, в процессе же стихийного обучения осуществляется медленно и недостаточно полно.
На основе практического и чувственного опыта у учащихся начинает развиваться логическое мышление. Оно выступает, прежде всего, в форме абстрактных понятий и суждений и дает ребенку возможность, не ограничиваясь опытом, оперировать гипотетическими утверждениями, мысленно представлять возможные случаи и делать выводы, проверяемые в дальнейшем путем эксперимента или наблюдения [3, 32].
Интересно, что логическое мышление, выходя за пределы чувственного познания, никогда полностью от него не отрывается. Существует и обратная связь: развитие логического мышления вовсе не означает, что образное мышление не способно к дальнейшему развитию, наоборот, под влиянием логического мышления оно совершенствуется и дальше. Мышление, с одной стороны, руководит и направляет деятельность, оценивает, анализирует ошибки и намечает пути их устранения, с другой стороны, обобщает ее результат и позволяет применить усвоенное действие в новых условиях.
Предпосылки такого перехода заложены в функциональной асимметрии полушарий головного мозга и сдвиге асимметрии в сторону доминирования левого полушария. Различные авторы на основании результатов исследований приходят к выводу, что в первые годы жизни у ребенка доминирует правое полушарие, дающее образное, целостное восприятие ситуации. Но начиная с десятилетнего возраста происходит сдвиг асимметрии в сторону относительного преобладания левого полушария, «отвечающего» за анализ ситуации, что становится особенно выраженным к концу подросткового возраста. Проявляется это, например, в том, что у детей 8–9 лет даже при решении арифметических задач более активизированным является правое полушарие и только между 10 и 14 годами — левое. То есть младшие школьники решают арифметические задачи каждый раз конкретно, опираясь на бытовые ассоциации, а не с помощью поиска общего способа решения, характерного для задач данного типа.
Сдвигу влево мышление ребенка обязано стимулированию «левополушарных» возможностей современной системой школьного образования, отражающей ориентацию западной цивилизации на формально-логический стиль мышления. (В восточной цивилизации, ориентированной на образность, это проявляется в меньшей степени.) Предотвратить развитие дисгармонии мышления способно изучение геометрии с опорой на образ, на эмпирическую деятельность и творческую самостоятельность.
1.3.2.Уровни развития геометрического мышления детей 10-12 лет
Под геометрическим мышлением принято понимать процесс отражения закономерностей окружающего мира, выражающих форму, величину и пространственные отношения его объектов. Оно также проходит определенные этапы в своем развитии; как правило, выделяют пять уровней развития геометрического мышления [34]. Интересующему нас возрастному периоду соответствует переход от второго из выделенных уровней к третьему.
На втором уровне (называемым «описательным») учащиеся начинают различать элементы геометрических фигур, устанавливают отношения между этими элементами и отношения между отдельными фигурами, то есть на этом уровне они способны проводить анализ воспринимаемых фигур. Это происходит в процессе наблюдения, измерения, вычерчивания, моделирования. Свойства фигур устанавливаются экспериментально, при этом они только описываются, но не определяются. Установленные свойства служат для распознавания фигур, фигуры как бы выступают носителями этих свойств. Но сами свойства еще не связываются друг с другом. Например, учащиеся замечают, что и у прямоугольника, и у параллелограмма общего вида противоположные стороны попарно равны между собой, но еще не приходят к выводу, что прямоугольник есть параллелограмм. К 6-му классу учащиеся, как правило, способны выполнить эти задачи самостоятельно, без помощи извне. Это дает основание рассматривать второй уровень развития геометрического мышления как уровень актуального развития детей этого возраста.
Зону же «ближайшего развития» составляют задачи, решаемые в совместной деятельности со взрослым, и они соответствуют третьему уровню геометрического мышления. На третьем уровне учащиеся способны установить связи между свойствами фигуры и самими фигурами; логически упорядочить свойства фигуры и сами фигуры; уяснить возможность следования одного свойства из другого. Здесь учащиеся уясняют роль определения и устанавливают логическую связь между свойствами фигуры и самими фигурами с помощью определений. На этом уровне совместно с экспериментом используются и дедуктивные методы познания, что позволяет из некоторых свойств, «добытых» экспериментально, получать другиесвойства рассуждениями. Квадрат считается прямоугольником, параллелограммом. Однако на этом уровне еще не понимается роль аксиом, дедукции, а порядок логического следования устанавливается извне – учителем, учебником и пр. [34].
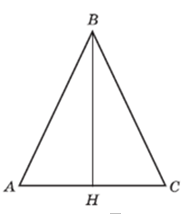
Переход от одного уровня развития геометрического мышления к другому не является биологическим процессом, а протекает под влиянием обучения, а значит, зависит от его содержания и методов. К сожалению, обучение в 1–4-х классах продолжает оставаться «длительной полосой геометрического бездействия» [34]. Этим можно объяснить тот факт, что среди учащихся, пришедших в 5-й класс, есть и такие, геометрическое развитие которых задержалось на своей первой ступени. Они воспринимают фигуру как единое целое: не видят элементов и частей фигуры, не осознают связывающих их отношений, а также отношений между фигурами, не умеют сравнивать между собой даже близкие фигуры. В геометрической фигуре они видят лишь ее форму — форма квадрата, прямоугольника и т.д. Если предложить такому ребенку перерисовать куб, изображенный на бумаге в клетку, он сначала перечертит контур изображения, а потом будет переносить отдельно каждый отрезок, расположенный внутри контура. Встречаются семиклассники, которые в простой конфигурации (рис. 2) не могут бегло переходить из внешнего треугольника во внутренний, не видят, что угол А — это угол и треугольника АВС, и треугольника АВН.
Помимо уже рассмотренных психологических особенностей детей 10–12 лет необходимо отметить еще две, недостаточно учитывающийся в практике обучения, но существенные с точки зрения обучения геометрии. В этом возрасте особое значение приобретает отмечаемая психологами интеллектуализация процессов восприятия и восприимчивость к усвоению проективных отношений.
Каждый учитель математики знает, как важно уметь «видеть» чертеж, «читать» его, от этого зависит качество усвоения геометрического содержания. И здесь недостаточно просто запомнить и воспроизвести то, что лежит на поверхности, надо увидеть содержащиеся в чертеже связи и зависимости, а это значит наполнить восприятие чертежа размышлениями. Однако данные многих исследований показывают, что часто учащиеся этого возраста не умеют всесторонне рассмотреть геометрический объект — смотрят, но не видят. Отсутствие прочных навыков восприятия задерживает развитие мышления. Более того, в процессе обучения учитель, как правило, спешит дать вербальное определение понятия без тщательной подготовки процесса его осознания, включающего восприятие. Существенно перестроить не только само восприятие, но и другие психические процессы, поднять их на более высокий уровень возможно через усвоение учащимися системы сенсорных эталонов.
Кроме собственно геометрических форм (линия, круг, квадрат, треугольник, куб, шар и пр.) эталонами выступают геометрические конфигурации (параллельные прямые, пересекающиеся прямые, смежные углы, пересекающиеся окружности и пр.) и величины (единицы длины, площади, объема, градусной меры угла). Ведь именно они помогают ориентироваться в мире геометрических объектов. Сопоставляя вновь воспринимаемые качества предметов с соответствующими элементами уже усвоенных систем сенсорных эталонов, ребенок познает свойства этих предметов, его восприятие приобретает целенаправленность и организованность.
Формирование сенсорных эталонов в основном завершается у детей в возрасте 11–12 лет. А изучение геометрии часто только начинается! Вместе с тем, декларируя развитие логического мышления в процессе изучения геометрии, и авторы учебников, и учителя подчас игнорируют тот факт, что без развития геометрического восприятия мышление формировать невозможно. Это одно из главных противоречий, мешающих развитию геометрического образования.
Второй психологической особенностью детей 10–12 лет является восприимчивость к усвоению проективных отношений. Дети этого возраста под влиянием различных видов деятельности обладают значительными возможностями в использовании разных систем отсчета. Они могут переходить от системы отсчета, связанной с собственным телом, к другим, мысленно менять позицию наблюдения. [45] Это хорошо видно на примере такого наиболее близкого к геометрии вида деятельности, как рисование. Детское рисование — спонтанная деятельность, проявляющаяся впервые со второго года жизни и утрачивающая к 13 годам спонтанный характер, претерпевает существенные за эти годы изменения. Примерно с 9 лет в рисунках появляется проекция: ребенок изображает объекты, скрытые или расположенные в глубине. Постепенно ребенок замечает, что в окружающем его мире вид предметов изменяется вместе с их отдалением от наблюдающего, и перспектива «превращается» в сходящуюся. В то же время он обращает внимание не только на то, как выглядит предмет, но и как должно выглядеть его изображение. Это спонтанное повышение графической культуры ребенка в плане создания образов и оперирования ими способствует формированию геометрических образов, однако никак не используется в практике школьного образования, тем самым не только не поспевая за развитием потенциальных возможностей ребенка, но и задерживая это развитие.
Выводы по главе 1
1) Основной целью изучения геометрии на досистематическом этапе является создание широкого круга представлений о геометрических объектах, их свойствах и основных фактах геометрии, развитие пространственного воображения, геометрической зоркости и навыков моделирования геометрических объектов. В 5–6-х классах учащийся должен накопить значительный запас геометрических знаний в виде фактов, понятий, свойств, способов действий с геометрическими объектами, которые в 7–9-х классах он будет приводить в систему, выстраивать в теорию, основанную на аксиоматическом методе и дедукции.
2) Отбор содержания и методика его изучения должны быть адекватны возрастным психологическим особенностям учащихся 5–6-х классов. Нельзя забывать и о непрерывности геометрического образования, о геометрической целесообразности и значимости. Содержание распределяется по двум линиям: геометрические фигуры и их свойства; измерение геометрических величин. Логикой изложения содержания является сочетание индуктивного подхода, основанного на приобретенном опыте, и элементов дедукции. В основе изучения содержания лежит наглядно-эмпирический метод познания. Он включает в себя визуальное и практическое изучение геометрических объектов, представленных в предметном и графическом виде, а также в виде мысленных образов. Главным же критерием усвоения содержания является умение (умение построить фигуру, описать ее свойства и т.п.).
3)Психологические особенности детей младшего подросткового возраста недостаточно учитываются при построении математического образования. Это выражается, прежде всего, в том, что геометрические объекты и изучение их свойств играют несущественную роль в математическом образовании учащихся 5–6-х классов.
4)С точки зрения путей реализации наглядно-эмпирического метода изучения геометрических объектов важными являются следующие моменты:
- графическая деятельность и конструирование продолжают оставаться приоритетными видами деятельности для учащихся 5–6-х классов;
- на развитие пространственного мышления благотворное влияние способно оказать включение в содержание обучения пространственных тел, способов их моделирования и графического изображения;
- развитие восприятия ребенка идет по пути усвоения систем сенсорных эталонов, в этой связи в процессе изучения геометрии целесообразно формировать геометрические образы, представляющие для него наибольшую значимость;»
- развитие умения мыслить образами происходит через формирование динамичности представлений, умения представлять объекты в различных пространственных положениях, изменять точку наблюдения;
- изменение отношения младших подростков к учебной деятельности, снижение интереса к учению на фоне появления новых интересов и потребностей необходимо учитывать при организации процесса изучения геометрии; разумное сочетание репродуктивных и творческих заданий, инструкций и исследований, коллективного и самостоятельного поиска должны стать принципом организации учебного процесса.
2. Наглядная геометрия как средство геометрической подготовки учащихся 5-6 классов
2.1.Анализ содержания геометрического материала учебных пособий по математике для V—VI классов
2.1.1. Содержание раздела «Наглядная геометрия» в примерных программах стандарта второго поколения
В примерных программах по математики стандарта второго поколения [33]содержание раздела «Наглядная геометрия» представлено следующим образом: наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. Четырёхугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Правильные многоугольники. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Изображение геометрических фигур и их конфигураций.
Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины.
Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Биссектриса угла.
Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Приближённое измерение площади фигур на клетчатой бумаге. Равновеликие фигуры. Разрезание и составление геометрических фигур.
Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примеры развёрток многогранников, цилиндра и конуса. Изготовление моделей пространственных фигур.
Понятие объёма; единицы объёма. Объём прямоугольного параллелепипеда, куба.
Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.
2.1.2. Анализ содержания геометрической составляющей курса математики 5-6 классов
Проведя анализ трех учебно-методических комплектов по математике для 5, 6 классов под редакцией: Г.В. Дорофеева, И.Ф. Шарыгина; Виленкина Н.Я, Жохова В.И., Чеснокова А.С. и др.; Никольского С.М., Потапова М.К., Решетникова Н.Н. и др. можно сделать следующие выводы:
- Тема «Линии» представлена во всех трех УМК, достаточно упражнений для закрепления изучаемых понятий, предлагаются контрольно-измерительные задания. Однако содержательная часть этой темы шире представлена в УМК Г.В. Дорофеева, И.Ф. Шарыгина.
- Тема «Взаимное расположение прямых» наиболее полно представлена в первом УМК. В УМК Никольского С.М. не рассматривается взаимное расположение прямых в пространстве. Во всех трех УМК представлены различные задания, большую помощь в организации обучения оказывает работа с рабочими тетрадями, которые предлагаются в УМК Г.В. Дорофеева, И.Ф. Шарыгина.
- Тема «Взаимное расположение прямой и окружности» во втором и третьем УМК не рассматривается.
- Тема «Углы» в одинаковом объеме представлена во всех трех УМК. Разница лишь в том, что в первом и втором УМК дается понятие биссектрисы угла и предложены упражнения на закрепление данного понятия.
- Тема «Многоугольники» представлена только в первом и втором УМК. К сожалению, авторы предлагают мало упражнений по данной теме.
- Тема «Треугольники и их виды наиболее полно отражена в первом и третьем УМК, а во втором УМК вводится только понятие, без классификации треугольников.
- Тема «Прямоугольники» одинаково представлена во всех трех УМК. Предлагается разнообразный дидактический материал по теме.
- Тема «Многогранники» изучается во всех трех УМК, с разницей, что в первом изучается такой многогранник, как «Пирамида», но нет понятия площади поверхности многогранника, во втором вводится понятие площади поверхности, и тема «Пирамида», а в третьем оба понятия отсутствуют.
- Тема «Симметрия» в большем объеме изучается в первом УМК. Это и изучение понятия осевой и центральной симметрий, и симметричных и центрально-симметричных фигур. В третьем УМК вводится понятие – ось симметрии и центр симметрии фигуры. Во втором УМК данная тема не представлена совсем.
- Тема «Длина окружности и площадь круга. Шар, сфера» имеет место во всех трех учебниках с разницей, что во втором и третьем УМК рассматриваются понятия: дуга окружности, шар, сфера, а в первом нет.
- В дополнительных разделах в первом УМК предлагаются темы для ознакомления: орнаменты, циклоида, треугольник Рело. Во втором: как измеряли на Руси, «Золотое сечение», построение разверток пирамиды и призмы, объем цилиндра и конуса, взаимосвязь этих величин. В третьем: единицы измерения на Руси, понятие паркет.
Геометрическая линия наиболее полно представлена в УМК Г.В. Дорофеева, И.Ф. Шарыгина. Подробнее рассматриваются многие темы. Особенно такие, как: «Линии», «Треугольник», «Симметрия». Изучение происходит не только на ознакомительном уровне. Изучаются свойства фигур.
Многие задания имеют практическую направленность, что еще раз подтверждает эффективность курса. Авторы показывают учащимся возможности применения геометрических знаний в реальной жизни.
Особое внимание хочется уделить дидактической составляющей. К каждой теме подобрано достаточно много заданий по изучаемому материалу. Предлагаются задания двух уровней сложности. Задания второго уровня чаще носят исследовательский характер.
Предлагаются задания в рабочих тетрадях. Это задания такого характера как: построить, начертить, измерить, вычислить. Некоторые задание предлагаются для развития глазомера. В дидактических материалах есть обучающие и проверочные задания по всем темам курса. Заметим, что авторы отдельное внимание уделяют интеллектуальному развитию ребенка. На это направлены знания представленные в дополнительных разделах. Авторы, познавательный материал предлагают для дополнительного изучения, тем самым, подталкивая учащегося к самостоятельной деятельности.
На основе примерных программ авторы учебников разрабатывают свои программы курса, которые являются более детальными и могут содержать дополнительные вопросы, расширяющие и углубляющие основное содержание, задаваемое стандартом.Проанализируем программу геометрическойсоставляющей курса математики 5–6-х классов, представленного в учебниках под ред. Г.В. Дорофеева и И.Ф. Шарыгина [24-25]. Перечень основных объектов изучения дан в ней по двум линиям — геометрические фигуры (их свойства и отношения) и геометрические величины — и содержит наиболее существенные аспекты их изучения. Проанализируем содержание каждой из них.
1.Геометрические фигуры
Предлагаемое содержание знакомит учащихся со следующими геометрическими понятиями:
равенство фигур — представление о равенстве как совпадении при наложении; условия равенства отрезков, углов, окружностей; построение фигуры, равной данной;
симметрия — осевая, центральная, зеркальная симметрии; равенство симметричных фигур; построение фигуры, симметричной данной относительно прямой; построение фигуры, симметричной данной относительно точки; ось и центр симметрии фигуры;
линии —замкнутые и незамкнутые линии, самопересекающиеся линии; линии на плоскости и в пространстве; ломаная;
прямая —проведение прямой с помощью линейки; бесконечность прямой; единственность прямой, проходящей через две точки; части прямой (луч, отрезок); взаимное расположение двух прямых на плоскости (параллельные и перпендикулярные прямые) и в пространстве (скрещивающиеся прямые); построение параллельных и перпендикулярных прямых с помощью линейки и угольника;
окружность — радиус, диаметр, центр окружности, круга; построение окружности с помощью циркуля; взаимное расположение прямой и окружности (касательная к окружности); взаимное расположение двух окружностей; окружности на шаре; оси и центр симметрии окружности, круга;
угол — стороны и вершина угла; биссектриса угла; острый, тупой, прямой и развернутый углы; углы, образованные двумя пересекающимися прямыми;
многоугольники — стороны, вершины, углы многоугольника; диагонали многоугольника; составление паркетов из многоугольников; правильные многоугольники; симметрия правильных многоугольников;
треугольник — элементы треугольника; классификации треугольников по углам и по сторонам (равнобедренный, равносторонний, прямоугольный треугольники); зависимость между углами и сторонами треугольника; равенство углов при основании равнобедренного треугольника; симметрия равнобедренного и равностороннего треугольников; построение треугольника по трем сторонам; сумма углов треугольника;
четырехугольник —выпуклый четырехугольник; прямоугольник и квадрат; равенство углов, равенство и параллельность противоположных сторон прямоугольника; построение прямоугольника; свойства диагоналей прямоугольника; оси и центр симметрии квадрата, прямоугольника; параллелограмм общего вида; параллельность и равенство противолежащих сторон, равенство противолежащих углов параллелограмма; центр симметрии параллелограмма; построение параллелограмма; классификация параллелограммов (ромб, прямоугольник, квадрат); свойства диагоналей параллелограммов разных видов;
многогранники — грани, ребра, вершины многогранника; изображение многогранника (проекционный чертеж);
прямоугольный параллелепипед — особенности расположения и число граней, ребер и вершин параллелепипеда; измерения параллелепипеда; куб; изображение параллелепипеда; развертка куба; плоскости симметрии параллелепипеда, куба; сечения параллелепипеда, куба плоскостями, параллельными граням;
пирамида — основание, боковые грани пирамиды; число граней, ребер и вершин пирамиды; классификация пирамид; изображение пирамиды; развертка пирамиды;
шар, сфера — диаметр и радиус шара, сферы; симметрия шара; сечения шара, сферы;
цилиндр — основания, боковая поверхность цилиндра; сечения цилиндра; развертка; плоскости симметрии цилиндра;
конус — основание, боковая поверхность конуса; сечения конуса; развертка; плоскости симметрии конуса.
Предлагаемое содержание обучения дает учащимся возможность научиться распознавать основные геометрические фигуры курса, овладеть связанной с ними терминологией, навыками построения, познакомиться с некоторыми их свойствами и связанными с ними фактами геометрии.
Предлагаемое содержание обучения дает учащимся возможность расширить представления об измерении геометрических величин, научиться выполнять практические измерения, находить величины некоторых геометрических фигур:
линейные величины — понятие длины; длина отрезка, ломаной, произвольной линии; единицы длины; линейные меры, принятые в других странах, российские и иностранные меры, вышедшие из употребления; периметр многоугольника; расстояние между двумя точками; расстояние от точки до прямой; расстояние между двумя параллельными прямыми;
площадь — понятие площади; единицы измерения площади; приближенное измерение площади фигуры; правило вычисления площади прямоугольника; площадь фигуры, составленной из прямоугольников; равновеликие фигуры, равенство площадей равновеликих фигур; нахождение площади параллелограмма и треугольника путем перекраивания в прямоугольник;
объем — понятие объема; единицы объема; правило вычисления объема прямоугольного параллелепипеда; объем тела, составленного из параллелепипедов;
Угловые величины — градусная мера угла; измерение и построение углов с помощью транспортира.
2.2.Методика изучения курса « Наглядная геометрия» в системе дополнительного образования
2.2.1.Пояснительная записка курса « Наглядная геометрия»
Целью изучения в системе дополнительного математического образования» наглядная геометрия» является всестороннее развитие геометрического мышления учащихся V-VI классов с помощью методов геометрической наглядности и повышение уровня интеллектуального развития личности школьников. Изучение и применение методов геометрической наглядности в конкретной задачной и житейской ситуациях способствует развитию наглядно-действенного и наглядно-образного видов мышления.
Для достижения поставленной цели обозначим задачи курса «Наглядной геометрии»:
- обеспечивать преемственность изучения геометрического материала начальной и основной школы;
- продолжать ознакомление с геометрическими фигурами, и их изображениями на плоскости и в пространстве;
- формировать практические методы по ознакомлению со свойствами плоских фигур;
- обеспечивать базу для изучения стереометрии в старших классах;
- знакомить с историей возникновения геометрии, со значением ее в современном мире;
- развивать логическое мышление, так как логика – это искусство рассуждать, умение делать правильные выводы;
- развивать творческое мышление учащихся через решение задач исследовательского характера;
- повышать уровень пространственного воображения учащихся;
- создавать условия стимулирования интеллектуального потенциала ученика;
- расширять кругозор, в том числе по некоторым школьным предметам, пробуждать интерес к различным областям науки, искусства;
- формировать навыки работы на компьютере во время деятельности по программе курса;
- развивать умение объективно оценивать свои силы и возможности, поводить самоанализ деятельности;
- развивать способность к толерантному общению, чувство взаимовыручки;
- воспитывать ответственность, усидчивость, целеустремленность, способность к взаимопомощи и сотрудничеству.
Содержание курса «Наглядная геометрия» и методика его изучения обеспечивают развитие творческих способностей ребенка: гибкость его мышления, «геометрическую зоркость», интуицию, воображение, способность к оперированию образами, изобразительные навыки. Вместе с тем наглядная геометрия обладает высоким эстетическим потенциалом, огромными возможностями для эмоционального и культурного развития человека. Это обусловлено «геометричностью» окружающего мира, возможностью введения в курс эмоционально окрашенного материала, способствующего формированию у учащихся положительного, эмоционально-целостного отношения к предмету.
Одной из важнейших задач преподавания наглядной геометрии является вооружение учащихся геометрическим методом познания мира, а также определенным объемом геометрических знаний и умений, необходимых ученику для нормального восприятия окружающей действительности.
В ходе изучения курса учащиеся учатся различать элементы геометрических фигур, понятие о которых они на данный момент имеют. Устанавливают отношения между этими элементами и отношения между отдельными фигурами. Анализ геометрических объектов осуществляется ими в процессе и с помощью наблюдений, измерений, вычерчивания и моделирования. Сначала фигуры выступают носителями свойств, найденных экспериментально, а установленные свойства используются учащимися для распознания, описания, построения фигур. Учащиеся овладевают экспериментальными методами исследования геометрических объектов. По мере накопления знаний возникает потребность их упорядочивания, логического обоснования, поэтому постепенно совместно с экспериментом начинают выступать и логические методы исследования.
Большое значение для развития образных форм мышления имеют конструирование и изобразительная деятельность. Это виды деятельности, которые используются при организации процесса изучения геометрических объектов и закономерностей. У детей развивается способность представить результат своих действий, как в целом, так и поэтапно. Графическая деятельность, осуществляемая учащимися, весьма разнообразна. Это может быть выполнение схематического рисунка к задаче от руки, построение фигуры или конфигурации с помощью инструментов по известному алгоритму, воспроизведение заданного графического изображения, требующее самостоятельного создания алгоритма, построение изображения по описанию.
Виды конструирования, предлагаемые школьникам при изучении геометрии: изготовление моделей пространственных тел с помощью разверток или из пластилина, из мягкой проволоки. Понятно, что ни конструирование, ни графическая деятельность не состоятся без деятельности по измерению, чему также уделяется большое внимание в данном курсе.
