Важнейшим видом деятельности для развития образного мышления является наблюдение. При этом учащиеся выделяют геометрические фигуры в предметах окружающего мира, на репродукциях картин, рисунках. Они объясняют свои наблюдения, обосновывают свои действия, делают выводы, используя математические термины, развивают математическую речь.
Не последнее место в структуре процесса изучения геометрических объектов занимает воображение, характеризуемое как создание новых образов на основе заданного наглядного материала и оперирование образами. Умение мыслить образами осуществляется через представление объекта на основе заданного рисунка, проекционного чертежа, развертки или по вербальному описанию, через мысленное перемещение объекта или смену точки наблюдения, через представление проекции геометрического тела или его сечений.
Использование моделирования в процессе обучения создает благоприятные условия для формирования таких приемов умственной деятельности как абстрагирование, классификация, анализ, синтез, обобщение, что, в свою очередь, способствует повышению уровня знаний, умений и навыков школьников.
Использование информационно-коммуникационных технологий в данном курсе помогает учителю сделать уроки наглядной геометрии интересными, динамичными, высокоэффективными, и ставит на качественно новую ступень практическую деятельность учащихся на уроке.
Так как этот курс является дополнительным, то отметка в баллах не ставится. Учащийся учится оценивать себя сам, что позволяет развивать умения самоанализа и способствует развитию самостоятельности, как свойству личность учащегося.
Выявление промежуточных и конечных результатов учащихся происходит через:
практическую деятельность; самостоятельные работы; изготовление наглядных пособий; диагностику развития логического мышления, воображения, гибкости ума, пространственного представления (тесты, решение задач на сообразительность, рассмотрение различных ситуаций); зачетные работы.
Курс «Наглядная геометрия» рассчитан на 2 года и является дополнительным курсом в системе школьного геометрического образования.
Содержание курса 64 часа
Темы курса.
- Пространство и размерность. 2
- Геометрия сквозь века. 4
- Правильные многоугольники и многогранники. 5
- Куб и его свойства. 4
- Геометрические фигуры. 11
- Окружность. 8
- Тела вращения. 2
- Симметрия. 7
- Золотое сечение. 4
- Объемные тела. 10
- Измерение величин. 4
- Решение задач. 3
Пространство и размерность.
При изучении материала показывается связь абстрактных геометрических фигур с объектами окружающего мира. Прямоугольный параллелепипед рассматривается после рассмотрения модели многоэтажного дома, имеющего три параметра: длину, ширину, высоту. «Возвращаясь» в реальный мир, учащиеся находят предметы, имеющие форму параллелепипеда. Изображение дома на листе бумаги, дает представление о предметах, имеющих только два измерения – длину и ширину (двухмерное пространство). Символом двухмерного пространства является плоскость, где «живут» фигуры, имеющие два измерения – квадрат, прямоугольник, круг… Рассматривается одномерное пространство, пространство с одним измерением – длиной. Символ – прямая, «жители» — отрезки, лучи. Показывается существование фигуры, не имеющей измерения – точки.
Вводится понятие перспективы, как средства изображения трехмерного пространства на плоскости. Учащиеся знакомятся с картинами венгерского художника Виктора Вазарели, который участвовал в разработке научной теории перспективы, позволяющей «обмануть» зрение. Оговаривается об изображении линий, скрытых от взора наблюдателя, пунктиром. Учащиеся знакомятся с неоднозначными фигурами. Это и фигура Маха, и картина Э.Боринга «Леди и старуха», и невозможные объекты: треугольник Пенроуза и невозможный куб, и работы шведского архитектора О. Рутерсварда.
Геометрия сквозь века.
Изучая материал этого раздела, учащиеся совершают исторический экскурс в предмет геометрия. Узнают, что означает слово геометрия. Знакомятся с именами великих ученых, таких как Евклид, Архимед, Фалес, Пифагор и другими. Выясняют, что означает понятие измерить. Повторяют единицы измерения метрической системы мер. Знакомятся с понятием эталон. Узнают о единицах измерения на Руси. Учатся переводить одни единицы измерения в другие.
Знакомятся с одним из разделов современной геометрии – топологией. Проводят опыты с одной из геометрических поверхностей – листом Мебиуса. Также решают топологические задачи на вычерчивание фигур одним росчерком. Узнают о понятие графы. Находят закономерность существования графа.
Правильные многоугольники и многогранники.
Получив знания на уроках математики о многоугольнике, учащиеся, изучая этот раздел, узнают о правильных многоугольниках. Учатся строить некоторые правильные многоугольники.
Знакомятся с таким понятием, как паркет. Выявляют виды правильных многоугольников, из которых можно составить паркет. Изучают технологию изготовления паркетов. Учатся определять исходные фигуры паркета. Создают эскизы своих паркетов. Рассматривают паркеты Мориса Эшера. Узнают о паркете, созданным природой – пчелиных сотах.
Используя знания о правильных многоугольниках, строят развертки правильных многогранников. Конструируют некоторые из них. Например: тетраэдр, октаэдр, додекаэдр, икосаэдр. Знакомятся с различными видами многогранников (тела Платона, тела Архимеда, тела Федорова, тела Пуансо).
Куб и его свойства.
Изучив раздел «Многогранники», учащиеся подробно знакомятся с одним из представителей этого семейства — кубом. Получив модель куба, они изучают его элементы: грани – квадраты, ребра – отрезки, вершины – точки. Работают с терминологией. Учатся изображать куб, причем разными способами. Выявляют свойства куба. Работают с разверткой куба. Выясняют, что может быть одиннадцать различных разверток куба. Работая с пластилиновым кубом, узнают, что в сечении могут получаться разные геометрические фигуры. Вычисляют объем куба и площадь поверхности, предварительно познакомившись с данным понятием.
Учащиеся знакомятся с методом трех проекций. Определяют объект по его проекциям и наоборот, строят проекции объекта.
Геометрические фигуры.
В ходе изучения данного раздела учащиеся повторяют знания о уже известных им геометрических фигурах: треугольнике, квадрате, прямоугольнике. Знакомятся с новыми геометрическими фигурами – параллелограмм, ромб, трапеция. Отрабатывают навыки их построения.
Экспериментальным путем выясняют, всегда ли можно построить треугольник. В ходе решения задач на построение треугольника (по трем сторонам, по стороне и двум углам, по двум сторонам и углу между ними) совершенствуют навыки работы с линейкой и циркулем. Отдельное внимание уделяется построению прямоугольного треугольника. С помощью инструментов строятся треугольники со сторонами 3,4,5; 6,8,10. Учащиеся знакомятся с «Пифагорийскими тройками». Также рассматривается построение прямоугольного треугольника вписанного в окружность, гипотенуза которого является диаметром данной окружности. Получают информацию об аномалии, которая называется «Бермудский треугольник».
Вспоминают формулы вычисления площади квадрата и прямоугольника. В ходе практической работы находят способ вычисления площади треугольника. Учатся вычислять площади фигур, которые можно разбить на четырехугольники и треугольники.
Ребята учатся нестандартно мыслить, решая задачи о фигурах из квадратов, составленных с помощью спичек. На развитие геометрического видения учащимся предлагаются задания на разбиение целого объекта на составляющие и объединение этих составляющих в одно целое (пусть даже в пределах одной плоскости). Этому способствует популярная китайская головоломка «Танграм» и американская игра «Пентамино».
Окружность.
В ходе изучения этого раздела дается определение окружности и круга, повторяются их элементы, выясняются свойства окружности. Учащиеся учатся вычерчивать окружность от руки, делить ее на части. Вводится понятия шар и сфера. Показывается связь этих геометрических тел с предметами окружающего мира. Экспериментально вычисляется объем шара.
Опытным путем учащиеся находят длину окружности. Работают с формулами длины окружности и площади круга, изученными на уроках математики. Решают проблемный вопрос: почему люки круглые? Для этого проводят сравнения стороны квадрата и его диагонали, длины окружности и периметра квадрата. Сравнивают площади круга, треугольника, квадрата.
Отдельное занятие посвящено окружности и кругу в архитектуре. Получают представление о знаменитом китайском символе «инь и янь». Используя исторические данные, выясняют, что круг – это фигура постоянной ширины. Узнают еще об одной фигуре постоянной ширины – треугольнике Рело.
Тела вращения.
Вводятся понятия цилиндра и конуса. Рассматривается способ получения тела путем вращения плоской фигуры вокруг одной из сторон. Строится развертка поверхности цилиндра и конуса. Конструируется модель тела. Рассматривается связь данных тел с окружающим миром.
Симметрия.
С понятиями осевая и центральная симметрии учащиеся знакомы из курса математики. При изучении этого раздела они получают знания о других видах симметрии: поворотной, переносной, скользящей. Выявляют, какие виды симметрий встречаются в живой природе, в человеческом творчестве: архитектуре, декоративно-прикладном искусстве, живописи, музыке, литературе. Знакомятся с двумя видами искусства – рисование бордюра и составление орнамента. Рассматривают различные орнаменты: орнамент зодчего XVII века «Павлинье око», мозаика Эшера. Изучают архитектуру родного города через отыскание бордюров на зданиях города.
Золотое сечение.
Учащиеся раскрывают тайны «золотого сечения», узнают о существовании «золотой» точки на любом отрезке, которая обеспечивает присутствие красоты, соразмерности всех частей. Рассматривают примеры в живой и неживой природе, где встречается «золотое сечение», (в архитектуре, скульптуре, живописи, человеке, природе). Учатся правильно рисовать пятиконечную звезду и находят в ней «золотое сечение».
Объемные тела.
Изучение данного раздела способствует всестороннему развитию геометрического мышления учащихся. Систематизируются знания о геометрических фигурах и объемных телах. Закрепляются навыки вычисления объема параллелепипеда, куба. Экспериментально выводят формулу для вычисления объема цилиндра. Определяют зависимость между объемом цилиндра и конуса. Знакомятся с законом Архимеда.
Кроме этого изучение этого раздела дает возможность для эмоционального и духовного развития ребенка. Учащиеся учатся видеть знакомые им геометрические тела в реальной жизни, на фотографиях и репродукциях картин. Они создают миниатюрные конструкции на исторические, литературные и бытовые сюжеты. Создают творческие проекты, работая над которыми используют информационно-коммуникационные технологии.
Измерение величин.
В этом разделе учащиеся продолжают разговор об измерении геометрических величин, таких, как площадь, объем. Находят ответы на вопросы: что значит измерить площадь фигуры? объем тела? Решают задачи на вычисление площадей фигур и объемов тел. Знакомятся с понятием равновеликие фигуры. Узнают об игре «Танграм». Рассматривают различные способы измерения площади фигур: с помощью палетки; по формуле Пика; посредством ее перекраивания в другую, более удобную для вычисления площади.
2.2.2.Методические принципы изучения курса «Наглядная геометрия»
Сформулируем основные принципы изучения наглядной геометрии и проиллюстрируем их примерами из учебников [24-25].
Принцип первый. Содержание курса наглядной геометрии должно разворачиваться «по спирали». При этом на первом, принципиально важном этапе, знания формируются на наглядно-интуитивном уровне в ходе предметно-практической деятельности. На последующих этапах правила и алгоритмы построения возникают как обобщенное наглядно-вербальное выражение способов действий, уже освоенных на интуитивном уровне.
Хорошо известно, что успешное умственное развитие учащихся является результатом усвоения ими не каких-либо отдельных, мозаичных знаний и умений, а определенной системы, отражающей существенные связи и зависимости изучаемой области. Переход от познания отдельных внешних свойств объектов к познанию их внутренних существенных связей происходит тогда, когда формируемое представление или понятие вытекает из сформированного ранее. Системность знаний означает наличие в сознании ученика связей между отдельно изучаемыми объектами вне зависимости от той последовательности, в которой они изучаются. Линейно-концентрическое построение курса позволяет включать вновь изучаемый объект в различные связи с объектами уже известными, возвращаться к рассмотрению этого объекта на более высоком уровне знания и расширять знания о нем за счет привлечения новой информации.
Пример 1. В 5-м классе учащиеся знакомятся с двумя главными линиями на плоскости — прямой и окружностью, учатся проводить эти линии, овладевают связанной с ними терминологией. В 6-м классе они вновь возвращаются к этим геометрическим объектам и рассматривают случаи взаимного расположения двух прямых, двух окружностей, прямой и окружности. Следующий «виток» в овладении новыми знаниями об этих фигурах происходит при изучении симметрии: прямая приобретает новое качество — она предстает как ось симметрии, а конфигурация из двух окружностей равных радиусов рассматривается в качестве опорной для выполнения построений фигур с помощью циркуля и линейки.
Пример 2. Происходит постепенное расширение понятия «расстояние»: в 5-м классе учащиеся овладевают понятием расстояния между двумя точками, в 6-м классе — определяют расстояние от точки до прямой, расстояние между двумя параллельными прямыми. При этом предлагаемый подход позволяет находить расстояние между любыми двумя фигурами.
Принцип второй. Изучение геометрического объекта должно строиться на основе приоритета в качестве единицы информации образа, а не слова. Адекватное восприятие вербального определения детям 10– 12 лет, в силу несформированности необходимого уровня словесно-логического мышления, еще не доступно, поэтому формировать понятие с помощью определения, его заучивания не следует, это ничего не даст. Прежде всего нужно создать образ изучаемого объекта. Создание образа новой фигуры или конфигурации должно опираться на практические действия по ее графическому построению или предметное моделирование, а также и на имеющееся у учащихся интуитивное зрительное представление, сложившееся в результате предыдущего обучения или вытекающее из их жизненного опыта. Созданный образ, а также описание фигуры, к которому учащиеся приходят через практические действия, должен закрепиться соответствующим термином, на создание зрительного образа «работает» часто и разъяснение происхождения термина.
Зрительный образ может носить как единичный характер, так и, рассматривая в различных пространственных положениях и в разнообразных конфигурациях, может «приобрести статус» эталона. Эталоны служат опорой при восприятии новых изображений, исходными пунктами анализа конфигурации — они участвуют в первоначальном построении ориентировочного действия, приводящего к выделению свойств нового объекта. На рисунке 3 показано, как происходит включение конфигурации «смежные углы» (рис.3 а) в конфигурации «две пересекающиеся прямые» (рис. 3б) и «треугольник» (рис.3 в).
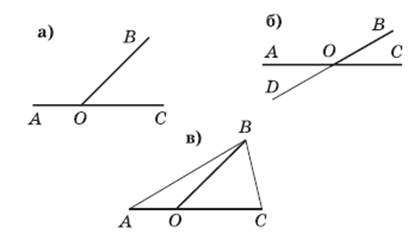
Какова же роль слова в наглядной геометрии? Образ не дает полного представления о фигуре, он лишь вводит в некоторую область, которая служит источником соответствующего понятия. Дальнейшее обучение, определяемое системой задач, должно строиться таким образом, чтобы в процессе геометрической деятельности с фигурой учащиеся раскрыли новые ее свойства, выделение среди которых существенных свойств приведет позднее к образованию понятия. Следовательно, слово выступает, во-первых, в качестве термина, фиксирующего созданный образ, во-вторых, в качестве средства общения, позволяющего описать произведенное действие или найденное свойство геометрической фигуры. Не так уж и мало для первого этапа серьезного изучения.
Пример 3. Рассмотрим процесс изучения конфигурации «две пересекающиеся прямые». Учащиеся изображают эту конфигурацию на листе бумаги и разрезают лист по проведенным прямым. Полученная предметная модель служит для изучения свойств углов, образованных пересекающимися прямыми. Накладывая углы друг на друга, составляя различные пары углов, учащиеся выделяют смежные и вертикальные углы, убеждаются в равенстве вертикальных углов, фиксируют, что смежные углы образуют развернутый угол.
Пример 4. Рассмотрим процесс изучения новой конфигурации «две параллельные прямые и секущая» (рис. 4,а) на основе уже известных — «две пересекающиеся прямые» (рис. 4,б) и «две параллельные прямые» (рис. 4,в).
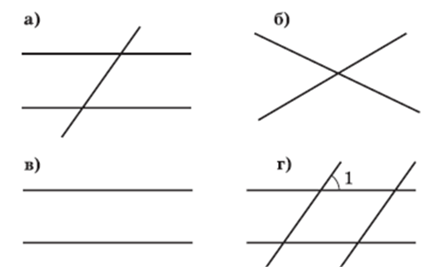
Конфигурация возникает следующим образом: «Построим несколько параллельных прямых и проведем прямую, их пересекающую. Эта прямая пересечет каждую из параллельных прямых под одним и тем же углом». Интуитивно это представление формируется, например, когда учащийся только учится писать, пользуясь тетрадью «в косую линейку»: наклон букв как раз и задается прямой, пересекающей параллельные строки.
Новое свойство данной конфигурации — сохранение углов при пересечении с параллельными прямыми — дает учащимся способ построения параллельных прямых, обогащая тем самым ранее сформированный образ новым содержанием. Существует и еще одна взаимосвязь между конфигурациями «а» и «б», она состоит в том, что первая конфигурация содержит две равные вторые. Следовательно, если учащийся может вычислить все углы между двумя пересекающимися прямыми, то он может определить величины углов, образуемых прямой при пересечении пары параллельных прямых. Чтобы указать на рисунке 2, г, все углы, равные углу 1, учащемуся необходимо оперировать тремя рассмотренными образами, последовательно выделяя их из предложенной конфигурации.
Принцип третий. Измерение геометрической фигуры должно предваряться работой, направленной на всестороннее ее изучение и осознание учащимися проблемы ее измерения, возможности или невозможности применения известных способов измерения. Таким образом, обучение геометрии будет идти от «геометрии формы» к «геометрии измерений», что соответствует установленной психологами (Ж. Пиаже, Дж. Брунер и др.) закономерности развития геометрических операций у детей — от качественных операций к количественным.
Пример 5. Знакомство, овладение основными понятиями, связанными с новой геометрической фигурой «угол», и измерение угла могут быть разделены следующим содержанием: изображение угла, изготовление моделей угла, знакомство с биссектрисой угла; классификация углов; моделирование суммы и разности двух углов. За то время, пока учащиеся выполняют соответствующие этому содержанию задания, они не только усваивают необходимую терминологию, но и осознают основные особенности новой фигуры. Переход к введению градусной меры угла целесообразен только в том случае, если учащийся, получив от учителя две модели угла, вырезанные из бумаги, и наложив один угол на другой, могут верно ответить на вопрос, какой из них больше, а какой меньше, не сбиваясь при этом на линейные размеры кусков бумаги или на их площади.
Принцип четвертый. Изучение геометрических объектов должно происходить на основе сочетания статического и динамического подходов. Необходимость усвоения детьми различных подходов к описанию рассматриваемых объектов, различных точек зрения на них подчеркивается многими исследователями. Так, Ж. Пиаже решение проблемы совершенствования знаний видел в развитии способности ребенка гибко переходить от одной точки зрения к другой (способность к децентрации), в динамизме формируемых образов.
Одним из основных свойств предметов окружающего мира является движение. Движение, динамическое развитие ситуации оказывают воздействие на развитие пространственного воображения ребенка. «Свободный переход от фиксированной в себе точки отсчета (координат) к системе со свободно перемещаемой точкой отсчета является стержнем общего развития понимания пространства» [33]. Реализация этого принципа особенно важна потому, что прослеживание «умственным взором» преобразований, совершаемых в пространстве, затрудняет многих учащихся.
С целью наиболее эффективного развития образного, пространственного мышления учащихся в систему упражнений целесообразно включать задания, содержащие такие геометрические преобразования, как параллельный перенос, поворот, центральная симметрия, осевая симметрия.
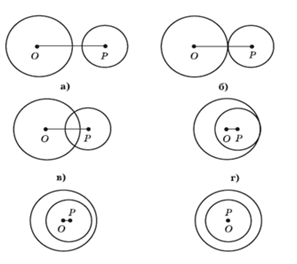
Идея движения может использоваться и как вспомогательное средство. Например, она помогает охватить единым взором все возможные случаи взаимного расположения на плоскости двух окружностей (рис. 5): окружности не пересекаются; касаются внешним образом; пересекаются; касаются внутренним образом; не пересекаются, но одна из них расположена внутри другой; отдельный случай здесь — концентрические окружности. Достаточно лишь представить, что одна окружность неподвижна, а другая движется, сначала приближаясь к ней, затем – пересекая. Все этапы движения фиксируются отдельными рисунками. Аналогичным образом можно рассмотреть и взаимное расположение прямой и окружности.
Реализация идеи движения должна осуществляется путем выполнения сначала реальных перемещений геометрических фигур, а затем — мысленных. Знакомство с отдельными видами симметрии, построение симметричных фигур основано на реальных движениях — перегибании листа бумаги, повороте на 180°, постепенно переводимых в умственный план и претерпевающих сокращения.
Пример 6. Учащиеся с помощью циркуля сначала «поворачивают» точку относительно центра на 180°, а затем подмечают, что достаточно провести через две заданные точки прямую и отложить по другую сторону от центра отрезок, равный расстоянию от центра до данной точки. Но, несмотря на то, что учащиеся «открыли» способ построения центрально-симметричной точки, вполне допустимо и выполнение реального поворота фигуры. К нему учащиеся снова возвращаются при знакомстве с параллелограммом, все свойства которого они обнаруживают при повороте параллелограмма относительно его центра симметрии.
Принцип пятый. Основным методом исследования геометрических объектов должен стать эксперимент как реальное физическое действие: наложение фигур, перегибание по оси симметрии, поворот вокруг центра симметрии и др. Опираясь на его результаты, рассмотрев и проанализировав различные частные случаи, учащиеся на основе индуктивных рассуждений выдвигают гипотезу, отражающую найденную закономерность. Следовательно, доминирующим методом познания в курсе наглядной геометрии является индукция. Дедукция имеет место в основном как переход в процессе познания от общего к частному и единичному. Например, среди многообразия пространственных форм выделяются многогранники, и дальнейшее изучение концентрируется на параллелепипеде, пирамиде, призме. Дедуктивные рассуждения — как процесс логического вывода, как способ получения знаний, противопоставляемый непосредственным наблюдениям и эксперименту — могут появляться только постепенно и параллельно с ними, проявляться локально. Таким образом можно реализовать положение, согласно которому развитие ребенка происходит в двух направлениях — и к более конкретному, и к более абстрактному (П.П. Блонский, Н.А. Менчинская и др.), а выбор пути усвоения знаний зависит от возрастных особенностей, целей обучения и от природы самого знания.
Постепенный переход к увеличению элементов дедукции дает учителю возможность, исходя из подготовленности класса, выбрать тот или иной путь изучения геометрического объекта, например, ограничиться физическим экспериментом и решать все задачи с опорой на физическое действие или увеличить долю доказательных, обосновывающих рассуждений. Для ученика такой подход означает возможность восприятия материала на доступном ему уровне, при этом он имеет возможность знакомиться и с другими вариантами решения, лежащими пока в зоне его ближайшего развития.
Пример 7. Организовав экспериментальное исследование свойства суммы углов треугольника, которое заключается в том, что каждый учащийся начертил произвольный треугольник, измерил величины его углов, нашел их сумму, а затем сравнил полученный результат с результатами своих одноклассников, учитель может предложить классу прийти к открытию этого факта путем рассуждений. Рассуждения основаны на перешедшем во внутренний план реально выполнявшемся действии по параллельному переносу прямой с помощью угольника и линейки. Перемещая мысленно прямую, на которой лежит одна из сторон треугольника, параллельно самой себе к противолежащей вершине, учащиеся «собирают» все углы треугольника в один развернутый угол (рис. 6).
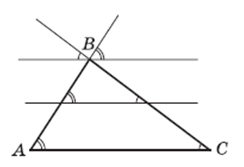
Покажем, как можно реализовать все выделенные нами положения при изучении параллелограмма. Заметим, прежде всего, что в основе рассмотрения свойств этой фигуры лежат две системы представлений: параллельность и центральная симметрия. Образ параллелограмма возникает перед учащимися в результате построения ими двух пар параллельных прямых (рис. 7).
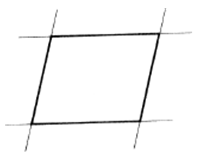
Опираясь на визуальное изучение и выполненные построения, учащиеся фиксируют внимание на том, что противоположные стороны параллелограмма параллельны. Таким образом, уже на этом этапе они имеют возможность самостоятельно изобразить его, при этом термин «параллелограмм» ассоциируется у них с параллельностью и через способ построения.
Перейдем к симметрии. И здесь нам поможет эксперимент. Параллелограмм — центрально-симметричная фигура. Опираясь на практическое действие поворота фигуры на 180°, уже знакомое учащимся по изучению этого свойства у других фигур, они открывают для себя такие свойства параллелограмма: равенство противолежащих сторон и углов; равенство треугольников, на которые делится параллелограмм диагональю; диагонали делятся в точке пересечения пополам (рис. 8).
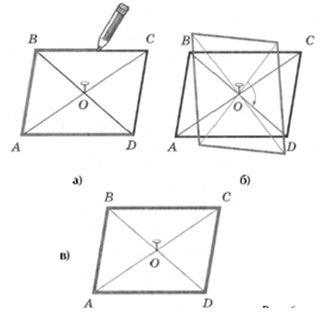
Последнее из выявленных свойств дает еще один способ изображения параллелограмма – начертить два отрезка, пересекающихся своими серединами, и последовательно соединить их концы. Кроме того, этот эксперимент позволяет сформировать динамичный образ параллелограмма, которым несложно манипулировать мысленно.
Следующий этап — знакомство с классификацией параллелограммов. Здесь учащиеся сопоставляют свойства диагоналей параллелограмма общего вида, прямоугольника, ромба, квадрата, рассматривают на предмет наличия осей симметрии, выясняют, какие из этих свойств можно использовать для их построения.
Последний шаг в изучении параллелограмма — нахождение площади параллелограмма путем перекраивания его в прямоугольник (рис. 9).
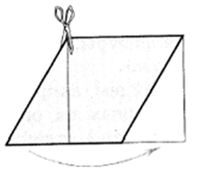
Этот фрагмент рассматривается при изучении пункта, посвященного равновеликим и равносоставленным фигурам.
2.3. Методика обучения геометрической деятельности при изучении курса «Наглядная геометрия»
Изучение геометрических фигур и пространственных отношений основывается на определенных действиях, которыми учащиеся должны овладеть. Это действия наблюдения, воображения, измерения, конструирования и графические действия.
2.3.1. Наблюдение
Развитие умения наблюдать происходит в процессе осмысленной деятельности по восприятию, рассматриванию геометрических объектов, через формирование зрительных эталонов, отражающих основные геометрические конфигурации, через знакомство с некоторыми специальными приемами, облегчающими восприятие.
Действия наблюдения составляют основное содержание задач, целью которых является:
- создание мысленного образа геометрического объекта;
- распознавание заданных конфигураций или фигур;
- сравнение непосредственно воспринимаемых объектов или групп объектов.
Создание мысленного образа геометрического объекта — это, пожалуй, ключевой момент для формирования геометрических представлений, для изучения свойств геометрических фигур. И здесь исключительно важным является то, что происходить создание образа должно в процессе правильно организованной, разнообразной деятельности по всестороннему обследованию объекта. Покажем это на следующем примере.
Пример 1. Формирование представления о прямоугольном параллелепипеде.
Может показаться, что такие представления формируются еще в дошкольном детстве, ведь это самая распространенная геометрическая фигура в окружающем мире. Но это не так. Чтобы убедиться в этом, достаточно попросить пятиклассников ответить на вопрос, сколько у куба граней. А на вопрос о числе ребер ответы будут самые разные, даже если при этом куб будет находиться у каждого в руках.
Чтобы создать образ параллелепипеда, учащимся необходимо осуществить разнообразные практические действия с моделями параллелепипеда, причем под руководством учителя, который руководил бы процессом обследования и направлял его: указанием, какие особенности необходимо выделить, называнием их и т.п. Учащимся следует, взяв модель параллелепипеда в руки (это может быть деревянный брусок, спичечный коробок, бумажная модель, склеенная из развертки, и пр.), выполнить следующие действия:
1) провести ладонью по его поверхности и ощутить, что она состоит из плоских частей;
2) рассмотреть отдельные плоские части — грани параллелепипеда, определить их форму;
3) зафиксировав противоположные грани, например, пальцами, зрительно установить их равенство;
4) зафиксировав каждую грань пальцами (тремя пальцами одной руки и тремя пальцами другой), определить число граней;
5) провести ладонью по поверхности параллелепипеда, выделив линию излома — ребро параллелепипеда; выделить грани, границам которых принадлежит это ребро; выделить и другие ребра, принадлежащие этим же граням; выделить еще несколько ребер параллелепипеда;
6) выделить группы равных ребер параллелепипеда и определить их число; обвести равные ребра карандашом одного цвета;
7) выделить вершины параллелепипеда; поместив его между ладонями, определить особенности расположения вершин;
8) зафиксировав каждую вершину одним пальцем, подсчитать их число;
9) выбрав одну из вершин, определить число ребер, сходящихся в этой вершине; сравнить длины этих ребер (на глаз; проведя по ним пальцем; измерением); проделать это для других вершин; заметить, что в каждой вершине сходятся три ребра разной длины;
10) зафиксировать внимание на гранях, сходящихся в одной вершине: их число, размеры.
В описанном исследовании используются очень разные действия. И простые тактильные действия и движения, которые «в ходу» у каждого ребенка с младенчества (например, движения руки, фиксирующие тот или иной выделяемый в данный момент элемент изучаемого объекта, акцентирующие на нем внимание; при этом способы фиксирования учащиеся могут придумывать сами). Они помогают осуществлять, направляют более сложные действия, сочетающие в себе зрительное сопоставление, сравнение и анализ отдельных элементов, определение их количественных характеристик, синтез этих элементов в единое целое и выделение ключевых особенностей исследуемого объекта.
По сути, наблюдение здесь выступает и методом исследования, так как предложенный набор действий представляет собой план систематического наблюдения. Предложите учащимся провести описанное исследование, а затем попросите рассказать о том, что они знают о параллелепипеде.
Решение задачи сравнения непосредственно воспринимаемых объектов требует от учащихся умения подмечать в рассматриваемых объектах общие черты и различия, находить среди них существенные, и служит, тем самым, формированию понятий.
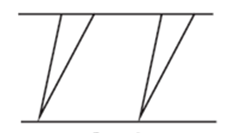
Пример 2. На рисунке 10 изображены две группы линий. Чем отличаются линии одной группы от линий другой?
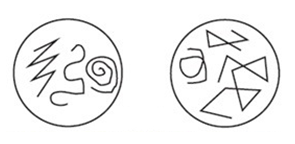
Задача сравнения в этом задании сформулирована прямо. Сравнивая линии каждой группы, учащиеся должны увидеть, что линии первой группы не имеют самопересечений, а линии второй группы — самопересекающиеся.
Пример 3. На рисунке 11 изображены два параллелограмма. Покажите, что эти параллелограммы равновелики.
Здесь задача сравнения в явном виде не сформулирована, но является сутью задачи, так как для ее решения учащимся необходимо заметить, что оба данных параллелограмма могут быть перекроены в один и тот же прямоугольник. Это и будет означать, что параллелограммы равновелики. Есть и другое решение, которое заключается в том, что один из данных параллелограммов можно перекроить в другой. Это тоже можно «увидеть» на рисунке: мысленно «отрезав» от первого параллелограмма треугольник и «приложив» его к противолежащей стороне, мы получим второй параллелограмм.
Когда перед учащимися ставиться задача распознавания геометрических объектов, то преследуют две цели — формирование законченного образа объекта изучения, его узнавание и различение в различных пространственных положениях, в более сложных конфигурациях, а также развитие у учащихся геометрической зоркости и наблюдательности.
Пример 4. Найдите на рисунке 12 прямоугольники.
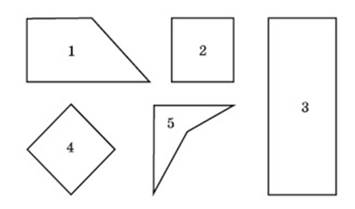
Особенность рисунка заключается в том, что он содержит две фигуры, не являющиеся прямоугольниками, а также два квадрата. Чтобы справиться с этим заданием, учащиеся должны, во-первых, помнить, что квадрат является прямоугольником, а во-вторых, увидеть квадрат, расположенный в непривычном для них положении. Особенность восприятия геометрических объектов такова, что фигура 4 воспринимается как ромб, если учащиеся знакомы с ромбом, в противном случае — как четырехугольник, не являющийся квадратом. Если учащиеся не выделяют эту фигуру как квадрат, необходимо предложить им мысленно, а в случае затруднения и практически, повернуть ее так, чтобы квадрат принял более привычное для распознавания горизонтально-вертикальное расположение.
Пример 5. Сколько треугольников изображено на рисунке 13?
Это упражнение направлено на отработку умения распознавать треугольник в более сложной конфигурации, а в данном случае и как составную часть другой фигуры, и как объединение других фигур.
