2.3.2.Воображение
Под воображением понимают операции по мысленному оперированию геометрическими образами и по созданию новых образов. Это не есть творческое воображение, создающее принципиально новые объекты, новыми эти объекты являются для учащихся, так как рождаются ими самостоятельно на основе преобразования уже известных объектов. Это воссоздающее воображение — представление новых объектов в соответствии с их описанием, чертежом, схемой.
Формируется воображение на основе восприятия, поэтому обогащая опыт восприятия, наблюдения, побуждая учащихся к созданию образов, учитель развивает их воображение. Любое сложное действие, прежде чем стать достоянием разума, должно быть реализовано вовне. Овладение действиями воображения происходит в процессе перехода практических действий во внутренний план.
Действия воображения являются содержанием задач, целью которых является:
- создание мысленного образа геометрического объекта по его описанию;
- создание мысленного объемного образа объекта на основе рисунка пространственного тела или проекционного чертежа;
- мысленное оперирование образом.
Говоря о создании мысленного образа по его описанию, будем рассматривать два случая: во-первых, когда в ходе решения задачи учащимся необходимо мысленно конструировать новый образ из знакомых образов как из элементов конструктора, во-вторых, как речь идет о геометрическом месте точек.
Приведем примеры двух заданий, где в качестве «элементов конструктора» выступают параллелепипеды.
Пример 6. Из четырех кубиков выложить параллелепипед можно двумя способами. Одинаковой ли будет площадь поверхности параллелепипеда в первом и втором случаях?
Сложить из четырех кубиков параллелепипед учащиеся должны мысленно, а вот проверить, что таких возможностей только две, мысленно довольно сложно. Сделать это необходимо, прибегнув к кубикам реальным.
Пример 7. Объем параллелепипеда равен 64 см3, ширина — 4 см, высота — 2 см. Длину этого параллелепипеда уменьшили на 3 см. Определите объем получившегося параллелепипеда.
Здесь мысленное воспроизведение ситуации позволяет найти более рациональный путь, чем последовательное вычисление длины большого параллелепипеда, уменьшение ее на 3 см и вычисление объема нового параллелепипеда. Во время поиска и обсуждения способов решения задачи учитель предлагает учащимся представить, что заданный в условии параллелепипед разрезают на два параллелепипеда, при этом длина «отрезаемого» параллелепипеда равна 3 см. Отсюда, чтобы решить задачу, необходимо объем исходного параллелепипеда уменьшить на объем «отрезанной» части.
В результате выполнения заданий на геометрические места точек учащиеся должны именно «увидеть» фигуру как множество точек, обладающих определенным свойством, как бы заставить точки слиться в единую фигуру.
Пример 8. Начертите какую-нибудь прямую и обозначьте ее буквой а. Постройте несколько точек, находящихся от прямой а на расстоянии 2 см. Где расположены все такие точки?
Выполняя построение точек, удаленных от прямой на 2 см, учащиеся сначала должны «увидеть», что точки образуют прямую, параллельную прямой а, после чего понять, что прямых, удовлетворяющих условию, две.
Задача создания мысленного образа пространственного тела на основе графического изображения решается, прежде всего, для пространственных фигур. Прежде чем познакомиться с проекционным чертежом, который используется в стереометрии, в курсе наглядной геометрии изучение пространственных фигур полезно начать с рисунков стеклянных, каркасных моделей, а также сплошных тел, сложенных из кубиков или параллелепипедов, постепенно абстрагируя изображения материальных тел и заменяя их проекционным чертежом.
Пример 9. Сколько вершин, ребер и граней у многогранника (рис. 14)?
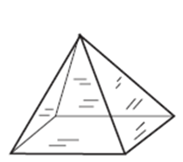
Материальный объект представить легче. Использование изображения стеклянной модели на начальном этапе овладения действиями по созданию мысленных пространственных образов и терминологией, связанной с многогранниками, позволяет учащимся «увидеть» все элементы многогранника, определить их число, особенности расположения, форму граней. На стеклянной модели видны и ребра, и грани.
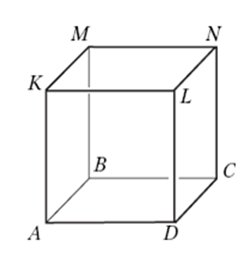
Пример 10. На рисунке 15 изображена каркасная модель куба. Назовите ребра, выходящие из вершины М.
Изображение каркасной модели имеет более абстрактный характер, поэтому его использование носит переходный характер от изображения стеклянной модели к проекционному чертежу. На каркасной модели видны ребра, а грани как бы прозрачны, реально не видимы.
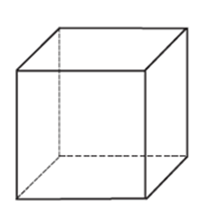
Пример 11. Заштрихуйте видимые грани куба (рис. 16), используя для каждой грани свой цвет.
Проекционный чертеж – это уже условное изображение, которое надо уметь читать. Учитель фиксирует внимание учащихся на том, что у видимой грани все ребра являются также видимыми. Учащиеся последовательно выделяют контуры, ограниченные сплошными («видимыми») линиями. Перед их взорами появляется куб с тремя видимыми гранями разного цвета.
2.3.3. Графические действия
Графические действия представляют собой операции по созданию графических изображений геометрических объектов.
Графика (греч.γραφικος — письменный, от греч. γραφω — пишу) — вид изобразительного искусства, использующий в качестве основных изобразительных средств линии, штрихи и пятна.
Графические действия различаются по использованию чертежных инструментов, по способу их задания, по использованию клетчатой или нелинованной бумаги. Эти действия составляют основное содержание задач, целью которых является:
- выполнение схематического рисунка, изображения фигуры от руки;
- построение с помощью инструментов фигуры или конфигурации по заданному алгоритму;
- воспроизведение заданного изображения;
- построение с помощью инструментов изображения по описанию.
Построить схематический рисунок к задаче, качественно отобразив в нем основные конструктивные особенности конфигурации, зафиксировать в графической форме мысленно созданный образ — важное умение, необходимое при решении геометрической задачи. А для этого учащиеся должны научиться выполнять изображения от руки. При этом учащиеся 5—6-х классов уже способны не просто копировать данные им изображения, а выполнять более сложные действия, например, преобразовать рисунок в проекционное изображение или перенести на бумагу созданный мысленный образ.[Приложение 1]
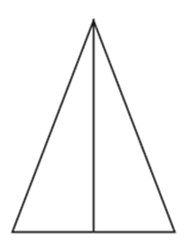
Пример 11. Нарисуйте от руки фигуру, симметричную данной относительно проведенной прямой (рис.17).

На основе данного изображения и представления об осевой симметрии учащиеся должны создать образ симметричной «птички» и постараться как можно точнее отобразить его на листе бумаги. Проверять правильность действий здесь необходимо уже по ходу их выполнения. Упражнение требует хорошо скоординированных движений.
Пример 12. Что можно сказать о взаимном расположении прямой и окружности, если расстояние от центра окружности до прямой равно 4 см, а радиус окружности равен 3 см? Сделайте схематический рисунок.
Выполнение схематического рисунка помогает учащимся «увидеть» описанную конфигурацию, если создание образа на основе описания вызвало затруднения. Учащиеся изображают окружность, проводят ее радиус, отмечают, что радиус равен 3 см. Далее они должны провести прямую; при этом понятно, что прямая, удаленная от центра окружности на 4 см, окружность не пересекает. Важно, чтобы прямая была проведена перпендикулярно радиусу с соблюдением масштаба.
Пример 13. На рисунке 18 изображен прозрачный цилиндр. Нарисуйте от руки цилиндр, проведя видимые линии сплошными, а невидимые — штриховыми.

Умение изобразить пространственное тело можно по праву отнести к практически важным.
Еще одно важное геометрическое умение — выполнять построения с помощью инструментов по заданному алгоритму, которые делятся на построения, выполняемые с использованием любых чертежных инструментов, и классические построения, выполняемые с помощью циркуля и линейки без делений.
Одна из причин затруднений в выполнении построений с помощью инструментов кроется в том, что у учащихся нет четкого представления о той последовательности действий, которая должна привести к желаемому результату. Поскольку действия эти, как правило, не фиксируются, ведь на рисунке в учебнике и предлагается конечный результат, который на самом деле возникает постепенно, в несколько шагов. Опытный учитель, выполняя построения на доске, все необходимые шаги, конечно, зафиксирует, а ученик, возможно, и повторит их у себя в тетради. Но запомнит ли? Сможет ли воспроизвести дома? Помочь учащимся выстроить алгоритм может последовательность рисунков стоп-кадров: изображений, последовательно фиксирующих отдельные, наиболее характерные моменты построения конфигурации. Последовательность рисунков содержит, как правило, кроме начальной и конечной конфигураций, одну-две промежуточные; каждая следующая конфигурация включает в себя предыдущую. Здесь необычайно важно, что рисунки дают учащимся возможность контролировать в ходе работы правильность выполняемых ими действий.
Последовательность рисунков должна быть подкреплена вербальным описанием производимых действий, зафиксированных рисунками. Описание может включать необходимые, для упрощения восприятия, пояснения, логические ссылки, другие возможные варианты построения.
Пример 14. Учащиеся должны изучить алгоритм построения касательной к окружности, параллельной данной прямой, и выполнить построения. Им предлагается прочесть описание построения, рассматривая по ходу чтения соответствующий рисунок:
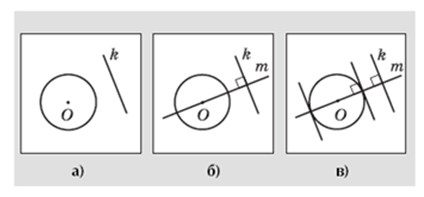
«Пусть дана окружность с центром в точке О и прямая k (рис. 19,а). Построим касательные к окружности, параллельные данной прямой. Для этого нужно:
1) провести через центр окружности прямую, перпендикулярную прямой k (на рис. 19,б эта прямая обозначена буквой m);
2) провести через точки пересечения прямой m с окружностью прямые, параллельные k (или перпендикулярные m) (рис. 19,в)».
Если учащийся из прочитанного текста не до конца уяснил описанное действие, он может сравнить предыдущий рисунок с тем, на котором изображен результат выполнения этого действия, и на основе анализа вычленить произошедшие изменения.
Особенностью этого задания является существование двух вариантов выполнения последнего действия: провести через точки пересечения прямой m с окружностью прямые, параллельные k, или прямые, перпендикулярные m. Учащиеся находят этому объяснение, а затем при построении выбирают одну из возможностей — по своему усмотрению.
Выполнение классических геометрических построений — выполняемых с помощью циркуля и линейки без делений — более характерно для курса планиметрии, т.к. вряд ли их можно отнести к естественным, все они основаны на логически обоснованных геометрических фактах. Кроме того, и саму идею введения весьма искусственного ограничения на пользование лишь двумя названными инструментами учащиеся воспринять пока не могут. В 5—6-х классах полезна как раз противоположная постановка вопроса – задействовать разные инструменты, придумывать разные алгоритмы и способы построения, активно используя при этом полученные знания о свойствах фигур и развивая
фантазию. При этом основой для многих построений, выполняемых циркулем и линейкой, служит конфигурация, образуемая двумя пересекающимися окружностями. Это построения треугольника по трем сторонам, серединного перпендикуляра к отрезку; точки, симметричной данной относительно прямой. Вот как выглядит алгоритм построения треугольника с заданными сторонами (рис. 20).
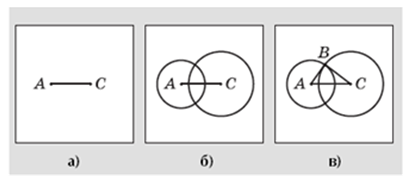
Задачу воспроизведения заданного изображения полезно решать как на клетчатой, так и на нелинованной бумаге. Эта задача требует от учащихся самостоятельно создать алгоритм построения заданной конфигурации на основе ее анализа. Клетчатая бумага, обладая мерной сеткой, параллельностью и перпендикулярностью линий, ее образующих, служит основой для определения особенностей конфигурации, подходов к ее воспроизведению, задает числовые характеристики составляющих элементов. Нелинованная бумага не содержит таких явных подсказок и требует более внимательного изучения заданного рисунка.
Черезтакого рода задачи учащиеся могут получить представление о новых способах построения известных им геометрических фигур. Например, воспроизводя конфигурацию «прямоугольник, вписанный в окружность», и увидев, что диаметры окружности являются диагоналями прямоугольника, учащиеся могут осознать, что начертить прямоугольник можно так: провести окружность и в ней два диаметра, после чего последовательно соединить их концы.
Пример 15. Скопируйте отрезок в тетрадь (рис.21).
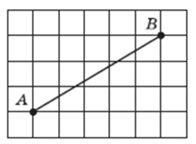
Выполняя это упражнение, учащиеся должны научиться «ходить» от узла к узлу не только по линиям сетки. Учащиеся определяют «путь» от точки А до точки В следующим образом: отсчитывают от точки А пять клеток вправо и три клетки вверх.
Освоенный прием может использоваться в дальнейшем при воспроизведении различных фигур. Может использоваться и учителем, например, чтобы «продиктовать» классу необходимый для дальнейшей работы треугольник.
Пример 16.Скопируйте в тетрадь фигуру, составленную из окружности и частей окружности (рис. 22).
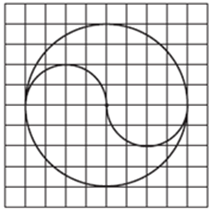
В этом задании клетчатая бумага используется в качестве измерительного инструмента. Учащиеся последовательно определяют, что конфигурация состоит из окружности и двух полуокружностей; радиус большой окружности равен четырем клеточкам, радиусы меньших окружностей — двум клеточкам; центры окружностей расположены на одной прямой; центры меньших окружностей расположены слева и справа от центра большой окружности на расстоянии, равном двум клеточкам.
Пример 17. Постройте такой же «цветок», как на рисунке 23.
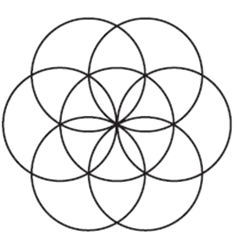
Рисунок задан на нелинованной бумаге, поэтому учащиеся могут выбирать числовые данные по своему усмотрению или произвести измерения на рисунке. Сначала они должны увидеть «серединку цветка» и шесть окружностей, образующих его «лепестки». Затем, сравнивая центральную окружность с одним из «лепестков», учащиеся устанавливают их равенство и особенности взаимного расположения — центр «лепестка» расположен на центральной окружности. На этом этапе можно начать выполнять построения: учащиеся проводят центральную окружность и строят один из «лепестков». Далее они снова возвращаются к анализу рисунка и определяют, что центром соседнего «лепестка» является точка пересечения центральной окружности и построенного «лепестка». Аналогичным образом строятся и остальные окружности.
Наибольшие трудности среди всех задач на построение представляет построение изображения по описанию, так как это предполагает создание сначала зрительного образа на основе вербального описания, а затем способа его построения. Здесь поможет такой прием, как достраивание изображения на готовом чертеже, которые, как правило, даются в рабочих тетрадях.
Пример 18. Отрезки АВ и АС — стороны четырехугольника АВОС (рис.24). Известно, что угол С равен 90 °, а сторона ВО параллельна стороне АС. Достройте этот четырехугольник.
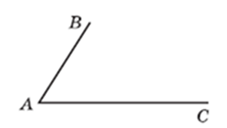
Результатом построений является прямоугольная трапеция, самостоятельное построение которой по описанию вызвало бы у учащихся серьезные затруднения.
2.3.4.Конструирование
Под детским конструированием принято подразумевать создание разных конструкций и моделей из строительного материала и деталей конструкторов, изготовление поделок. Говоря о конструировании, будем иметь в виду создание предметных моделей геометрических объектов. Эти действия естественным образом реализуются через задачи:
- на пространственное моделирование;
- на построение фигуры с помощью перегибания листа бумаги;
- на разрезание и складывание.
Выбор именно этих видов моделирования определяется их доступностью для использования на уроке и дома, наличием у учащихся необходимых навыков, однако учителя активно используют, например, и такой вид математического конструирования, как оригами.
Вопросу использования оригами в учебном процессе посвящены публикации различных авторов:
Перегибание листа бумаги является для учащихся операцией, знакомой по выполнению различных поделок из бумаги. Однако, повторяя за учителем последовательность требуемых от него действий, учащийся не осознает их геометрической сущности. Здесь ему предлагается решить геометрическую задачу, но путем перегибания и привлекая имеющиеся геометрические знания.[Приложение 2]
Пример 19. Перегибая лист бумаги, постройте ромб.
Построение основано на свойстве диагоналей ромба и равенстве его сторон. Учащиеся дважды перегибают лист так, чтобы образовался прямой угол, а затем загибают его. Развернув лист, они обводят карандашом линии сгиба, образующие ромб.
Пространственное моделирование выполняет часто вспомогательную функцию изготовления моделей пространственных тел, необходимых в процессе изучения их свойств. Например, для изучения свойств симметрии в пространстве каждому учащемуся необходимо вылепить из пластилина модели шара, конуса, цилиндра, куба. Эти модели помогают при изучении сечений пространственных тел. При изучении развертки куба и для овладения навыками оперирования мысленными образами учащиеся должны иметь несколько фигур, из которых можно свернуть куб и из которых куб свернуть нельзя. Они изготавливают их самостоятельно по данным им разверткам и рисункам. Помимо этого, учащиеся решают и собственно конструктивные задачи, где им нужно, опираясь на мысленный образ моделируемого тела, выделить особенности конструкции, задать самостоятельно или определить его размеры, изготовить развертку. Вот примеры таких заданий.
Пример 20. Изготовьте из картона куб объемом 1 дм3.
Пример 21. Модель треугольной пирамиды можно сделать из трубочек, например, для коктейля (рис.25). Соединить трубочки можно, продев внутрь нить или тонкую проволоку. Возьмите необходимое количество трубочек одинаковой длины и сделайте из них модель треугольной пирамиды.

Разрезание и складывание фигур служит развитию и углублению представлений о геометрических фигурах, обнаружению существующих между ними связей. Так, квадрат можно разрезать на два равных прямоугольника (по оси симметрии, перпендикулярной сторонам квадрата), на два равных прямоугольных равнобедренных треугольника (по одной диагонали), на четыре равных квадрата и т.п.
Пример 22. Возьмите квадрат и разрежьте его по диагоналям. Сложите из получившихся фигур прямоугольник.
Пример 23. Возьмите прямоугольник, одна из сторон которого вдвое больше другой. Разрежьте его на две части так, чтобы из них можно было составить равнобедренный треугольник.
Ценность полученных навыков заключается в том, что в дальнейшем разрезание и достраивание используется в качестве приема: на основе действий по перекраиванию можно находить площади параллелограмма и треугольника; составление паркетов из равных треугольников позволяет «увидеть», что сумма углов треугольника равна 180° и пр.
Пример 24. Вырежьте из листа бумаги параллелограмм и перекроите его в прямоугольник. Чему равна площадь параллелограмма?
Можно использовать в учебных целях и такую хорошо известную игру-головоломку, как «Танграм».
2.3.5.Действия измерения
Действия измерения состоят из операций по измерению геометрических величин и усвоению эталонов длины, площади, объема и градусной меры угла. Используются они в ходе выполнения упражнений, требующих:
- выполнения измерений с помощью инструментов;
- выбора и преобразования единиц измерения;
- измерения величины на глаз;
- сопоставления величин непосредственно воспринимаемых объектов;
- выполнения вычислений геометрических величин.
Овладение практическими измерениями включает в себя осознание самого процесса измерения, знание устройства используемого измерительного инструмента, его шкалы, умение им пользоваться. Измерение длины отрезка знакомо учащимся из начальной школы, поэтому здесь необходимо, во-первых, уточнить, насколько осознанно учащиеся его выполняют, во-вторых, расширить круг применения, например, для измерения длины ломаной, произвольной кривой, расстояния между двумя точками, от точки до прямой, между двумя параллельными прямыми. Можно поговорить и об измерении расстояния от точки до фигуры. Полезны практические измерения, которые можно выполнять в классе: попросите учащихся измерить длину и ширину стола, высоту стула, размеры двери, найти расстояние между двумя столами, ширину прохода между рядами и пр. Аналогичные задания можно выполнить и при изучении площади. Все это естественным образом подходит для организации лабораторных или проектных работ, для использования групповых форм работы, которые так нравятся учащимся.
Пример 25. Проведите на листе нелинованной бумаги две параллельные прямые и найдите расстояние между ними.
В этом задании выполнению измерений предшествует дополнительное построение прямой, перпендикулярной двум проведенным прямым. Кроме того, учащиеся должны понимать, что расстояние между двумя параллельными прямыми есть длина отрезка перпендикулярной прямой, заключенного между ними.
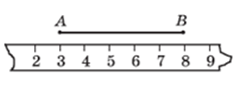
Пример 26. По рисунку 26 определите длину отрезка АВ.
В данном случае способность найти выход из нестандартной ситуации говорит о понимании сути процесса измерения.
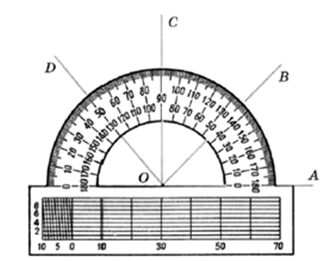
В отличие от измерения длины отрезка, измерение величины угла — новый вид измерений. Помочь учащимся им овладеть призваны задания, которые выполняются на изображениях транспортира (рис. 18).
В них учащимся не надо для измерения угла прикладывать транспортир, это уже изображено на рисунке. Они должны выполнить только ту часть действий, которая включает определение величины угла по шкале. При этом они привыкают к правильному расположению транспортира, их внимание фиксируется на том, какой шкалой удобно пользоваться. Первые построения угла заданной градусной меры также полезно осуществлять на рисунках, где дано изображение транспортира и проведена одна из сторон угла (рис. 27).
Овладев навыками измерения, учащиеся имеют возможность использовать их для поиска геометрических закономерностей. Так, измерение углов треугольника подводит к «открытию» факта, что сумма углов любого треугольника равна 180°. Понятно, что это возможно только в том случае, если учащиеся выполняют измерения транспортиром не только правильно, но и достаточно точно.
Полезно использовать в качестве измерительного инструмента и циркуль — для откладывания равных отрезков или нахождения ближайшей точки прямой.
Овладение практическими измерениями невозможно без знания единиц измерения. Решение любой практической задачи включает выбор единиц измерения или преобразование заданных. Достаточно, чтобы учащиеся хорошо знали соотношения между линейными метрическими величинами и на их основе осуществляли преобразование единиц площади и объема.
Пример 27. В каких единицах измеряют: а) расстояние от дома до школы; б) длину отреза ткани при покупке; в) расстояние между городами; г) площадь квартиры?
Пример 28. Какие измерения надо провести, чтобы определить, какую примерно площадь занимает территория вашей школы? Сравните эти площади с 1 соткой и 1 гектаром. Задание полезно выполнить практически.
Научиться осознанно, не формально, преобразовывать единицы измерения можно только тогда, когда эти преобразования сначала выполнены практически. Можно предложить учащимся начертить квадрат со стороной 1дм и определить его площадь в квадратных дециметрах; затем разбить его на квадраты со стороной 1 см и подсчитать число квадратов. Они получили, что площадь квадрата равна 1 дм2 или 100 см2. Отсюда и следует зависимость между квадратным дециметром и квадратным сантиметром. Осознанные действия постепенно переходят во внутренний план, но в памяти остаются и могут быть повторены при необходимости.
Пример 29. Куб с ребром 1 м разрезали на кубики с ребром 1 см и выстроили в один ряд. Какой длины получился ряд?
Это пример сложного задания, требующего от учащихся свободного владения не только единицами длины и единицами объема, но и понимания сущности измерений. Выполняя его, более сильные учащиеся вполне могут рассуждать формально: в 1 м3 содержится 100 ∙100∙100 = 1003 = 1000000см3, значит, столько и будет кубиков длиной 1 см; а длина ряда равна 1 000 000 см = 10 000 м = 10 км. Тот, кто не готов к формальным действиям, может использовать воображение и разрезать куб мысленно, сначала на слои, а затем выстраивая каждый слой в один ряд.
Измерение величины на глаз является достаточно важным практическим умением, которое часто оказывается востребованным в жизни. А умение определить, что выполненное изображение не соответствует условию задачи, полезно при изучении геометрии. Это становится возможным только в случае сформированности мысленных эталонов меры, поэтому задачи такого рода можно ставить перед учащимися тогда, когда они уже освоились с основными понятиями, приобрели некоторые навыки построения и измерения, накопили необходимые зрительные образы. Основная цель овладения умением оценивать геометрические величины на глаз — использование этого умения для самоконтроля над выполненными действиями, для анализа достоверности зрительной информации.
Пример 30. На рисунке 28 изображен угол. Учащиеся должны определить величину этого угла на глаз.
Какие действия необходимо для этого выполнить? 1) Мысленно сравнить данный угол с прямым углом; 2) сравнить его с половиной прямого угла; 3) например, данный угол меньше угла в 90°, но больше угла в 45°; необходимо определить, к какому из этих двух углов ближе его градусная мера и прикинуть величину этой разницы; 4) прибавить или отнять величину разницы от ближайшего эталона (в данном случае эталонами служат углы в 90° и 45°). Неоднократное выполнение описанных действий постепенно приводит к формированию нового эталона — угла в 60°.
Однако нельзя научиться оценивать геометрические величины на глаз, если не было опыта сопоставления величин непосредственно воспринимаемых объектов. Так, выполнению предыдущего упражнения, рассмотренного в примере 30, как легко понять, предшествует непосредственное сравнение различных углов с прямым углом, с углом в 45°.
Пример 31. Вырежьте из листа бумаги квадрат со стороной 1 дм. Используя его в качестве эталона, определите на глаз площадь тетрадного листа, поверхности стола.
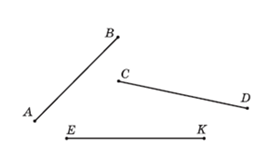
Пример 32. Назовите отрезки в порядке возрастания их длин (рис.29).
Пример 33. Какие отрезки можно закрыть кругом (рис. 29)?
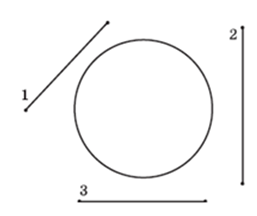
Сравнивать различные геометрические объекты приходится при решении многих задач, например, внимательное сравнение изображений двух аквариумов из примера 34 позволяет найти более рациональное и красивое решение.
Пример 34. Из двух одинаковых листов стекла вырезают заготовки для двух аквариумов, изображенных на рисунке. В каком случае площадь обрезков будет больше?
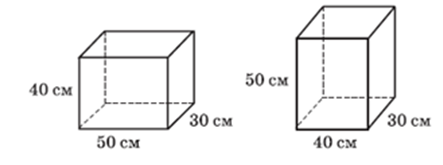
Это решение основывается на том, что аквариумы представляют собой один и тот же параллелепипед, с одной отсутствующей гранью. Значит, чтобы ответить на вопрос задачи, надо сравнить площади этих отсутствующих граней. Там, где площадь грани меньше, площадь обрезков будет больше. Интересно оно и последним логическим ходом.
При решении задач на вычисление геометрических величин выделяются три аспекта: владение понятиями, формальными правилами вычисления и свойством аддитивности.
Новым понятием для учащихся 5—6-х классов является понятие объема, с понятием площади они уже знакомы. Целесообразно первоначально геометрические величины находить в абстрактных единицах — ввести понятия единицы длины, квадратной единицы, кубической единицы; фигуры разбиваются на квадраты, площади которых приняты за 1 кв. ед., а уже затем осуществляется переход к метрическим единицам.
Пример 35. Объем каждого кубика равен 1 куб. ед. Чему равен объем тела (рис. 31)?
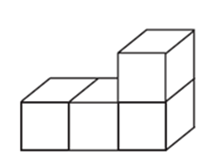
Пример 36. Нарисуйте фигуру той же площади, что и фигура, изображенная на рисунке 32.
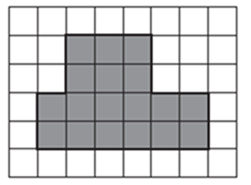
Необходимо учитывать, что неоправданно быстрый переход к формальному правилу (вычисление площади прямоугольника, объема параллелепипеда) приводит часто к его отрыву от усвоенного понятия и затрудняет практическое применение. Этот переходный этап должен быть обеспечен адекватным содержанием. Например, такими заданиями:
Пример 37. Начертите в тетради прямоугольник со сторонами 6 см и 8 см. Разбейте прямоугольник на квадраты со стороной 1 см и определите его площадь.
Учитель предлагает учащимся закрасить один из квадратов площадью 1 см2. Важно, чтобы учащиеся считали квадраты сначала одного ряда, а затем считали число рядов. Учитель еще раз обращает внимание учащихся на то, что число квадратов в ряду равно длине одной из сторон прямоугольника, а число рядов — длине другой стороны. И здесь не приходится рассчитывать на то, что понятие площади и правило вычисления площади прямоугольника были сформированы в начальной школе. Это объективно трудный материал, и не надо требовать от учащихся невозможного.
Пример 38. Постройте на нелинованной бумаге прямоугольник, выполните необходимые измерения и вычислите его площадь.
Это задание усложняется тем, что вряд ли длины сторон построенного прямоугольника будут выражаться «хорошими» — круглыми числами, что привычно, скорее всего, в результате выполненных измерений учащиеся получат что-то вроде 5 см 3 мм, значит, им придется выражать длины сторон в миллиметрах, а затем находить произведение двузначных чисел. Это именно тот тип заданий, перед которым наши учащиеся, как показывают результаты международных исследований, пасуют.
Пример 40. Определите площадь фигуры (рис. 33).
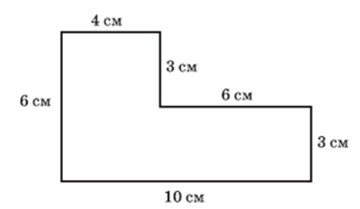
При решении этой задачи целесообразно подвести учащихся к осознанию двух способов решения: первый — путем разрезания исходной фигуры на два прямоугольника, второй — путем ее достраивания до прямоугольника.
Завершая разговор о действиях, составляющих геометрическую деятельность, следует сказать о том, что отнесение той или иной задачи к определенной группе является достаточно условным. Понятно, что ее выполнение только в редких случаях основано, например, только на действиях восприятия, чаще оно требует совместной работы восприятия, воображения и мышления и, соответственно, выполнения различных действий.»
